|
|
В) Решить данную систему методом обратной матрицы.МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ имени К.Г. РАЗУМОВСКОГО (Первый казачий университет)» (ФГБОУ ВО «МГУТУ им. К.Г. Разумовского (ПКУ)») Башкирский институт технологий и управления (филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Московский государственный университет технологий и управления имени К.Г. Разумовского (Первый казачий университет)» БИТУ (филиал) ФГБОУ ВО «МГУТУ им. К.Г. Разумовского (ПКУ)»
МАТЕМАТИКА Методические рекомендации по выполнению контрольных работ для бакалавриата очно- заочной формы обучения
38.03.07 по направлению Товароведение
1. РАБОЧАЯ ПРОГРАММА КУРСА Элементы линейной алгебры. 1. Матрицы. Виды матриц. Действия над матрицами, свойства матриц. Обратная матрица. Определители, их свойства. Вычисление определителей. 2. Системы линейных уравнений. Метод Гаусса, правило Крамера. Ранг матрицы, теорема Кронекера - Капелли. Квадратичные формы. 3. Понятие о задаче линейного программирования и симплекс – методе. Элементы векторной алгебры и аналитическая геометрия плоскости. 1. Системы координат на плоскости. Векторы. Линейные операции над векторами. Линейная зависимость векторов. Базис, координаты вектора в данном базисе. Скалярное произведение векторов. Уравнения прямых на плоскости. Кривые второго порядка.
Введение в математический анализ 1.1. Переменные и постоянные величины. Функции: область определения, способы задания функции. Предел функции. Основные теоремы о пределах (суммы, произведения, частного). Первый и второй замечательные пределы. Число е. Натуральные логарифмы. 1.2. Непрерывность функции. Односторонние пределы функции в точке. Точки разрыва функции и их классификация. Непрерывность функции. Дифференциальное исчисление функции одной переменной 2.l. Производная функции, её геометрический, механический смысл, свойства. Производная сложной функции. Производная обратной функции. Таблица производных. 2.2. Дифференциал функции, его геометрический смысл. Применение дифференциала в приближённых вычислениях. 2.3. Теоремы Ролля, Лагранжа, Коши. Раскрытие неопределённостей, правило Лопиталя. 2.4. Формулы Тейлора и Маклорена, их применение к приближённым вычислениям. 2.5. Исследование функций. Точки экстремума. Необходимые и достаточные условия максимума и минимума. Выпуклость и вогнутость. Асимптоты кривых. Общая схема исследования функции и построение графиков. Основы интегрального исчисления 3.1. Задачи, приводящие к понятию неопределённого интеграла. Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов. Интегрирование методом замены переменной и по частям. Другие приёмы интегрирования. 3.2. Задачи, приводящие к понятию определённого интеграла. Формулировка теоремы о его существовании. Свойства определенного интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Вычисление неопределённого интеграла с помощью интегрирования по частям и замены переменной. 3.3. Несобственные интегралы с бесконечными пределами, с неограниченной подынтегральной функцией. 3.4. Приложения определенного интеграла.
УЧЕБНАЯ ЛИТЕРАТУРА А) Основная. 1. Шипачев В.С. Высшая математика: Учеб. Для вузов/ В.С. Шипачев. – М.: Высш. Шк., 2006. – 479 с. 2. Шипачев В.С. Задачник по высшей математике: Учеб. Пособие для вузов/ В.С. Шипачев. – М.: Высш. Шк., 2003. – 304 с. 3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И. Ермакова. – М.: ИНФРА-М, 2006. – 575 с. 4. Практикум по высшей математике для экономистов. Под ред. проф. Н.Ш. Кремера.- М.: ЮНИТИ-ДАНА, 2005. – 423 с.
Б) Дополнительная 1. Баврин И.И. Курс высшей математики. Учебник. – М., Просвещение, 1992. 2. Беклемишева Л.А., Петрович Ю.А., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. – М., Наука, 1987. 3. Кузнецов Л.А. Сборник задач по высшей математике. - М., Высшая школа, 1991 (уч. пособие). 4. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М., Наука, 1984. 5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики.- М., 1985. 6. Бугров Я.С., Никольский С.М. Высшая математика. Задачник. – М., Наука, 1982. 7. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Ч.1, - М., Финансы и статистика, 1998.
Методические указания к решению задач Для того, чтобы облегчить студенту-заочнику самостоятельное выполнение контрольных работ, приведем примеры решений задач, аналогичных тем, какие предлагаются в контрольных работах. Подобные задачи включаются и в экзаменационные билеты.
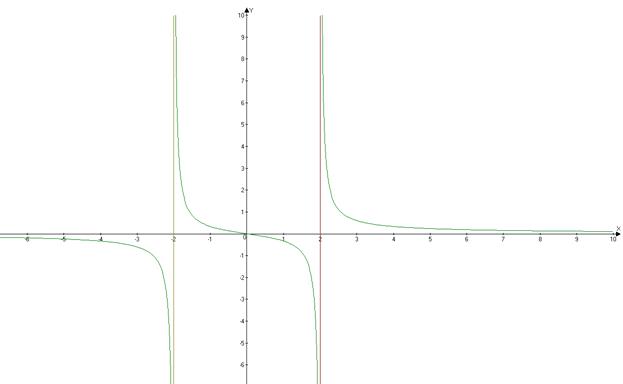
Задача из раздела I Задача 1.Дана система линейных уравнений
Требуется показать, что система совместна, и найти ее решение тремя способами: а) по формулам Крамера; б) методом Гаусса; в) методом обратной матрицы. Выполнить проверку решения. Решение. Система n линейных уравнений с n неизвестными является совместной и имеет единственное решение, так как определитель системы, составленный из коэффициентов при неизвестных не равен нулю. Вычислим определитель системы методом разложения его по элементом строки. Разложим по первой строке:
Так как определитель системы не равен нулю, система уравнений совместна и имеет единственное решение. а) Найдем решение системы по формулам Крамера
где D1 D2 D3 - определители, которые получаются из определителя D системы путем замены в нем соответственно 1-го, 2-го, 3-го столбцов коэффициентов при неизвестных x1 x2 x3 столбцом свободных членов уравнений, стоящих в правой части данной системы. Получим следующие три определителя:
Вычислить неизвестные Проверим это решение, подставив значения неизвестных во все уравнения системы. Получим
б) Решим ту же систему уравнений методом Гаусса. Для этого выпишем расширенную матрицу системы и приведем основную матрицу системы к треугольному виду или ступенчатому виду, если число уравнений окажется меньшим числа неизвестных. Приведение матрицы к треугольному виду, то есть такому, когда ниже (или выше) главной диагонали все элементы будут нулевые, а на главной диагонали - ненулевые, всегда возможно. Оно основано на следующих элементарных преобразованиях матрицы, соответствующих эквивалентным преобразованиям система: 1. Перестановка строк матрицы; 2. Перестановка столбцов; 3. Умножение всех элементов строки на одно и то же число; 4. Сложение элементов любой строки с соответствующими элементами любой другой строки; 5. Вычеркивание получившихся нулевых строк. Вот решение одной системы методом последовательных исключений неизвестных: Расширенная матрица 1-й шаг 2-шаг
Возвратимся теперь от матричной записи к системе уравнений. Из последней строки матрицы следует уравнение Существует модифицированный метод Гаусса, так называемый метод полного исключения неизвестных, в результате которого основная матрица системы преобразуется в каноническую матрицу, на главной диагонали которой остаются единицы, а все остальные элементы обращаются в нули. Таким образом сразу получается решение. В основе этого метода лежит следующий алгоритм (строго определенный порядок действий) 1. Выберем разрешающую строку и в ней разрешающий элемент. Обычно это первый элемент первой строки, считая слева направо. Строки можно целиком переставлять, так что на первое место можно записать любую строку, в которой первый элемент не равен нулю. 2. Каждый элемент, разрешающий строки разделим на разрешающий элемент. 3. Элементы разрешающего столбца заменим нулями во всех строках матрицы, кроме разрешающей, где он буден равен единице. 4. Элементы столбцов, Которые были разрешающими на предыдущих шагах исключения, переписываем без изменения. 5. Остальные элементы пересчитаем по следующему правилу «прямоугольника»:
Где П – пересчитываемый элемент, Р – Разрешающий, D1 и D2 – “диагональные”, И – искомый. Все эти элементы каждый раз должны быть вершинами воображаемого прямоугольника, образованного параллельными строками и столбцами. Искомый элемент записываем на месте пересчитываемого. Вернемся к расширенной матрице данной системы и выполним эквивалентной преобразования по предложенной выше схеме полного исключения неизвестных. Рекомендуем читателю все пересчеты коэффициентов по правилу «четырехугольника» записывать подробно.
Данная расширенная матрица 1-й шаг 2-й шаг
3 - й шаг 4 – й шаг
Если в последней матрице вернуться к записи уравнений, то получим
Замечания: 1. Кружками обведены разрешающие элементы. 2. При переходе от 2-го шага к 3-му третью строку почленно разделили на 90/7. в) Решить данную систему методом обратной матрицы. Решение. Данную систему можно записать в матричном виде АХ = В, где Решение матричного уравнения имеет вид Х = А-1 В = N, где А-1 – матрица, обратная матрицы А. Так как определитель матрицы системы D(A) = 180 отличен от нуля то матрица А имеет обратную. Для вычисления обратной матрицы воспользуемся формулой
Где А11, А12, …, А33 – алгебраические дополнения элементов а11, а12, …, а33 матрицы А. Вычислим алгебраические дополнения всех элементов матрицы А:
Составим обратную матрицу
Найдем теперь матрицу Х.
Из равенства матриц Х = N или х1=2, х2 = 1, х3 = -3. Задача 2. Методом исключения неизвестных найти общее и базисное решение системы линейных уравнений Решение.
Это система двух уравнений с тремя неизвестными. Она совместна и неопределенна. Надо описать совокупность всех ее решений. В качестве базисных неизвестных данной системы можно взять те неизвестные, для которых определитель составленный из коэффициентов при нет известных, не равен нулю. Здесь три таких определителя, один из которых равен нулю Или в матричной форме Общее решение: Полагая в общем решении х3 = 0, получим базисное решение х1 = Проверка базисного решения показывает, что оно удовлетворяет обоим уравнениям системы, то есть, является частным решением системы. Давая х3 любые другие числовые значения, получим бесчисленное множество частных решений. Аналогично решаются системы с несколькими свободными неизвестными. Задача 3.Даны матрицы произведение матриц АВ. Решение. Эти матрицы являются соответственными, так как число столбцов первой матрицы равно числу строк второй: их размеры
Задачи раздела ΙΙ Задача 1.Даны вершины треугольника А(-3;-2), В(1;8), С(5;3). Найти: а) уравнения всех трех его сторон; б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны; в) внутренний угол А треугольника в градусах и минусах; г) длину высоты, опущенной из вершины А; д) площадь треугольника. Решение. а)Уравнения сторон найдем по формуле прямой, проходящей через две данные точки Уравнение стороны АВ:
Уравнение стороны АС:
б)Каждая из прямых, уравнения которых только это найдены, разделяет плоскость на две полуплоскости, определяемые соответствующими неравенствами.
Рис. 1.
Система неравенств в)Внутренний угол треугольника найдем, зная угловые коэффициенты сторон АВ и АС, образующих этот угол, по формуле Угловые коэффициенты прямых выложим по формуле Получим Тогда
г)Длину высоты AD^BC (рис. 1) найдем как расстояние от данной точки А(-3;-2) до данной прямой ВС: 5х + 4у – 37 = 0 по формуле
Получим
д)Площадь треугольника можно вычислить несколькими способами. Вычислить ее через координаты вершин треугольника по формуле Получим Итак, площадь треугольника SABC = 30 кв. ед. Задача 2.Даны векторы a) длину вектора b) скалярное произведение векторов c) косинус угла между векторами d) смешанное произведение векторов e) объем параллелепипеда Решение: a) b) c) d) e) Задачи из раздела Дифференциальное и интегральное исчисление Задача 1. Вычислить пределы данных функций. а) Решение:
б) Решение:
в) Решение:
г) Решение:
Задание 2. Найти производные функций: а) Решение:
б) Решение:
в) Решение:
г) Решение:
Задача 3.Исследовать функцию методами дифференциального исчисления и построить график.
Решение: 1) Область определения.
2) Область непрерывности. Т.к. данная функция элементарная, то ее область определения совпадает с областью непрерывности, т.е. x=-2, Исследуем характер точек разрыва.
x=-2 - точка разрыва второго рода.
x=2 - точка разрыва второго рода. 3) найдем асимптоты графика функции.
y=0 - горизонтальная асимптота графика функции. 4) найдем точки пересечения с осями координат. С осью ОХ: y=0, значит, (0;0) – точка пересечения с осью ОХ. С осью OY: x=0, значит, (0;0) – точка пересечения с осью ОY. 5) четность, нечетность функции.
Значит, данная функция является нечетной, следовательно, график функции симметричен начала координат. 6) найдем экстремумы функции, интервалы возрастания, убывания функции.
Следовательно,
Функция убывает при Точек экстремума нет. 7) найдем точки перегиба и интервалы выпуклости, вогнутости графика функции.
Следовательно,
График функции выпуклый при (0;0) точка перегиба. 8) построим график функции.
Задача 3. Найти неопределенный интеграл. а) Решение:
б) Решение:
в) Решение:
г) Решение:
Задача 4. Вычислить несобственные интегралы или доказать их расходимость. а) Решение:
Значит, интеграл сходится и равен б) Решение:
Задача 5. Вычислить площадь фигуры, ограниченной линиями.
Решение: Найдем точки пересечения кривых.
(0,5), (4,29) – точки пересечения.
Как видно из рисунка данная фигура ограничена слева прямой Следовательно,
|
|

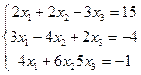
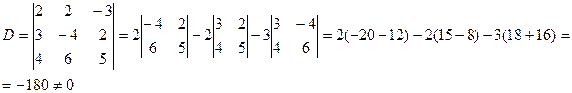
 ,
,  ,
,  ,
,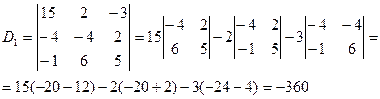

 ,
,  ,
,  .
. Решение верное.
Решение верное.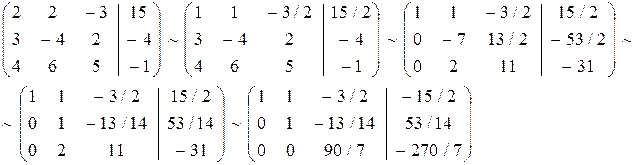
 , откуда х3 = -3 Подставляя х3 = -3 в последнее уравнение (вторая строка расширенной матрицы) получим
, откуда х3 = -3 Подставляя х3 = -3 в последнее уравнение (вторая строка расширенной матрицы) получим  или
или  . Наконец, из первого уравнения системы (первая строка матрицы) найдем
. Наконец, из первого уравнения системы (первая строка матрицы) найдем  Решение
Решение  такое же , как в случае (а). Оно уже проверено.
такое же , как в случае (а). Оно уже проверено.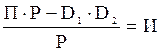

 РD2
D1 П
РD2
D1 П
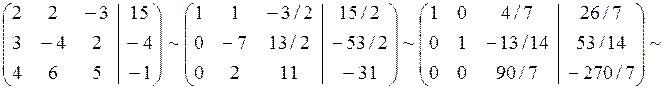
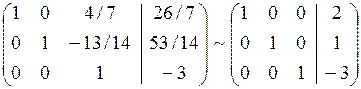
 ,
,  ,
,  , а это и есть решение данной системы.
, а это и есть решение данной системы. ,
,  ,
, 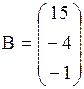
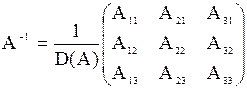
 ;
;  ;
;  ;
; ;
;  ;
; 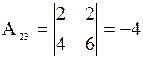
 ;
;  ;
;  .
.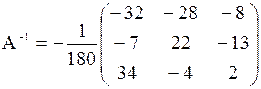 .
.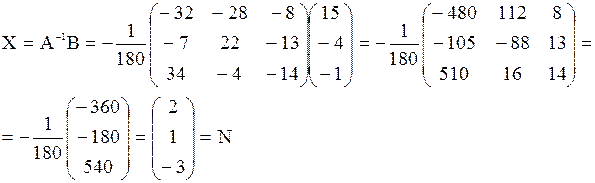
 следует решение системы
следует решение системы
 . Следовательно, неизвестные х1 и х2 нельзя брать в качестве базисных. Примем за базисные неизвестные х1 и х2 , для которых определитель
. Следовательно, неизвестные х1 и х2 нельзя брать в качестве базисных. Примем за базисные неизвестные х1 и х2 , для которых определитель  . Будем считать неизвестную х3 свободной и запишем систему в виде
. Будем считать неизвестную х3 свободной и запишем систему в виде 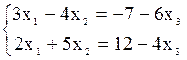
 . Воспользуемся методом полного исключения неизвестных:
. Воспользуемся методом полного исключения неизвестных: 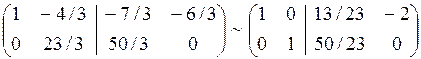
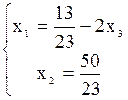
 ,
, 
 и
и  . Найти
. Найти и
и  . В результате умножения матриц получим новую матрицу С размера
. В результате умножения матриц получим новую матрицу С размера  , а ее элементы будут равны скалярным произведениям векторов-строк первой матрицы на векторы-столбцов второй:
, а ее элементы будут равны скалярным произведениям векторов-строк первой матрицы на векторы-столбцов второй: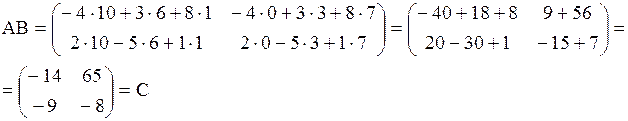
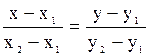
 , или
, или  (АВ).
(АВ). или
или  (АС)
(АС)






 Чтобы определить знаки этих неравенств, возьмем координаты какой-нибудь точки заведомо расположенной внутри треугольника АВС (см. рисунок 1). Такой точкой является, например точка N (0;1) подставляя координаты этой точки в уравнения граничных прямых (сторон) в силу того, что точка N не лежит ни на одной сторон, получим следующую систему неравенств.
Чтобы определить знаки этих неравенств, возьмем координаты какой-нибудь точки заведомо расположенной внутри треугольника АВС (см. рисунок 1). Такой точкой является, например точка N (0;1) подставляя координаты этой точки в уравнения граничных прямых (сторон) в силу того, что точка N не лежит ни на одной сторон, получим следующую систему неравенств.  определяющих множество внутренних точек треугольника.
определяющих множество внутренних точек треугольника. определяет множество точек, принадлежащих треугольнику АВС, включая его стороны.
определяет множество точек, принадлежащих треугольнику АВС, включая его стороны.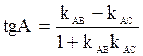 .
.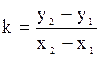 .
. ;
;  .
.
 . Угол определяем с помощью таблицы тангенсов или калькулятора
. Угол определяем с помощью таблицы тангенсов или калькулятора , где А, В, С – коэффициенты прямой,
, где А, В, С – коэффициенты прямой,  - координаты данной точки.
- координаты данной точки. (мин. ед.)
(мин. ед.) .
. .
. (1; 1; 1),
(1; 1; 1),  (2; 1; 4),
(2; 1; 4),  (3; -1; 1) Найти:
(3; -1; 1) Найти: ;
;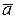 и
и 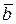 ;
; ;
; и объем пирамиды
и объем пирамиды  , построенных на векторах
, построенных на векторах  2
2  .
.
 .
. .
. .
.
 .
. .
. .
. .
. .
. .
.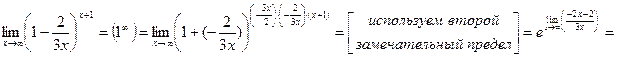
 .
. .
.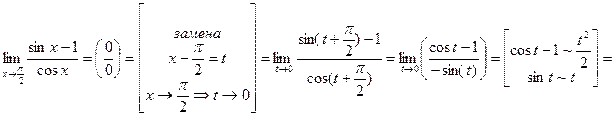
 .
. .
.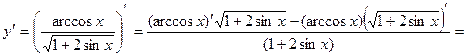

 .
. .
.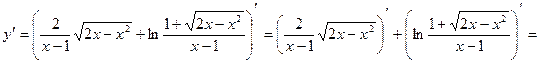
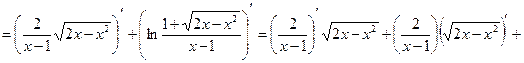
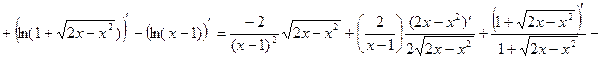
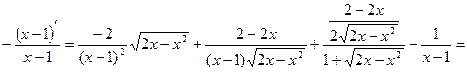
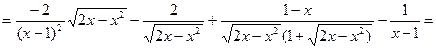
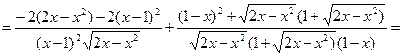
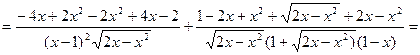
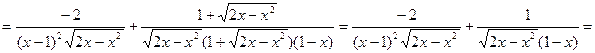
 .
. .
. .
. .
.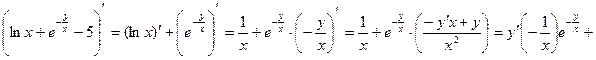
 .
. .
. .
. .
. .
. .
. .
. .
. , значит,
, значит,  - область определения.
- область определения. – точки разрыва.
– точки разрыва. .
. .
. .
. .
.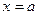 - вертикальная асимптота, если
- вертикальная асимптота, если  , следовательно, x=-2,
, следовательно, x=-2,  - наклонная асимптота (при
- наклонная асимптота (при  =0 горизонтальная), если существуют конечные пределы:
=0 горизонтальная), если существуют конечные пределы:  ,
,  .
. .
.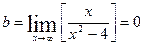
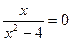 , x=0.
, x=0. .
. .
.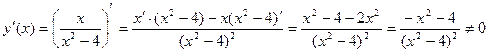
 - критические точки (
- критические точки (  не существует).
не существует).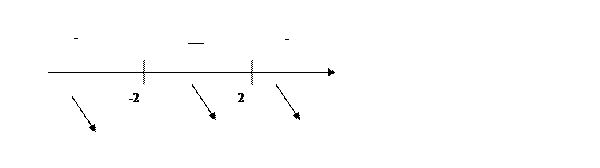
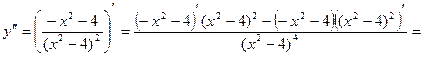
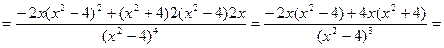
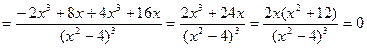
 - критическая точка (
- критическая точка (  =0).
=0). не существует).
не существует).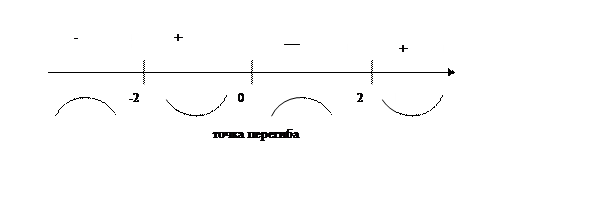
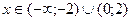 , график функции вогнутый при
, график функции вогнутый при  .
.
 .
. .
. .
.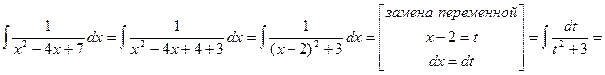
 .
. .
. .
.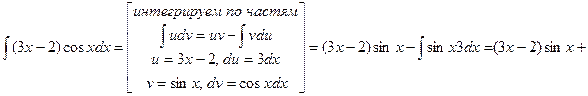
 .
. .
.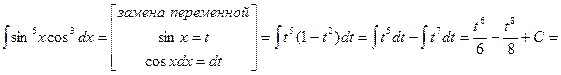
 .
. .
.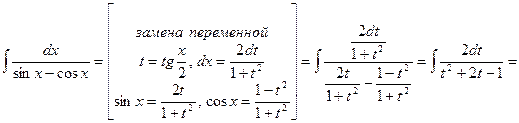

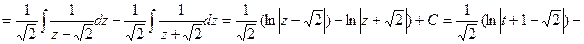
 .
. .
. .
.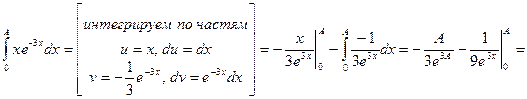
 .
. .
. .
.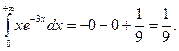
 .
. .
. .
.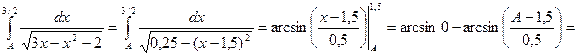
 .
. .
. .
. .
. - это парабола с вершиной в точке (0,5), ветви направлены вверх.
- это парабола с вершиной в точке (0,5), ветви направлены вверх. - это прямая линия. Сделаем чертеж.
- это прямая линия. Сделаем чертеж.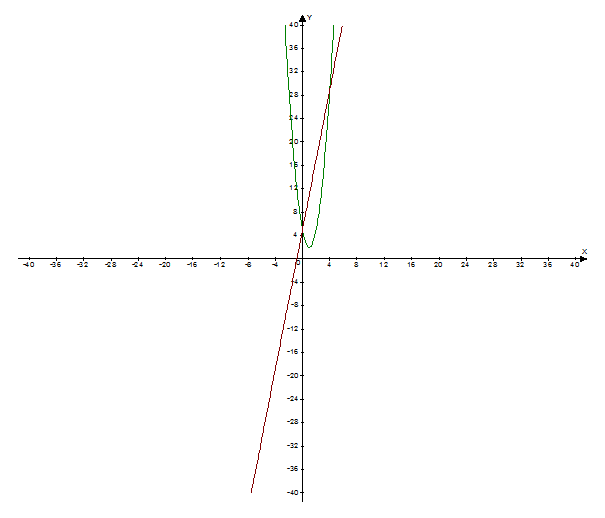
 , сверху прямой
, сверху прямой  (кв.ед.).
(кв.ед.).