|
|
Коэффициенты разложения нагрузки в ряд по синусам кратного аргумента.УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ Во многих приложениях приходится иметь дело с дифференциальным уравнением, которое в случае двух независимых переменных имеет вид
где А, В, С - функции от x и у. Особенно важен случай, когда f линейно относительно ω, ∂ω/∂x, ∂ω/∂y; в этом случае уравнение называется линейным. Характеристиками уравнения называются интегральные кривые обыкновенного дифференциального уравнения
Могут иметь место три случая: В2-АС>0 - уравнение имеет два семейства действительных характеристик и называется уравнением гиперболического типа; В2-АС-0 - уравнение имеет одно семейство действительных характеристик и называется уравнением параболического типа; В2-АС<0 - уравнение не имеет действительных характеристик и называется уравнением эллиптического типа. Если общие интегралы дифференциального уравнения характеристик имеют вид φ(х, у)=u, ψ(x, y)=v, то, приняв u и v за новые независимые переменные, можно привести уравнение к каноническому виду: для уравнения гиперболического типа
для уравнения параболического типа
для уравнения эллиптического типа
здесь
Особенно часто встречаются следующие частные случаи рассматриваемого здесь дифференциального уравнения второго порядка: Уравнение распространения колебаний в однородной среде
Уравнение теплопроводности
Уравнение распространения электрического тока по проводу
Уравнение теории потенциала
(уравнение Пуассона). При ρ=0 это уравнение называется уравнением Лапласа, или гармоническим уравнением. Часто приходится встречаться также с уравнениями более высоких порядков: Уравнение поперечных колебаний балки
где q(x) - масса балки на единицу длины; I(х) - момент инерции поперечного сечения балки; Уравнение изгиба пластинок
где q(x, у) - поверхностная нагрузка; D - цилиндрическая жесткость пластинки. Уравнение плоской задачи теории упругости (бигармоническое уравнение)
Определяемая дифференциальным уравнением математической физики функция ω должна удовлетворять заданным условиям на границе области интегрирования Ω и в начальный момент времени; эти условия называются граничными и начальными условиями; им должно удовлетворять решение уравнения. Наиболее часто встречаются следующие начальные и граничные условия: в начальный момент времени t=0 даны значения искомой функции ω(x, t) и ее производной по t:
на границе области Ω[x=x(s), y=y(s)] задана искомая функция ω(x, у):
или производная искомой функции по направлению нормали к границе:
При интегрировании линейных уравнений применяются следующие приемы. Meтод Фурье(метод разделения переменных) используется для решения линейных уравнений всех трех вышеуказанных типов. Изложим его, обратившись к задаче о свободных колебаниях закрепленной на концах струны. Полагая, что струна расположена на оси X, имеем для прогиба струны ω(x, t) (t - время) уравнение гиперболического типа:
Нужно найти решение этого уравнения, удовлетворяющее граничным условиям ω(0, t)=ω(l, t)=0 (х=0, х=l - концевые точки струны) и начальным условиям
где с - постоянная. Нетривиальное решение, удовлетворяющее граничным условиям, получается лишь при с=-k2(k≠0). Тогда
Отсюда
Из граничных условий следует A1=0, k=
удовлетворяющее при любых значениях констант аn, bn граничным условиям. Поскольку уравнение колебаний линейно и однородно, его решением будет также ряд
(при условии, что его можно два раза почленно дифференцировать). Коэффициенты аn, bnнаходятся из начальных условий. Из них следует, что
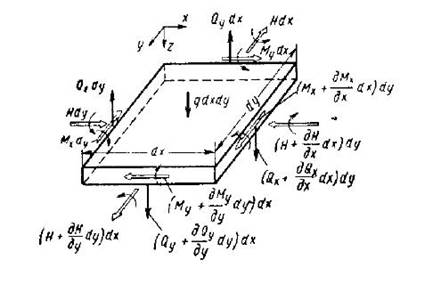
Отметим, что это получено решение для однородных граничных условий однородного уравнения о колебании струны. А начальные условия здесь были неоднородные. Однородность в данном случае означает равенство 0. В случае с неоднородными уравнениями и граничными условиями, как правило прибегают к так называемому методу вариации произвольных постоянных. Рассмотрим задачу о поперечном прогибе пластинки (рисунки 1-2). Схема равновесия ее элемента показана на рисунке 1.
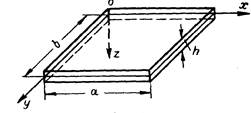
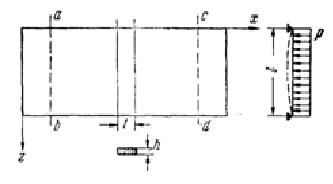
Рисунок 1. Схема равновесия элемента пластинки. Размеры пластин в направлении осей ох и оу обозначим буквами а и b соответственно, а толщину пластины - буквой h (рис.2).
Рисунок.2 Схема задачи. Дифференциальное уравнение изгиба абсолютно жестких пластин.
Уравнение (1) представляет дифференциальное уравнение в частных производных с постоянными коэффициентами. Здесь Пусть кромки х = 0 и х = а свободно оперты. Будем искать решение в виде (2).
Дифференциальное уравнение, определяющее функции fm (у).
Обыкновенное линейное дифференциальное уравнение четвертого порядка с постоянными коэффициентами. Общий интеграл дифференциального уравнения функции fm (у).
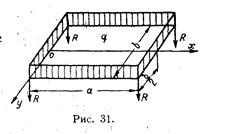
где Входящие в выражение постоянные интегрирования должны быть определены из условий закрепления опорных кромок пластины у=0 и у=b Изгиб пластины свободно опертой по всем четырем кромкам и загруженной равномерно распределенным давлением. Расчётная схема (рис.3).
Рис.3 Коэффициенты разложения нагрузки в ряд по синусам кратного аргумента.
При m=1,3,5…. Рассмотрим пластину постоянной толщины h, опертую на жесткий прямоугольный контур, у которого один в плане значительно больше другого (рис.4).
Рисунок 4. Схема задачи. Общий интеграл дифференциального уравнения, определяющего функцию fm (у) (10) Выражение для прогиба пластины, свободно опертой по всем четырем кромкам и загруженной равномерно распределенным давлением (13).
m=1,3,5... Постоянные Аm и Dm, должны быть определены из граничных условий для функций fm (у) при у =
Для производной fm (у) имеем : Сложим и вычтем эти два выражения друг из друга. Получим:
Запишем полное выражение для прогиба пластинки.
|
|
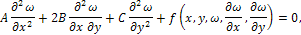
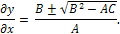
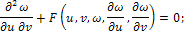
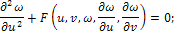
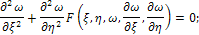
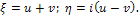
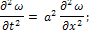
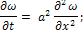
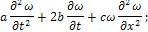
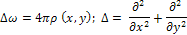
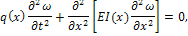
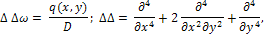
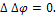
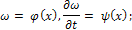
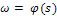
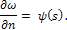
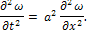
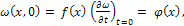 где f(x), φ(х) - заданные функции. Метод Фурье состоит в следующем. Ищется частное решение уравнения колебаний в виде ω=X(x)T(t). При подстановке этого выражения в указанное уравнение переменные разделяются, т. е. приходим к уравнению
где f(x), φ(х) - заданные функции. Метод Фурье состоит в следующем. Ищется частное решение уравнения колебаний в виде ω=X(x)T(t). При подстановке этого выражения в указанное уравнение переменные разделяются, т. е. приходим к уравнению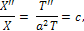
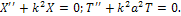

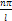 (n= 1, 2, ...). Таким образом, получается частное решение уравнения колебаний
(n= 1, 2, ...). Таким образом, получается частное решение уравнения колебаний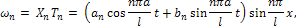
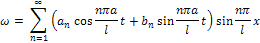
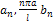 должны быть коэффициентами Фурье (см. 1.20.1) соответственно для функций f(x), φ(x) при их разложении в ряды по синусам, т. е.
должны быть коэффициентами Фурье (см. 1.20.1) соответственно для функций f(x), φ(x) при их разложении в ряды по синусам, т. е.
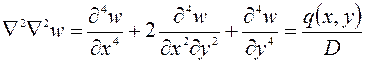 (1)
(1) - цилиндрическая жесткость пластин; q – нормальное давление на пластинку; Е – модуль Юнга; μ- коэффициент Пуассона; h – толщина пластинки.
- цилиндрическая жесткость пластин; q – нормальное давление на пластинку; Е – модуль Юнга; μ- коэффициент Пуассона; h – толщина пластинки.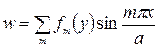 (2)
(2) (3)
(3) (4)
(4)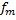 (у) - частное решение дифференциального уравнения (1).
(у) - частное решение дифференциального уравнения (1).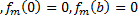 .
.
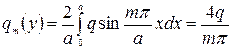 (10)
(10)
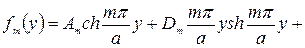
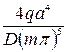 (13)
(13)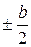 . По сравнению с выражением (10) здесь коэффициенты В и С приняты равными 0 на основании свойств симметрии искомого решения относительно оси у=0.
. По сравнению с выражением (10) здесь коэффициенты В и С приняты равными 0 на основании свойств симметрии искомого решения относительно оси у=0.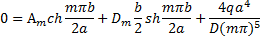

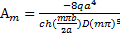 ;
; 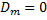 ;
;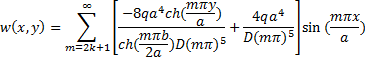
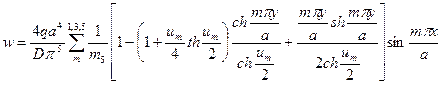 (13)
(13)