|
|
Тема4. Диференціальне числення функції однієї змінної.Практичне заняття 4.1 Тема.Знаходження похідних функції. Мета:Закріпити поняття похідної функції та її геометричного, механічного та економічного змісту. Добитися вміння автоматичного знаходження похідних основних елементарних функцій; відпрацювати навики знаходження похідних, застосовуючи основні правила диференціювання. Навчитися знаходити похідні складних функцій та функцій, заданих неявно і параметрично.
Завдання 1.Знайти похідні першого порядку. 1) у=2х 7) y=arcsinx+4 10) y=
Завдання 2.Знайти похідні складних функцій: 1) y=cos 3) y=cosx+lnx 4) y=lnsinx 5) y=e 7) y= 2 9) y=arcsin
Завдання 3.Знайти похідні другого порядку таких функцій: 1) y=e 3) y=cos 5) y= x*e
Завдання 4.Знайти похідні функцій, заданих параметрично: 1) 3) Завдання 5.Знайти похідні функцій, заданих неявно:
5) x siny-y cosx=0 6) e 7)
Практичне заняття 4.2. Тема: Диференціал функції. Застосування диференціала до наближених обчислень. Мета:Пояснити поняття диференціала функції. З’ясувати різницю між диференціалом та приростом функції в даній точці. Відпрацювати диференціали до наближених обчислень.
Завдання1. Знайти диференціали першого порядку функції. 1) 3) y=ln(sinx) 4) y= 5) y= 7) 9)
Завдання 2. Обчислити наближене значення функції у вказаних точках: 1)f(x)= 2)f(x)= 3)f(x)= 4)f(x)=x*ln(x-2) в точці х=3,012 5)f(x)=e
Завдання 3.Обчислити наближено: 1) 10 4) ln 7) (1.03)
Практичне заняття 4.3 Тема: Основні теореми диференціального числення. Правило Лопіталя. Мета:Вивчити основні теореми диференціального числення з метою подальшого їх застосування для дослідження функцій та побудови їх графіків. Навчитись розкривати невизначеності типу 0/0, ∞/∞, 0∙∞, ∞ - ∞, ∞0 , 00, застосовуючи правило Лопіталя.
Завдання 1. Використовуючи правило Лопіталя, знайти границі:
1) 3) 5) 7) 9)
Завдання 2. Використовуючи правило Лопіталя, розкрийте невизначеності: 1) 3) 5)
Практичне заняття 4.4. Тема: Дослідження функцій та побудова їх графіків.
Мета: Дати практику дослідження функції та побудови їх графіків. Систематизувати знання з теми «Диференціальне числення функцій однієї змінної». Навчитись застосовувати навички знаходження границь функцій, похідні функції, розкриття невизначеностей за правилом Лопіталя до дослідження функцій та побудови їх графіків. Завдання 1. Знайти інтервали зростання, спадання та екстремуми функції: 1) y= 3) y= x∙lnx 4)y= 5) y=15-x
Завдання 2. Знайти інтервали опуклості функції та точки перетину функції: 1) y= 3) y= 5) y=
Завдання 3. Знайти найбільше і найменше значення функції на вказаному відрізку. 1)y= 3)y=sinx+2x, [П;-П] 4)y= 5)y=
Завдання 4. Дослідити функції та побудувати їх графіки. 1) y=x 3) y= 5) y= 7) y= 9)
Тема 5. Диференціальне числення функції багатьох змінних. Практичне заняття 5.1.1 Тема: Функції багатьох змінних. Границя функції багатьох змінних. Мета:Засвоїти поняття функції багатьох змінних. Навчитися знаходити області визначення функції багатьох змінних, області неперервності, точки розриву. Дти практику обчислення границь функцій багатьох змінних.
Завдання1. Знайти значення функції у вказаних точках: 1) f(x.y.z)=x 2) f(x.y.z)= 3) f(x.y)=
Завдання 2. Знайти область визначення функції, заданих рівняннями: 1) z = 3) z = 5) z = 7) z = ln(4x 9) z =
Завдання 3. Обчислити границі функції багатьох змінних: 1) 3) 5) 7) 9)
Практичне заняття 5.1.2. Тема: Частинні похідні функції багатьох змінних. Похідні вищих порядків. Повний диференціал. Мета: Дати практику знаходження частинних похідних першого порядку та вищих порядків функції багатьох змінних, повного диференціалу. Засвоїти поняття градієнта функції багатьох змінних та його механічного змісту. Навчитися обчислювати наближено значення функції в точці, замінюючи її повний приріст повним диференціалом. Дати навички обчислення похідних складних функцій. Завдання1.Знайти частинні похідні першого порядку функцій двох змінних: 1) z=x 3) z=x 5) z= 7) z= 9) z=
Завдання 2.Знайти повні диференціали функцій двох змінних: 1) z=xy 3) z= 5) z= 7) z=y 9) z=
Завдання 3.Знайти градієнт grad Z та [grad Z] функції двох змінних в даній точці: 1) z=x 3) z=
Завдання 4. Обчислити наближено значення: 1)(1,08) 3)sin 1.59 * tg 3.09 4) 2.68
Практичне заняття 5.2 Тема: Екстремуми функцій двох змінних. Знаходження умовного екстремуму функції двох змінних методом Лагранжа. Мета: Засвоїти поняття екстремуму функцій багатьох змінних на прикладах функцій двох змінних. Закріпити навички знаходження частинних похідних першого та другого порядків функцій двох змінних та навчитися застосовувати їх до знаходження екстремумів функцій двох змінних, використовуючи необхідні умови існування екстремуму функцій багатьох змінних та достатні умови існування екстремуму функцій двох змінних. Засвоїти поняття умовного екстремуму функцій багатьох змінних. Навчитись знаходити умовний екстремум функцій двох змінних методом Лагранжа. Закріпити навички знаходження частинних похідних першого порядку та обчислення визначників третього порядку Завдання 1.Знайти екстремуми функції двох змінних: 1) z = x 3) z = 5) z = 2x 7) z = x 9) z = y
Завдання 2.Знайти екстремум функції Z=(x.y). за умови 1) z = xy за умови x 2) z = x 3) z = x 4) z = xy 5) z = x 6) z = xy за умови х+у=10 7) z = xy 8) z = 10x+y за умови 9) z = x 10) z = x
Практичне заняття 5.3 Тема:Визначення параметрів функціональної залежності методам найменших квадратів Мета: Навчатись визначати вид функціональної залежності змінних величин х та у в процесі, що досліджується. Дати практику застосування методу найменших квадратів для оцінки невідомих параметрів лінійної та параболічної функціональних залежностей. Література: Завдання 1. Величина товарообміну Х(тис.грн) та витрати обгу У(грн.) задані таблицею
Знайти аналітичну залежність між величинами Х та У.
Завдання 2.Величина товарообміну Х(ти. Грн.) та витрати обігу У(грн.) задані таблицею
Знайти аналітичну залежність між величинами Х та У.
Завдання 3.В таблиці вказано кількість внесених добрив на 1 га(Х) та врожай пшениці (У) у центнерах.
Обрати вигляд аналітичної залежності між величинами Х та У і визначити її параметри.
Завдання 4.Методом найменших квадратів визначити параметри лінійної функціональної залежності між величинами Х та У:
|
|
 2) у=
2) у=  3) у=4х
3) у=4х  4) y=
4) y=  5) y=log
5) y=log  6) y=2
6) y=2 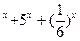
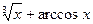 8) y=
8) y=  9) y=
9) y= 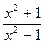
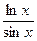
 2) y=
2) y= 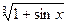
 6) y =
6) y = 
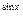 8) y=arcos(1-2x)
8) y=arcos(1-2x) 10) y=(tgx)
10) y=(tgx) 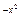 2) y=
2) y= 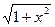
 4) y=
4) y= 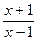
 6) y=x*sinx
6) y=x*sinx 2)
2) 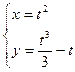
 4)
4) 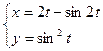
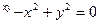
 8)
8) 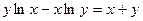
 2)
2) 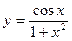
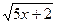
 6)
6) 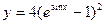
 8)
8) 
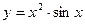 10)
10) 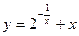
 в точці х=1,003
в точці х=1,003 в точці х=1,01
в точці х=1,01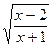 в точці х=3,032
в точці х=3,032 в точці х=3,97.
в точці х=3,97. 2) 1,025
2) 1,025 
 3)
3) 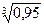
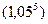 5) e
5) e  6) 10
6) 10 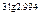
 8)
8)  9)
9) 

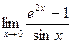
 4)
4) 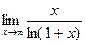
 6)
6) 
 8)
8) 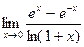
 10)
10) 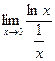
 2)
2) 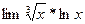
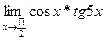 4)
4) 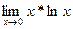
 6)
6) 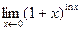
 2)y=x
2)y=x 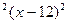
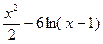
 6)y=e
6)y=e 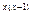
 2)y=
2)y= 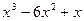
 4)y=
4)y= 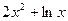
 6)
6) 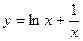
 2)y=
2)y=  [-3;7]
[-3;7] . [0;1]
. [0;1] .[-5;5] 6)y=x
.[-5;5] 6)y=x  . [-1;4]
. [-1;4]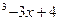 2) y=
2) y= 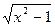
 4) y=
4) y= 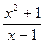
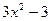 6) y=x*lnx
6) y=x*lnx 8) y=
8) y= 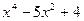
 10)
10) 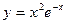
 в точках Мо(1,2,3), М(-2,1,-4)
в точках Мо(1,2,3), М(-2,1,-4) . (x.y.z)=(
. (x.y.z)=( 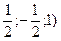
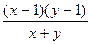 , Мо(1,-2), М(3,-2), М2(2,-2).
, Мо(1,-2), М(3,-2), М2(2,-2). 2) z =
2) z = 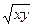
 4) z =
4) z = 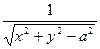
 6) z = ln(x+y)
6) z = ln(x+y) 8) z =
8) z = 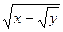
 10) z =
10) z = 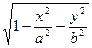
 2)
2) 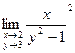
 4)
4) 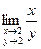
 6)
6) 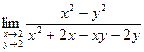
 8)
8) 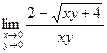
 10) lim
10) lim  .
. x
x 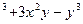
 4) z=
4) z= 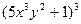
 6) z=
6) z= 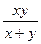
 8) z=ln(
8) z=ln( 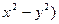
 10) z=
10) z= 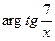
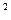 2) z=xy
2) z=xy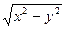 4) z=sinxy
4) z=sinxy  6) z=xy*cosxy
6) z=xy*cosxy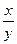
 10) z=ln(4-x
10) z=ln(4-x 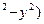
 , Мо(2,-1). 2) z=4-x
, Мо(2,-1). 2) z=4-x  , Мо(1,2)
, Мо(1,2) , Мо(0,3) 4) z=(x-y)
, Мо(0,3) 4) z=(x-y)  2)1,94
2)1,94 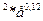
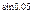 .
. 2) z = xy(1-x-y)
2) z = xy(1-x-y) 4) z = e
4) z = e 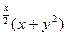
 6) z = 3
6) z = 3 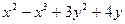
 8) z = x
8) z = x 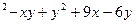
 10) z = y
10) z = y 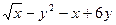
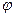 (x.y)=0:
(x.y)=0: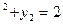
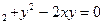
 за умови x+y=2, x
за умови x+y=2, x  .y=
.y= 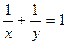
 за умови x
за умови x 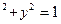
 за умови х+у=2, х
за умови х+у=2, х