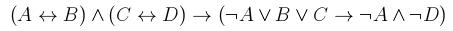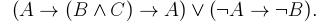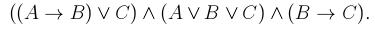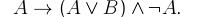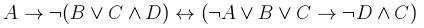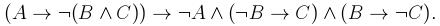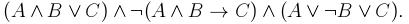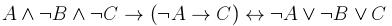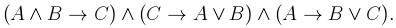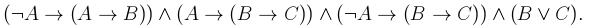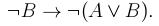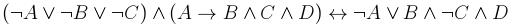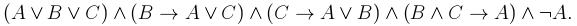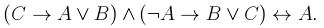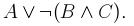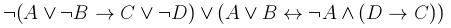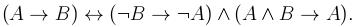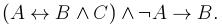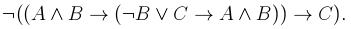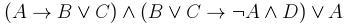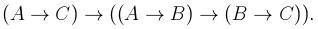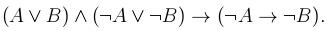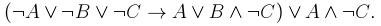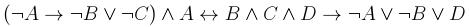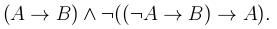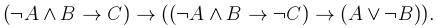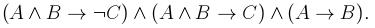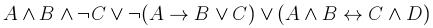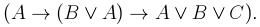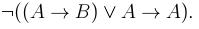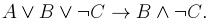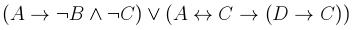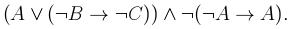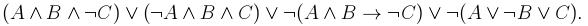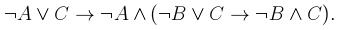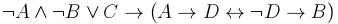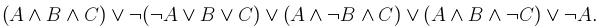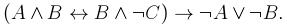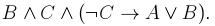Раздел 3. Логика высказываний

Вариант 1

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

2. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Если данное действительное число положительно или отрицательно, то его модуль положителен и это число не равно нулю. Данное число не равно нулю.

Следовательно, модуль этого числа положителен.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной

нормальным формам:

6. Найти формулу, задающую булеву функцию от двух переменных, которая принимает значение “И” тогда и только тогда, когда ее переменные принимают различные значения.

Вариант 2

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Я прихожу на лекции всегда без опоздания. Если я вечером пойду в кино, то поздно лягу спать. Если я поздно лягу спать, то опоздаю на лекции.

Следовательно, если я вечером в кино не пойду, то на лекции не опоздаю.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной

нормальным формам:

6. Найти формулу, задающую булеву функцию от двух переменных, которая принимает значение «И» тогда и только тогда, когда ее переменные принимают значение «Л».

Вариант 3

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Если данное число положительно или отрицательно, то оно действительное. Данное число не положительно и отлично от нуля.

Следовательно, это число действительное и отрицательное.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной

нормальным формам:

6. Найти формулу, задающую булеву функцию от двух переменных, которая принимает значение «И» тогда и только тогда, когда ее переменные принимают одинаковые значения.

Вариант 4

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Наша футбольная команда либо выигрывает матч, либо проигрывает его, либо сводит к ничьей. Команда матч не выиграла и не свела его к ничьей. Если матч выигран или проигран, то он не перенесен.

Следовательно, матч не перенесен и проигран.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной

нормальным формам:

6. Найти формулу, задающую булеву функцию от трех переменных, которая принимает значение «И» тогда и только тогда, когда большинство ее переменных принимают значение «И».

Вариант 5

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Если треугольник не равнобедренный, то он не правильный. Если треугольник прямоугольный, то он также не правильный. Данный треугольник правильный.

Следовательно, он равнобедренный или не прямоугольный.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной нормальным формам:

6. Найти формулу, задающую булеву функцию от трех переменных, которая принимает значение «И» тогда и только тогда, когда точно две ее переменные принимают значение «Л».

Вариант 6

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Множество A не пусто. Если множество A не пусто и A включается в B, то пересечение A и B не пусто. Либо A включается в B, либо множество A пусто.

Следовательно, пересечение A и B не пусто.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной нормальным формам:

6. Найти формулу, задающую булеву функцию от трех переменных, которая принимает значение «И» тогда и только тогда, когда лишь одна переменная принимает значение «Л».

Вариант 7

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Треугольник является либо остроугольным, либо прямоугольным, либо тупоугольным. Треугольник не остроугольный и не тупоугольный.

Следовательно, он прямоугольный.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной нормальным формам:

6. Найти формулу, задающую булеву функцию от трех переменных, которая принимает значение «И» тогда и только тогда, когда большинство ее переменных принимает значение «Л».

Вариант 8

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Если натуральное число простое, то оно не делится на числа, которые меньше его и больше единицы. Натуральное число не делится на числа, которые меньше его и больше единицы.

Следовательно, натуральное число простое.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной нормальным формам:

6. Найти формулу, задающую булеву функцию от двух переменных, которая принимает значение «И» тогда и только тогда, когда ее переменные принимают различные значения.

Вариант 9

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Данный треугольник либо равносторонний, либо прямоугольный. Если треугольник равносторонний, то он правильный. Данный треугольник не является прямоугольным.

Следовательно, он равносторонний и правильный.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной нормальным формам:

6. Найти формулу, задающую булеву функцию от трех переменных, которая принимает значение «Л» тогда и только тогда, когда все ее переменные принимают значение «И».

Вариант 10

1. Найти истинностное значение формулы

в интерпретации Φ: .

2. Определить, является ли данная формула выполнимой, тавтологией или противоречием:

3. Упростить данную формулу, используя законы логики:

4. С помощью понятия логического следования проверить правильность логического заключения в следующем рассуждении:

Если произведение двух чисел равно нулю, то одно из них равно нулю или оба равны нулю. Произведение двух чисел равно нулю, и одно из них не равно нулю.

Следовательно, другое число равно нулю.

5. Привести данную формулу к совершенным дизъюнктивной и конъюнктивной нормальным формам:

6. Найти формулу, задающую булеву функцию от трех переменных, которая принимает значение «И» тогда и только тогда, когда все ее переменные принимают значение «Л».