|
|
Рекурсивные процедуры и функции
Рекурсивным называется объект, который частично определяется через самого себя. Рекурсивные определения используются во многих областях науки и, особенно, в математике. Рассмотрим функцию определения факториала (n!); факториал – это произведение первых n натуральных чисел. Такое произведение можно вычислить с помощью программы, использующей оператор цикла for. Однако, существует другое определение факториала, в котором используется рекуррентные формулы: (1) 1!=1; (2) для любого n>0, n!=n*(n-1)! Определения, использующие рекуррентные формулы, называют рекурсивными определениями. Рекурсивные определения упрощают процесс вычислений. Например, в случае определения членов ряда Фибоначчи:
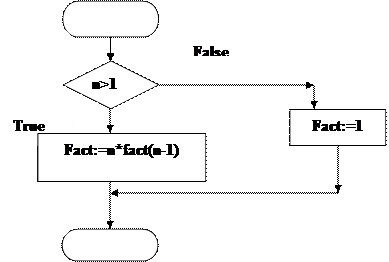
Рекурсивное определение значительно проще приведенной выше формулы и имеет следующий вид: (1) F(1)=1; (2) F(2)=1; (3) Для любого n>2, F(n)=F(n-1)+F(n-2). Рассмотрим рекурсивный алгоритм на примере накопления произведений. Пусть требуется написать программу, которая определяет произведение натуральных чисел от 1 до n: P=n!=1*2*…*n. Постановка задачи. Входные данные: n>0 – целое число. Выходные данные: P= n! – целое число. Аномалии. n<0, в программе не рассматриваются. Метод решения: для определения произведения использовать рекуррентные формулы: 1. 1!=1; 2. для любого n>0, n!=n*(n-1)! Блок-схема рекурсивной функции fact для определения факториала представлена на рис 9.10, а блок-схема основной программы – на рис. 9.11.
Текст программы на языке Паскаль.
Program Exam10; Var Ch, Proiz: integer; Function Fact(n: integer): integer; Var R: integer; Begin If n>0 then Fact:=n*Fact(n-1) Else Fact:=1; End; Begin Writeln('Input Ch>0 :'); Readln(Ch); If Ch>0 then begin Proiz := Fact(Ch); Writeln('Ch','!=',Proiz) end Else Writeln('Error! Ch<0'); Write('PRESS ANY KEY!!!'); Readln; End.
Результаты тестирования. 1. Исходные данные: Ch=3 Ch!=1*2*3=6 Результаты, выданные программой. Input Ch>0 : Ch!=6 PRESS ANY KEY!
2. Исходные данные: Ch=-3 Результат- сообщение «Error! Ch<0». Результаты, выданные программой. Input Ch>0 : -3 Error! Ch<0 PRESS ANY KEY!!! Рекурсивный процесс предполагает прямой ход или рекурсивный спуск и обратный ход или рекурсивный возврат. Прямой ход. При каждом рекурсивном обращении к функции создается новый экземпляр памяти всех локальных переменных и параметров этой функции, который запоминается в некоторой области памяти. Глубина рекурсии определяется количеством выполненных рекурсивных вызовов. Цепочка вызовов рекурсивных подпрограмм создает в памяти связанную последовательность областей памяти, организованных по принципу стека: доступной является область, размещенная последней. Прямой ход завершается тем вызовом подпрограммы, в котором истинно условие выполнения ее нерекурсивной части. Рекурсивный процесс выполнения функции Fact для Ch=3 имеет глубину рекурсии, равную 3, как показано в таблице ниже.
Обратный ход начинается с выполнения нерекурсивной части подпрограммы; после этого область стека, относящаяся к данному вызову удаляется и выполняется возврат к предыдущему вызову и т. д. Обратный ход завершается возвратом значения в программу, вызывавшую рекурсивную функцию. В рекурсивной процедуре или функции должно быть условие выполнения нерекурсивных операторов для обеспечения завершения рекурсии, иначе возможны бесконечные рекурсивные вызовы и аварийное завершение программы из-за переполнения доступной памяти для стека. В языке Паскаль допускается использование рекурсивных процедур. Рассмотрим пример рекурсивной процедуры на примере процедуры определения наибольшего общего делителя двух целых чисел. Задание. Определить наибольший общий делитель двух целых чисел. Постановка задачи. Входные данные: A , B – целые, положительные числа. Выходные данные: Nod – наибольший общий делитель A и B. Метод решения: рекурсивный алгоритм Евклида.
Алгоритм. Выдача наибольшего общего делителя двух целых чисел. Входные данные. СКАЛЯР A , B – целые, положительные числа. Выходные данные. СКАЛЯР Nod – целое число. Начало A:=0 B:=0 ЦИКЛ_ПОКА(A<=0 ИЛИ B<=0) Вывод(‘Input A,B : ’) ввод(A,B) КОНЕЦ_ЦИКЛА Findnod(A,B,Nod) Вывод(‘Nod(A,B)= ’,Nod) Конец
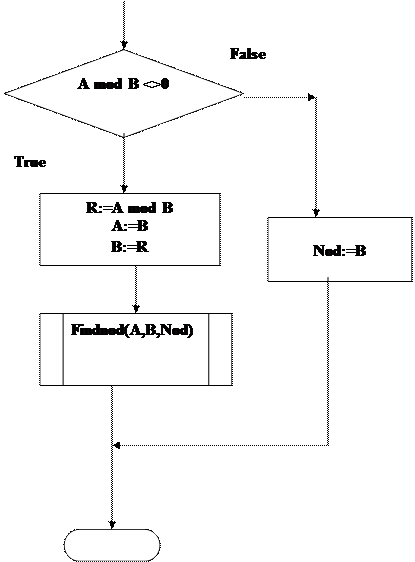
Алгоритм. Процедура определения наибольшего общего делителя двух целых чисел (findnod). Входные данные. СКАЛЯР A , B – целые, положительные числа. Выходные данные. СКАЛЯР Nod – целое число. Промежуточные данные. СКАЛЯР R – целое число. {остаток от деления } Начало ЕСЛИ (A mod B <>0) R:= A mod B A:=B B:= R Findnod(A,B,Nod) ИНАЧЕ Nod:=B КОНЕЦ_ЕСЛИ Конец Блок - схема программы
Program Exam7; Var A, B, Nod: integer; procedure findnod (A, B: integer; Var Nod: integer); Var R: integer; Begin If A mod B <>0 do Begin R:= A mod B; A:=B; B:=R; Findnod(A,B,Nod); End Else Nod:=B; End; Begin A:=0; B:=0; While (A<=0) or (B<=0) do begin Writeln('Input A,B <>0 :'); Readln(A,B); End; findnod(A,B,Nod); Writeln('Nod(A,B) = ',Nod); Readln; End.
Результаты тестирования. 1. Исходные данные: A=84 B=36 Результат: Nod(A,B)=12 d) Тестовый пример 2: A=84 B=56 Результат: Nod(A,B)=28 Результаты, выданные программой.
3. Тестовый пример1 Input A,B <>0 : Nod(A,B) = 12
4. Тестовый пример 2 Input A,B <>0 : Nod(A,B) = 28
Программа на языке Паскаль, использующая функцию. Program Exam11; Var A, B, Nod: integer; Function findnod (A, B: integer): integer; Var R: integer; Begin R:=1; While R<>0 do Begin R:=A mod B; A:=B; B:=R; End; findnod :=A; End; Begin A:=0; B:=0; While (A<=0) or (B<=0) do begin Writeln('Input A,B <>0 :'); Readln(A,B); End; Nod := findnod(A,B); Writeln('Nod(A,B) = ',Nod); Readln; End.
Результаты тестирования. 1. Тестовый пример 1 Исходные данные: A=84 B=36 Результат: Nod(A,B)=12 2. Тестовый пример 2 Исходные данные: A=84 B=56 Результат: Nod(A,B)=28 Результаты, выданные программой. Тестовый пример1 Input A,B <>0 : Nod(A,B) = 12
Тестовый пример 2 Input A,B <>0 : Nod(A,B) = 28
Модули
Одним из слабых мест механизма подпрограмм в Borland Pascal 7.0 является то, что они встроены в тело программы. Подпрограммы нельзя отдельно компилировать, отлаживать и использовать другими программами. Для того, чтобы можно было подпрограммы отдельно компилировать и вызывать многими программами, необходимо использовать модули. Модуль представляет собой совокупность различных компонент раздела описаний (констант, типов, переменных, подпрограмм), предназначенную для использования другими модулями и программами. Сам по себе модуль не является выполняемой программой (модуль нельзя запустить на выполнение). Однако он хранится и компилируется отдельно. Модуль имеет свой заголовок: Unit <имя модуля>; и два раздела: интерфейсную часть (interface) и исполняемую часть (implementation). Общая структура модуля имеет следующий вид: Unit <имя модуля>; Interface <объявления видимых объектов модуля: типов, констант, переменных, заголовков подпрограмм > implementation <описания скрытых объектов: процедур и функций> begin <операторы инициализации модуля[6]> end.
Интерфейсная часть может включать следующие компоненты: Interface Uses <список используемых модулей >; <раздел объявления констант (Const)> <раздел объявления типов (Type) > <раздел объявления переменных (Var)> <раздел заголовков процедур и функций>. Список используемых модулей содержит имена стандартных модулей, кроме модуля System, такие как Crt, Graph, Overlay, Dos, и имена модулей, созданных пользователем. Имена в списке разделяются запятыми. В разделе реализации (implementation) содержатся описания процедур и функций, заголовки которых объявлены в интерфейсной части. Кроме того, в исполнительной части могут быть объявлены типы, константы, переменные, которые используются в подпрограммах, но должны быть недоступны пользователю. В конце текста модуля всегда записывает ключевое слово “end” с точкой. Традиционные правила области действия глобальных и локальных переменных для модулей не выполняются. Языковая конструкция Unit (модуль) была специально включена в систему Borland Pascal для того, чтобы исключить влияние глобальных переменных, объявленных в главной программе, на описания подпрограмм, входящих в модули, которые эта программа использует. Поэтому, если все-таки возникает необходимость ввести доступные для всех модулей программы описания, то для этого надо создать модуль глобальных описаний, например:
Unit globals; Interface Const L=100; Type Tvector = array[1..L] of integer; Implementation End.
В этом случае исполнительная часть implementation является пустой. Рассмотрим пример модуля, содержащего процедуры и функции обработки одномерного массива, тип которого задан в модуле Globals. Этот модуль имеет имя Vector и включает следующие подпрограммы: o function Vect_Max(Vect:TVector; N:byte): byte; - возвращает индекс максимального элемента массива из N элементов; o function Vect_Min(Vect:TVector; N:byte): byte; - возвращает индекс минимального элемента массива; o procedure Print_Vect(Vect:TVector; N:byte); - выдает все элементы массива на экран; o procedure Vect_Inverse(Var Vect:TVector; i1,i2:byte); - меняет местами максимальный и минимальный элементы одномерного массива. Кроме того, модуль Vector использует модуль глобальных описаний globals. Текст модуля Vector. unit Vector; interface Uses globals; function Vect_Max(Vect:TVector; N:byte): byte; function Vect_Min(Vect:TVector; N:byte): byte; procedure Print_Vect(Vect:TVector; N:byte); procedure Vect_Inverse(Var Vect:TVector; i1,i2:byte); implementation function Vect_Max(Vect:TVector; N:byte): byte; Var Max:integer; im,i: integer; begin Max:=Vect[1]; im:=1; for i:=1 to N do if Max<Vect[i] then begin Max:=Vect[i]; im:=i; end; Vect_Max:=im; end; function Vect_Min(Vect:TVector; N:byte): byte; Var Min:integer; im,i: integer; begin Min:=Vect[1]; im:=1; for i:=1 to N do if Min>Vect[i] then begin Min:=Vect[i]; im:=i; end; Vect_Min:=im; end; procedure Print_Vect(Vect:TVector; N:byte); Var i: integer; begin writeln; for i:=1 to N do write(Vect[i],' '); end; procedure Vect_Inverse(Var Vect:TVector; i1,i2:byte); Var t: integer; begin t:=Vect[i1]; Vect[i1]:=Vect[i2]; Vect[i2]:=t; end; end. Процедуры и функции модуля Vector могут использовать любыми программами, которые храняться и компилируются в отдельных файлах. Пример программы Main, использующей этот модуль приведен ниже.
Program Main; Uses globals,vector; Var A: TVector; i,N:byte; n1,n2:byte; begin writeln; writeln(' Input N<=100'); readln(N); writeln(' Input array A of N elements :'); for i:=1 to N do read(A[i]); n1:=Vect_Max(A,N); n2:=Vect_Min(A,N); Vect_Inverse(A,n1,n2); Print_Vect(A,N); Readln; end.
Тестовый пример. Результаты, выданные программой Main.
Input N<=100 Input array A of N elements : 1 2 3 4 5 64 7 8 9 19
64 2 3 4 5 1 7 8 9 19
|
|