|
|
Задачи для контрольной работы №2МАТЕМАТИКА Направления подготовки Квалификация (степень) выпускника Бакалавр
Форма обучения Заочная Казань – 2015 ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ И ВАРИАНТЫ ЗАДАНИЙ ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
Указания по выполнению контрольных работ При выполнении контрольных работ студент должен руководствоваться следующим: · каждую работу следует выполнять в отдельной тетради, на внешней обложке которой должны быть указаны фамилия и инициалы студента, номер группы, полный шифр (номер зачетной книжки), номер контрольной работы и дата ее отсылки в институт; · решения всех задач и пояснения к ним должны быть достаточно подробными. Рекомендуется делать соответствующие ссылки на вопросы теории с указанием формул, теорем, выводов, которые используются при решении; все вычисления должны быть приведены полностью; чертежи и графики должны быть выполнены аккуратно, четко, с указанием единиц масштаба, координатных осей; обозначения к задачам должны соответствовать указаниям на чертеже. Для удобства рецензирования преподавателем контрольной работы следует оставлять на каждой странице широкие поля. После получения из института рецензированной работы студент должен исправить в ней все ошибки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и предоставить работу для повторного рецензирования, вместе с первоначально выполненной работой. Контрольная работа должна выполняться самостоятельно. В противном случае, работа не будет зачтена, даже если в ней все задачи решены верно. На зачете студент обязан предоставить зачтенную контрольную работу и по требованию преподавателя дать устные пояснения ко всем задачам, содержащимся в работе. Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра (номера зачетной книжки) (цифра 0 соответствует варианту 10). При этом если предпоследняя цифра учебного шифра есть число нечетное (т. е. 1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны во второй колонке таблицы 1. Если же предпоследняя цифра учебного шифра есть число четное или ноль (т. е. 0, 2, 4, 6, 8), то номера задач для соответствующего варианта даны в третьей колонке таблицы 1. Например, если шифр студента 4358, он должен решать задачи восьмого варианта из второй колонки таблицы 1; если же шифр студента 4328, он должен решать задачи восьмого варианта из третьей колонки табл. 1. Таблица 1
Задачи для контрольной работы №1 1—10. Даны координаты вершин треугольника ABC. Найти: 1) уравнение стороны АВ; 2) уравнение высоты CD, опущенной из вершины С на сторону АВ; 3) уравнение медианы АЕ;4) уравнение окружности, для которой медиана АЕ служит диаметром
11—20. Решить систему уравнений с тремя неизвестными двумя способами: 1) при помощи определителей по формулам Крамера, 2) с помощью обратной матрицы 11. 13. 15. 17. 19. 21—30. Решить систему уравнений методом Гаусса 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31—40. Вычислить
где
41―50. Даны координаты вершин пирамиды ABCD. Найти: 1) длину ребра AB; 2) угол между ребрами AB и AD; 3) угол между ребром AD и гранью ABC; 4) площадь грани ABC; 5) объем пирамиды; 6) уравнения прямой AB; 7) уравнение плоскости ABC; 8) уравнения высоты, опущенной из вершины D на грань ABC. Сделать чертеж
51―60. Вычислить определитель 51. 53. 55. 57. 59.
Задачи для контрольной работы №2 1—10. Для приведенной в табл. 2 выборки: а) построить вариационный и статистический ряды; б) построить полигоны частот и накопленных частот; в) вычислить среднее, моду, медиану, дисперсию, коэффициенты асимметрии и эксцесса. 11—20. Исходные данные — результаты выборочного обследования совокупности, где наблюдалась непрерывная случайная величина. Провести группировку выборки, разбив диапазон значений случайной величины на 5 интервалов. Для группированной выборки: а) построить полигон частот и гистограмму относительных частот; б) вычислить среднее, моду, медиану, дисперсию, коэффициенты асимметрии и эксцесса. Данные взять из табл. 3. 21—30. Найти 95% доверительный интервал для оценки математического ожидания 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31—40. Вычислить средние, дисперсии и коэффициент корреляции для выборки двух случайных величин X и Y. Построить диаграмму рассеивания. Данные взять из табл. 4. 41—50. Найти прямые регрессии Y на X и X на Y по данным выборки, приведенным в табл. 4. Построить диаграмму рассеивания и нанести на нее полученные прямые регрессии. Таблица 2
Таблица 3
Таблица 4
Основная литература: 1. Высшая математика для экономистов : учебник для вузов /под ред. Н.Ш. Кремера. – 3-е изд. –М. : ЮНИТИ-ДАНА, 2006. 2. Высшая математика для экономистов : учебник /под ред. Н.Ш. Кремера. – 3-е изд. –М. : ЮНИТИ-ДАНА, 2007. 3. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: учеб. пособие. – М. : КДУ, 2009. 4. Гмурман, В.Е.Теория вероятностей и математическая статистика: учеб. пособие. – М. : Высшее образование, 2006. 5. Гмурман, В.Е.Руководство к решению задач по теории вероятностей и математической статистике. – М. : Высшее образование, 2006. 6. Математика: учеб. пособие / Ю.М. Данилов, Л.Н. Журбенко, Г.А. Никонова, Н.В. Никонова, С.Н. Нуриева; под. ред. Л.Н. Журбенко, Г.А. Никоновой. – М. : ИФРА-М, 2009. 7. Журбенко Л.Н, Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дектярева О.М. Математика в примерах и задачах : учеб. пособие. – М. : ИНФРА-М, 2009. Дополнительная литература: 1. Шипачев, В.С. Основы высшей математики : учеб. пособие для вузов /под. ред. акад. А.Н.Тихонова – М. : Высшая школа, 2009. 2. Шипачев, В.С.Задачник по высшей математике : учеб. пособие для вузов. – М. : Высшая школа, 2009.
|
|



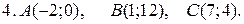

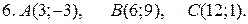

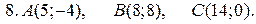
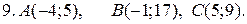
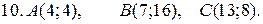
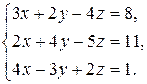 12.
12. 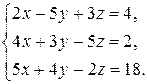
 14.
14.  16.
16. 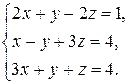
 18.
18. 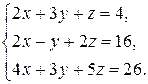
 20.
20. 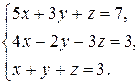
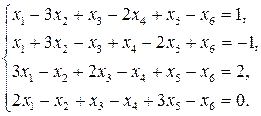
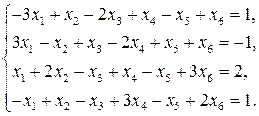
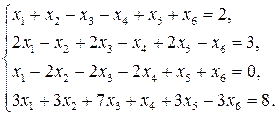
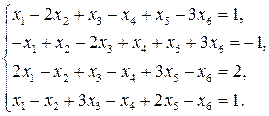
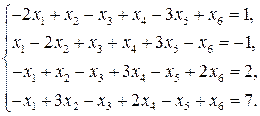

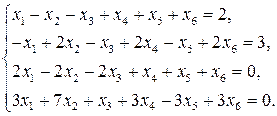
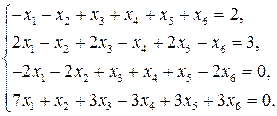

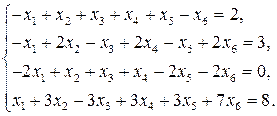
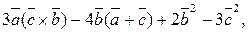
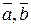 и
и  – векторы, координаты которых заданы в таблице:
– векторы, координаты которых заданы в таблице: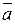
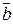






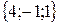




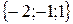


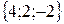

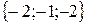



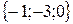









 52.
52. 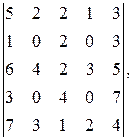
 54.
54. 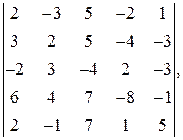
 56.
56. 
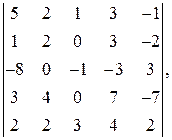 58.
58. 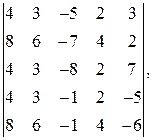
 60.
60. 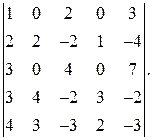
 нормально распределенной генеральной совокупности, зная выборочное среднее
нормально распределенной генеральной совокупности, зная выборочное среднее  , объем выборки
, объем выборки  и среднее квадратичное отклонение
и среднее квадратичное отклонение  .
.