|
|
Выбор инвестиционных проектов при лимитированном объеме финансовых ресурсовВсе предыдущие рассуждения неявно предполагали достаточность капитала для финансирования всех приемлемых инвестиционных проектов фирмы при неизменности его (капитала) стоимости. Если от этого допущения отказаться, то возникает проблема рационирования капитала. Всесторонний анализ этой проблемы выходит далеко за пределы базового курса финансового менеджмента и выливается в дискуссию о возможности возникновения ситуации, в которой у фирмы не хватает средств для того, чтобы профинансировать все инвестиции, имеющие положительные NPV, то есть увеличивающие акционерную стоимость. В рамках принятых моделей и с точки зрения рационального управления финансами фирмы такая ситуация не должна возникать в принципе, так как привлекательные инвестиционные проекты должны адекватно финансироваться, хотя бы в силу того, что эффективный финансовый рынок должен "откликаться" на возможность получить возврат на инвестиции, превышающий стоимость привлекаемых средств. Однако финансовые рынки далеко не всегда в достаточной степени информационно эффективны; помимо этого, объемы инвестиционных ресурсов могут лимитироваться на дивизиональном уровне управления предприятиями, и в некоторых других ситуациях. Наиболее простой вариант отбора проектов в условиях ограниченности инвестиционных ресурсов базируется на использовании критерия индекса доходности (см. выше). При этом предполагается, что стоимость капитала фирмы известна заранее и не зависит от принятия или непринятия тех или иных конкретных проектов, а сами проекты независимы. Отбор проектов тогда сводится к несложной процедуре, состоящей из двух этапов: 1. проекты с положительными NPV ранжируются по мере убывания их индексов доходности (PI); 2. проекты принимаются к реализации, начиная с первого в списке, пока суммарные начальные инвестиции в отобранные проекты не исчерпают установленный лимит капитальных вложений. Следует при этом отметить, что описанная процедура не претендует на выработку оптимальной инвестиционной стратегии.
Рассмотренные аспекты анализа инвестиционной привлекательности проектов отнюдь не исчерпывают всех проблем, возникающих в связи с инвестиционными проектами фирмы. Некоторые специфические аспекты проектно-инвестиционного анализа будут рассмотрены в приложениях к данной главе; другие рассматриваются в полных курсах финансового менеджмента, корпоративных финансов либо в специальных курсах.
Приложение 1. Применение методов расчета NPV и IRR для взаимоисключающих проектов Как уже отмечалось выше, использование методов расчета NPV и IRR для единичных проектов всегда ведет к одному и тому же результату с точки зрения выбора "принять – отвергнуть". Однако практика инвестиционного анализа достаточно часто сталкивается со случаями, когда проекты являются взаимоисключающими (или альтернативными)[40]. Примерами подобных ситуаций могут служить проект постройки гостиницы либо офисного комплекса на одном и том же участке земли, выбор между покупкой и лизингом объекта основных средств, размещение производственного предприятия возле основных источников сырья или рынка сбыта и т.п. Возникающая в таком случае проблема может быть проиллюстрирована следующим примером: Пример. Взаимоисключающие проекты А и В характеризуются следующими денежными потоками: Проект А: -50; 20; 20; 20; 20; 20 Проект В: -50; 5; 10; 20; 30; 60 При ставке дисконтирования 15% NPV проекта А составит 17.0; NPV проекта В составит 22.0. Внутренние нормы доходности проектов соответственно составят IRRA=28.65%;IRRB=26.72%. Таким образом, если руководствоваться методом расчета NPV, то предпочтительнее выглядит проект В, в то время, как руководствуясь критерием расчета IRR, можно прийти к выводу о предпочтительности проекта А. Противоположный порядок ранжирования проектов по степени их привлекательности объясняется неявным предположением о ставке реинвестирования денежных потоков, генерируемых проектами. Если при расчете NPV проектов средства реинвестируются под ставку дисконтирования, равную стоимости капитала (15% в нашем случае), то расчет внутренней нормы доходности IRR предусматривает реинвестирование под эту же ставку доходности (в нашем случае соответственно 28.65% и 26.72%). Легко заметить, что при стоимости капитала (или, что то же самое, средней доходности на один рубль вложенных средств) в 15% годовых у предприятия не возникнет проблем с реинвестированием средств под эту ставку9. Иное дело реинвестирование под более высокую ставку, равную IRR: весьма маловероятно, что проект потребует дополнительных инвестиций, совпадающих по величине и времени с поступлениями от реализации этого проекта. Более того, средневзвешенная стоимость капитала в 15% годовых делает привлечение дополнительных финансовых ресурсов под эту ставку заведомо более привлекательным, чем реинвестирование средств стоимостью в 28.65% или 26.72% годовых. Как следствие, именно критерий расчета чистой приведенной стоимости проекта дает однозначно верное ранжирование проектов. В рассмотренном конкретном примере противоречивые результаты применения методов расчета IRR и NPV обусловлены различием в интенсивности притоков денежных средств. Вычитая денежные потоки проекта А из денежных потоков проекта В мы получим приростные денежные потоки, формирующие проект, имеющий положительный NPV10. Выбор проекта А означал бы игнорирование проекта с положительным NPV, что было бы неверным с точки зрения основополагающей цели финансового менеджмента – максимизации стоимости фирмы.
Приведенные выше рассуждения могут быть проиллюстрированы следующим рисунком:
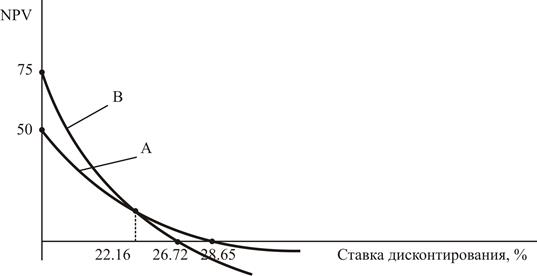
Рис.4.2. Зависимость NPV от ставки дисконтирования для двух взаимоисключающих проектов А и В.
Графики зависимости NPV проектов А и В от величины ставки дисконтирования пересекают горизонтальную ось в точках 28.65% и 26.72%, которые соответствуют значениям их внутренней нормы доходности. Пересечению этих кривых между собой соответствует точка 22.56%. Пересечение с вертикальной осью имеет место при нулевой ставке дисконтирования, что означает сумму недисконтированных денежных потоков от реализации проекта, уменьшенную на величину первоначальной инвестиции в проект. Как следует из рисунка, при значениях ставки дисконтирования, меньших 22.56% проект В более привлекателен, по сравнению с проектом А. Картина меняется на прямо противоположную, когда ставка дисконтирования становится выше 22.56%, причем при ставках, превышающих 26.72% приемлем только проект А. Если ставка дисконтирования выше 28.65%, оба рассматриваемых проекта будут неприемлемы (NPV<0). Помимо интенсивности притоков денежных средств, на степень привлекательности инвестиционного проекта может существенным образом повлиять масштаб инвестирования: на практике совершенно необязательно, чтобы взаимоисключающие проекты предусматривали одинаковый начальный объем инвестиций. Более того, вероятнее всего первоначальные вложения в такие проекты будут различаться, иногда весьма значительно. Если эти различия в масштабе инвестирования во внимание не принимать, то 100% дохода на 1 рубль будут выглядеть предпочтительнее 20% на 100 руб. (напомним, что проекты взаимоисключающие!) Как и выше, не составит труда показать, на основе дисконтирования приростных денежных потоков, что использование критерия расчета внутренней нормы доходности и в этом случае может привести к игнорированию дополнительного проекта с положительным NPV. Следовательно, метод расчета NPV и здесь предпочтителен: чистая приведенная стоимость тем выше, чем больше масштаб инвестирования. В заключение необходимо отметить, что метод расчета модифицированной внутренней нормы доходности (MIRR) свободен от описанного недостатка; однако расчет соответствующего показателя представляет собой достаточно громоздкую процедуру.
Приложение 2. Инвестиционные решения, связанные с заменой оборудования Практика использования метода расчета чистой приведенной стоимости проектов отнюдь не исчерпывается анализом рассмотренных выше ситуаций. Любое предприятие, занимающееся производственной либо торговой деятельностью рано или поздно сталкивается с необходимостью принятия решений, связанных с заменой оборудования. При этом в условиях крупных современных предприятий, характеризующихся несколькими уровнями управления, подобные решения часто делегируется с верхних уровней управления на более низкие, что требует формализации управленческих подходов. Последнее, в свою очередь, приводит к необходимости выработки политики в области замены оборудования. Финансовую природу соответствующих управленческих решений рассмотрим на следующем примере. Пример. Импортный станок стоимостью $16000, используемый при производстве медицинских инструментов имеет, по оценке его производителей, срок экономической жизни продолжительностью в 6 лет. По окончании этого периода вследствие износа деталей станок теряет требуемую точность, при этом капитальный ремонт не имеет экономического смысла. Ликвидационная стоимость станка после 6 лет эксплуатации равна нулю. В силу высокотехнологичного характера производства и высокой конкуренции на рынке медицинских инструментов, денежные потоки даже в течение срока экономически обоснованной эксплуатации станка неравномерны (моральное старение оборудования снижает привлекательность изготавливаемой продукции в глазах потребителей). Перед фирмой встает следующая проблема: эксплуатировать станок в течение всего срока его экономической жизни, или продать его до истечения нормативных 6 лет, заменив на более современную версию. Чистые денежные потоки от реализации проекта (по годам) и динамика изменения рыночной стоимости представлены в таблице 4.2. Таблица 4.2. Чистые денежные потоки от эксплуатации станка и его рыночная стоимость
* Для простоты рассуждений будем предполагать, что рыночная стоимость станка на конец соответствующего года дана с учетом налоговых последствий от реализации; иначе возникла бы необходимость ввести в расчет годовую норму амортизации и ставку налога на прибыль. Предполагается также, что решение об обновлении оборудования осуществляются по окончании соответствующего года.
Если приемлемая ставка дисконтирования составляет 20%, то легко рассчитать NPV проектов, предусматривающих замену станка соответственно после одного, двух, трех, четырех, пяти и шести лет эксплуатации (все расчеты ведутся в тыс. долл.): NPV1 = -16 + (8+14)/1.2 = 2.333 NPV2 = -16 + 8/1.2 + (7.5+12)/1.22 = 4.208 NPV3 = -16 + 8/1.2 + 7.5/1.22 + (7+10)/1.23 = 5.713 NPV4 = -16 + 8/1.2 + 7.5/1.22 + 7/1.23 + (6.5+6)/1.24 = 5.954 NPV5 = -16 + 8/1.2 + 7.5/1.22 + 7/1.23 + 6.5/1.24 + (6+2)/1.25 = 6.276 NPV6 = -16 + 8/1.2 + 7.5/1.22 + 7/1.23 + 6.5/1.24 + 6/1.25 + 5.5/1.26 = 7.314 Максимальная чистая приведенная стоимость эксплуатации станка в течение всего срока его экономической жизни не означает, однако, что именно этот вариант окажется в конечном счете оптимальным. В данном случае мы имеем дело с проектами различной продолжительности. Однако, в отличие от рассмотренных выше, эти проекты однозначно являются повторяющимся. Как следствие, каждый из проектов потребуется повторить столько раз, сколько это необходимо для достижения равного числа денежных потоков. Наименьшее общее кратное чисел 1, 2, 3, 4, 5 и 6 равно 60. Соответственно, решение задачи "вручную" методом цепного повтора потребует достаточно громоздких вычислений. Упростить вычислительную часть задачи позволяет метод эквивалентного аннуитета. Суть метода заключается в вычислении эквивалентного аннуитетного платежа, то есть платежа, при котором NPV рассматриваемого проекта, осуществленного один раз совпадает с дисконтированной стоимостью аннуитета той же срочности с равными между собой платежами. Сравнивая затем рассчитанные значения платежей между собой для каждого из вариантов, выбирают наибольшее, как соответствующее наибольшему NPV при повторе каждого из проектов бесконечно число раз11. В нашем случае удобно воспользоваться формулой дисконтированной стоимости срочного аннуитета с равными между собой платежами (2.7): NPV1 = 2.333 = А1/(1+0.20), откуда А1 ≈ 2.80; NPV2 = 4.208 = А2[1-1/(1+0.2)2]:0.20, откуда А2 ≈ 2.75; NPV3 = 5.713 = А3[1-1/(1+0.2)3]:0.20, откуда А3 ≈ 2.71; NPV4 = 5.954 = А4[1-1/(1+0.2)4]:0.20, откуда А4 ≈ 2.30; NPV5 = 6.276 = А5[1-1/(1+0.2)5]:0.20, откуда А5 ≈ 2.10; NPV6 = 7.314 = А6[1-1/(1+0.2)6]:0.20, откуда А6 ≈ 2.20. Из сравнения полученных значений Аi следует парадоксальный на первый взгляд вывод: при заданных темпах падения рыночной стоимости станка и денежных потоков от его эксплуатации разумнее всего по истечении каждого года производить его замену.
Приложение 3. Анализ и учет риска в инвестиционном проектировании Следует сразу оговориться, что речь в данном разделе пойдет о применении методов риск-анализа непосредственно к денежным потокам проекта. Это означает, в частности, что мы отказываемся от сделанного выше допущения о том, что принятие инвестиционного проекта не изменяет уровня риска компании в целом. Напомним, что подобное допущение позволяло использовать единую ставку дисконтирования для всех проектов фирмы и не беспокоиться по поводу точности оценки денежных потоков от реализации проекта. Одним из наиболее очевидных способов ослабить некоторую ограниченность, свойственную анализу инвестиционных проектов, являются имитационное моделирование и анализ. Рамки базового курса финансового менеджмента не позволяют углубиться в технику этой достаточно специфической области финансового моделирования, однако полезно сформулировать основные направления соответствующего анализа. Использование единой ставки дисконтирования для всех инвестиционных проектов организации основывается на неявном предположении о том, что все факторы, участвующие в формировании чистых денежных потоков от реализации проекта характеризуются одной и той же степенью риска. При этом в рамках используемой модели риск-анализа ожидаемый доход представляется в форме суммы произведений возможных исходов на соответствующие вероятности. Учитывая, что сам процесс отбора возможных исходов инвестиционной операции и присвоение им соответствующих вероятностей неизменно носит отпечаток субъективности, можно предложить осуществлять этот процесс применительно не к самим чистым денежным потокам от реализации проекта, а к их составляющим: прогнозной доле рынка и темпам ее прироста, продажным ценам и стоимости ресурсов и др. Ведь отнюдь не факт, что все эти и другие факторы будут иметь одинаковую степень неопределенности. Более того, при анализе альтернативных проектов также может быть принята во внимание различная степень неопределенности составляющих денежных потоков от их реализации. Результатом соответствующего анализа должна стать уточненная оценка риска величины NPV для единичного или альтернативных проектов. Соответственно, решение о выборе проекта будет выглядеть более обоснованным.
Анализ чувствительности Естественным продолжением изложенного выше подхода, предусматривающего учет различной степени неопределенности отдельных факторов, участвующих в формировании прогнозных денежных потоков от реализации проекта, является анализ чувствительности результатного показателя - NPV или IRR - к изменению одного из этих факторов. Анализ начинают с расчета базового варианта – значения NPV или IRR, соответствующего наилучшим оценкам, доступным на момент составления прогноза. Затем, задаваясь процентными отклонениями от величин факторов, в отношении которых возможны ошибки прогнозирования, рассчитывают возможные отклонения результатного показателя от базового (ожидаемого) варианта (при этом, варьируя один параметр, остальные оставляют фиксированными). В качестве иллюстрации рассмотрим следующий пример: Организация общественного питания планирует обогатить предлагаемое меню набором кошерных блюд. Срок экономической жизни проекта оценивается в 3 года, необходимые инвестиции в основной и оборотный капитал составят 60 тыс. руб. В день планируется продавать 40 кошерных обедов в среднем по 80 руб. Стоимость продуктов оценивается в 55 руб. на один обед, дополнительные фиксированные затраты (без амортизации) - в 6000 руб. в месяц. Прогнозируемое расширение ассортимента повлечет, по расчетам организации, снижение спроса на обычные блюда, что приведет к падению чистого денежного потока от их реализации на 18 тыс. руб. в месяц. Ожидаемый чистый денежный поток от реализации проекта составит (из расчета 30 дней в месяце) CFмес = (80-55)•40•30 – 6000 – 18000 = 6000 руб. в месяц. Годовой чистый прирост денежных средств CFi составит, соответственно 72000 руб. Если принять стоимость капитала организации равной 40%, то ожидаемая чистая приведенная стоимость проекта составит (в тыс. руб.) NPV = - 60 + 72/1.4 + 72/1.42 + 72/1.43 = - 60 + 114.402 = 54.402 тыс. руб. Предположим теперь, что из всех факторов, участвовавших в расчете чистых денежных потоков, наименее предсказуемыми являются данные об объемах продаж (в натуральных единицах), о стоимости продуктов и об издержках упущенных возможностей. Анализ чувствительности NPV проекта к изменению перечисленных выше факторов удобно представить в форме таблицы, где показано базовое значение NPV и возможные отклонения в результате погрешности прогнозирования отдельных факторов:
Таблица 4.3. Анализ чувствительности NPV проекта
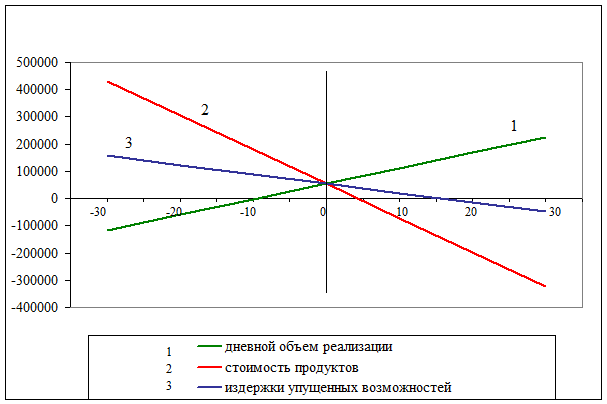
Полученные результаты можно проиллюстрировать графиком зависимости NPV от погрешности в прогнозировании, представленном на рис. 4.3. Очевидно, что наиболее сильная зависимость значения NPV наблюдается от стоимости продуктов, используемых при приготовлении одного обеда. Наименьший эффект имеют изменения величины возможных потерь от падения реализации "некошерной" продукции.
Рис. 4.3. Зависимость NPV от величины погрешности прогнозирования
Проведенный анализ может послужить основанием для достаточно важных выводов: если по поводу возможного эффекта каннибализации можно особенно не волноваться, то изменение себестоимости обеда может кардинальным образом изменить экономическую эффективность проекта. Как следствие, необходимо особенно внимательно отнестись к прогнозированию цен на закупаемые продукты и предпринять меры к возможному их снижению.
Дерево решений Неопределенность и обилие альтернатив, сопутствующих реализации инвестиционных проектов наводят на мысль о необходимости привлечения инструментов структуризации процесса принятия инвестиционного решения. Одним из таких инструментов служит так называемое дерево решений, представляющее собой графическое изображение возможных решений и их последствий. В системе координат Денежные потоки от реализации проекта – Время дерево вероятностей выглядит следующим образом:
Денежные потоки
Период
Рис. 4.4. Дерево решений
Точки, соответствующие моменту времени, когда возникает необходимость принятия управленческого решения, носят название узлов выбора и обозначаются квадратиком; ветви, исходящие из узла выбора представляют собой альтернативные решения. Точки, после которых развитие событий может пойти по нескольким направлениям, называют узлами события и обозначают кружочком. Ветви, исходящие из таких точек представляют собой альтернативные возможности развития событий. Соответствующие (присвоенные) каждому варианту развития событий вероятности обычно записываются в скобках возле каждой ветви; перемножая эти вероятности на чистые денежные потоки от реализации каждого варианта, получают ожидаемую денежную стоимость (EMV – Expected Monetary Value) для каждого узла событий. В качестве EMV может выступать, в частности, значение NPV. Анализ рассчитанных значений EMV позволяет сделать обоснованный выбор направления инвестирования. В заключение можно привести некоторые общие принципы построения дерева решений [Ли, Финнерти]: 1. Для отображения на графике нужно включать только важные, "узловые" решения или события, чтобы "дерево не превратилось в куст"; 2. Метод предполагает субъективную оценку вероятности тех или иных событий; 3. Дерево решений нужно строить в хронологическом порядке, чтобы совпадали логика развития событий и логика решений.
|
|