Обратная связь
|
РОЗВ’ЯЗАННЯ ПОКАЗНИКОВИХ І ЛОГАРИФМІЧНИХ РІВНЯНЬ
Вправи
1. Розв'язати показникові рівняння:
-
 = 2; = 2; -
 = 49; = 49;
-
 = = 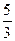 ; ; - 25
 = 1; = 1; - 3
 = 3; = 3; - 0,2
 = 0, 008; = 0, 008; - 0,2
 = 125; = 125; -
 = 8; = 8; - 2
 = =  ; ; - 5
 = =  ; ; - 9
 = 3; = 3; -
 = 4; = 4; -
 = 27; = 27; -
 = 3; = 3; -
 = 1; = 1; - 81
 = 3; = 3; - 2
 = 4; = 4; -
 = =  ; ; -
 = = 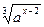 ; ; - 15
 = 1; = 1; - 2
 = -2; = -2; - 5
 = 125; = 125; -
 = =  ; ; -
 = =  ; ; - 5
 = 5 = 5  ; ; - 7
 = 7 = 7  ; ; - 2
 = 4; = 4; - 0,5
 = 0,125; = 0,125; -
 = =  ; ; - 2
 - 2 = 0; - 2 = 0; - 3
 -1 = 0; -1 = 0; - 3
  3 = 81; 3 = 81; - 2
 2 2  = 32; = 32; - 3
 = 9. = 9.
*2. Розв'язати показникові рівняння:
1. 3х · 52х-3 = 45;
2. 2х · 3х+1 = 108;
3.  = =  ; ;
4.  = =  ; ;
5.  = =  ; ;
-
 = =  ; ;
7. 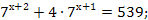
8. 
9. 
10. 
11. 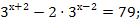
12. 5 · 9  + 9 + 9  = 406; = 406;
13. 5 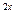 + 4 · 5 + 4 · 5  - 5 = 0; - 5 = 0;
14. 6 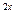 + 5 · 6 + 5 · 6  - 6 = 0; - 6 = 0;
15. 3 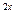 - 2 · 3 - 2 · 3  = 3; = 3;
16.  - -  = 3; = 3;
17.  - -  = 2; = 2;
18. 49  - 6 · 7 - 6 · 7  - 7 = 0; - 7 = 0;
19. 64  - 7 · 8 - 7 · 8  - 8 = 0; - 8 = 0;
-
 + +  = 5; = 5; -
 + +  = 10; = 10; -
 + +  = 80; = 80; -
 = = 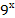 ; ; -
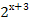 - -  = =  - -  -
 + +  = =  + +  ; ; -
 = 0; = 0; -
 = =  ; ; -
 = 0; = 0; -
 = 0; = 0; -
 = 0. = 0.
Тема. Розв’язання показникових нерівностей
План
1. Графік показникової функції.
2. Схема рівносильних перетворень найпростіших показових нерівностей.
1. Графік показникової функції у =  , де , де  і і  . .
| 
| 
|  зростає
зростає
|  спадає
спадає
| | 2. Схема рівносильних перетворень найпростіших показових нерівностей
| 
| 
|  > >   f(x) > g(x)
знак нерівності зберігається f(x) > g(x)
знак нерівності зберігається
|  > >   f(x) < g(x)
знак нерівності змінюється на протилежний f(x) < g(x)
знак нерівності змінюється на протилежний
| | Приклади
| 
 Функція у =
Функція у = 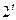 є зростаюча, отже:
х – 3 > 2,
х > 5.
Відповідь: (5; + є зростаюча, отже:
х – 3 > 2,
х > 5.
Відповідь: (5; +  ). ).
| 
 Функція в =
Функція в =  є спадною, отже: є спадною, отже:

 .
Відповідь: (- .
Відповідь: (-  ; 5) ; 5)
| | 3. Розв’язання більш складних показникових нерівностей
| | Орієнтир
| Приклад
| | За допомогою рівносильних перетворень ( за схемою розв’язання показникових рівнянь) дану нерівність приводять до нерівності відомого виду (квадратному, дробовому і т.д.). Після розв’язання отриманої нерівності приходимо до найпростіших показникових нерівностей
| 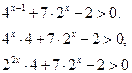
 Заміна Заміна  дає нерівність дає нерівність 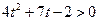 , розв’язання якого , розв’язання якого  або або  Обернена заміна дає
Обернена заміна дає  (розв’язаннь немає) або (розв’язаннь немає) або 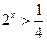 , звідки , звідки  Відповідь: (-2; +
Відповідь: (-2; +  ). ).
|
Вправи
1. Розв'язати нерівність
1) 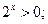
2) 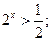
3) 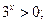
4)  ; ;
5)  ; ;
6)  ; ;
7) 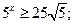
8)  ; ;
9)*  . .
Тема. Поняття логарифма числа. Властивості логарифмів
План
1. Логарифм числа.
2. Основна логарифмічна тотожність.
3. Властивості логарифмів.
| 1. Логарифм числа
| | Визначення
| Приклади
| Логарифмом додатного числа b за основою a
(a > 0,  ) називається показник степеня, в який потрібно піднести a, щоб одержати число b.
Позначення: loga b ) називається показник степеня, в який потрібно піднести a, щоб одержати число b.
Позначення: loga b
| 1) log4 16 = 2, оскільки 42 = 16;
2) log7  = =  , тому що , тому що  = =  ;
3) lg 1000 = 3, оскільки 103 = 1000 ;
3) lg 1000 = 3, оскільки 103 = 1000
| | Десятковий логарифм – це логарифм за основою 10.
Позначення: log10 b = lg b
| Натуральний логарифм – це логарифм за основою е (е – ірраціональне число, наближене значення якого: е  2,7).
Позначення: logе b = ln b 2,7).
Позначення: logе b = ln b
| 4) ln  = - 2, тому що е-2 = = - 2, тому що е-2 = 
| | 2. Основна логарифмічна тотожність
|  a > 0,
a > 0,  , b > 0 , b > 0
| 1)  ;
2) ;
2)  . .
| - Властивості логарифмів і формули логарифмування
(a > 0,  , х > 0, в > 0) , х > 0, в > 0)
| 1) 
| Логарифм одиниці за будь-якою основою дорівнює нулю
| 2) 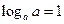
| Логарифм числа a за основою a дорівнює одиниці
| 3) 
| Логарифм добутку додатних чисел дорівнює сумі логарифмів множників.
| 4) 
| Логарифм частки додатних чисел дорівнює різниці логарифмів діленого й дільника
| 5) 
| Логарифм степеня додатного числа дорівнює добутку показника степеня на логарифм основи
| | 4. Формула перехід до логарифмів з іншою підставою
|  (a > 0,
(a > 0,  , х > 0, b > 0, , х > 0, b > 0, 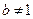 ) )
| | Наслідки
| 
| 
|
Вправи
1.Перевірте, чи вірна рівність:
1)  = 4; = 4;
2)  = 3; = 3;
3)  ; ;
4)  ; ;
5)  ; ;
6)  = 3. = 3.
2.Обчислити:
1)  ; ;
2) 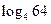 ; ;
3)  ; ;
4)  ; ;
5)  ; ;
6)  . .
3. Користуючись основною логарифмічною тотожністю, спростити вираз:
1) 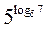 ; ;
2) 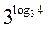 ; ;
3)  ; ;
4)  ; ;
5)  . .
4. Прологарифмуйте даний вираз за даною основою, якщо : :
1) 10a3c4 за основою 10;
2)  за основою 10; за основою 10;
3)  за основою е; за основою е;
4)  за основою 3. за основою 3.
5. Відомо, що  , ,  . Виразити через a і b: . Виразити через a і b:
1) 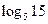 ; ;
2)  ; ;
3)  ; ;
4)  . .
6. Знайдіть х, якщо:
1)  ; ;
2)  ; ;
3)  ; ;
4)  . .
Тема. Логарифмічна функція, її властивості й графік
План
1. Логарифмічна функція.
2. Графік логарифмічної функції.
3. Властивості логарифмічної функції.
| 1. Поняття логарифмічної функції
| Логарифмічною функцією називається функція виду у = loga x,  . .
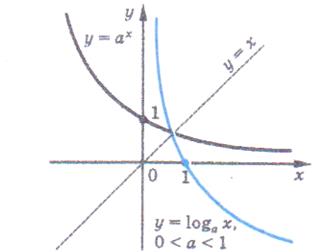
| | 2. Графік логарифмічної функції
| Функції у =  і у = loga x ( і у = loga x (  ) – взаємно обернені функції, тому їх графіки симетричні відносно прямою у = х. ) – взаємно обернені функції, тому їх графіки симетричні відносно прямою у = х.
| 
| 
| 
| 
| | 3. Властивості логарифмічної функції
| 1) Область визначення: D(у) = (0; +  ) )
| 2) Область значень: Е(у) = (-  ; + ; +  ) )
| | 3) Функція ні парна, ні непарна
|
| | 4) Точки перетину з осями координат:
с віссю Оу – немає з віссю Ох: х = 1, у = 0
| | 5) Проміжки зростання та спадання:
| функція в = loga x при  зростає на всій області визначення
зростає на всій області визначення
| функція в = loga x при  спадає на всій області визначення
спадає на всій області визначення
| | 6) Проміжки знакосталості
| 
| 
| | в = loga x > 0 при x > 1,
в = loga x < 0 при 0 < x < 1
| в = loga x > 0 при 0 < x < 1,
в = loga x < 0 при x > 1
| | 7) Найбільшого та найменшого значень функціїї не має
| 8) loga a = 1
loga (uv) = loga u + loga v (u > 0, v > 0)
loga  = loga u - loga v (u > 0, v > 0)
loga un = n loga u = loga u - loga v (u > 0, v > 0)
loga un = n loga u
 = =  
|
Вправи
1. Знайдіть область визначення функції:
1) у = log11 (2х + 6);
2) у =  ; ;
3) у =  ; ;
4) у =  ; ;
5) у =  . .
2. Зобразити схематично графік функції:
1) у =  ; ;
2) у =  ; ;
3) у = 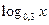 ; ;
4) у =  ; ;
5) у =  ; ;
6) у =  ; ;
7) у =  ; ;
8) у =  ; ;
9) у = 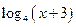 ; ;
10) у =  ; ;
11) у =  . .
3. Порівняйте числа:
1)  і і  ; ;
2) 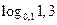 і і  ; ;
3)  і і  ; ;
4)  і і  ; ;
5)  і 0; і 0;
6)  і 1. і 1.
Тема. Розв’язання логарифмічних рівнянь
План
1. Розв’язання найпростіших логарифмічних рівнянь.
2. Використання рівнянь - наслідків.
3. Рівносильні перетворення логарифмічних рівнянь.
| 1. Розв’язання найпростіших логарифмічних рівнянь
| | Орієнтир
| Приклад
| Якщо а – число (  ), то ), то
 (використовуємо визначення логарифма)
(використовуємо визначення логарифма)
|  х – 1 = 32,
х = 9 + 1,
х = 10.
Відповідь: 10
х – 1 = 32,
х = 9 + 1,
х = 10.
Відповідь: 10
| | 2. Використання рівнянь - наслідків
| | Орієнтир
| Приклад
| | Якщо із припущення, що перша рівність вірна, випливає, що кожне наступне вірно, те гарантуємо, що одержуємо рівняння-наслідок. При використанні рівнянь – наслідків не відбувається втрати коренів вихідного рівняння, але можлива поява стороннього кореня. Тому перевірка отриманого кореня підстановкою у початкове рівняння є складовою частиною розв’язання.
| 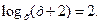 За визначенням логарифма одержуємо
х + 2 = х2,
х2 – х – 2 = 0,
х1 = -1, х2 = 2.
Перевірка: х = -1 – сторонній корінь (в основі логарифма одержуємо від’ємне число); х = 2 – корінь, тому що
За визначенням логарифма одержуємо
х + 2 = х2,
х2 – х – 2 = 0,
х1 = -1, х2 = 2.
Перевірка: х = -1 – сторонній корінь (в основі логарифма одержуємо від’ємне число); х = 2 – корінь, тому що
 Відповідь: 2
Відповідь: 2
| | 3. Рівносильні перетворення логарифмічних рівнянь
| | Заміна змінних
| | Орієнтир
| Приклад
| | Якщо в рівняння (нерівність або тотожність) змінна входить у тому самому виді, то зручно відповідний вираз зі змінною позначити однієї буквою (новою змінною).
|  .
Заміна: .
Заміна:  , ,
 , ,
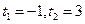 .
Отже, .
Отже, 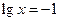 або або  .
Тоді х = 10-1 = 0,1 або х = 103 = 1000.
Відповідь: 0,1; 1000. .
Тоді х = 10-1 = 0,1 або х = 103 = 1000.
Відповідь: 0,1; 1000.
| Рівняння виду  ( (  ) )
| | Орієнтир
| Приклад
|  (враховуємо ОДЗ і дорівнюємо вирази, які стоять під знаками логарифмів)
(враховуємо ОДЗ і дорівнюємо вирази, які стоять під знаками логарифмів)
|  ОДЗ:
ОДЗ: 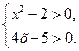 На цій ОДЗ дане рівняння рівносильне рівнянням: х2 – 2 = 4х – 5,
х2 – 4х + 3 = 0,
х1 = 1, х2 = 3,
х1 = 1 – сторонній корінь (не задовольняє умовам ОДЗ);
х2 = 3 – корінь (задовольняє умовам ОДЗ).
Відповідь: 3
На цій ОДЗ дане рівняння рівносильне рівнянням: х2 – 2 = 4х – 5,
х2 – 4х + 3 = 0,
х1 = 1, х2 = 3,
х1 = 1 – сторонній корінь (не задовольняє умовам ОДЗ);
х2 = 3 – корінь (задовольняє умовам ОДЗ).
Відповідь: 3
| | Рівносильні перетворення рівнянь в інших випадках
| | Орієнтир
| Приклад
| | 1. Ураховуємо ОДЗ даного рівняння ( і уникаємо перетворень, що приводять до звуження ОДЗ);
2. Стежимо за тим, щоб на ОДЗ кожне перетворення можна було виконати як у прямому, так і у зворотному напрямках зі збереженням вірної рівності
|  ОДЗ:
ОДЗ:  На цій ОДЗ дане рівняння рівносильне рівнянням:
На цій ОДЗ дане рівняння рівносильне рівнянням:
 , ,
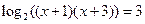 , ,
 , ,
 ,
х1 = 1, х2 = -5,
х1 = 1 – корінь (задовольняє умовам ОДЗ);
х2 = -5 – сторонній корінь (не задовольняє умовам ОДЗ).
Відповідь: 1. ,
х1 = 1, х2 = -5,
х1 = 1 – корінь (задовольняє умовам ОДЗ);
х2 = -5 – сторонній корінь (не задовольняє умовам ОДЗ).
Відповідь: 1.
|
Вправи
1. Розв'язати рівняння:
1)  ; ;
2) 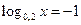 ; ;
3)  ; ;
4)  ; ;
5)  ; ;
6)  ; ;
7) 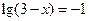 ; ;
8)  ; ;
9)  ; ;
10)  ; ;
11)  ; ;
12) 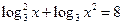 . .
Додаткові вправи
РОЗВ’ЯЗАННЯ ПОКАЗНИКОВИХ І ЛОГАРИФМІЧНИХ РІВНЯНЬ
- Розв'язати показникове рівняння:
- 4х = 64
-
 = 27 = 27 - 3х = 81
-
 = =  -
  = 225 = 225 -
  = 36 = 36 - (0,25) 2-х =
 -
 = =   | 1.   = =  2.
2. 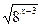 = =  3.
3.  = =  4.3х = 19х
4.3х = 19х
| 1.7х+2 + 4*7х+1 = 539
2. 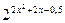 = 4 = 4  3.3х + 3х+1 = 108
4.4х+1 +4х = 320
5.2*3х+1 – 3х = 15
6.3*5х+3 + 2*5х+1 = 77
7.3х+1 2*3х-2 = 75
3.3х + 3х+1 = 108
4.4х+1 +4х = 320
5.2*3х+1 – 3х = 15
6.3*5х+3 + 2*5х+1 = 77
7.3х+1 2*3х-2 = 75
|
2. Розв'язати логарифмічне рівняння:
1.  = 2
2. = 2
2.  = -1
3. = -1
3.  = - = -  4.
4.  = 2
5. = 2
5.  = - 2
6. = - 2
6.  = 1
7. = 1
7.  = 0
9. = 0
9.  = 3 = 3
| 1.  = x
2. = x
2. 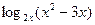 = =  3.
3.  = 0
4. = 0
4.  = = 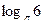 5.
5.  = 0
6. = 0
6. 
| 1.  2.
2.  3. log
3. log  (x+3) – log (x+3) – log  (x-1) = 2 - log (x-1) = 2 - log  8
4. 8
4.  = = 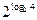
|
Тема. Розв’язання логарифмічних нерівностей
План
1. Графік функції у = loga x,  . .
2. Рівносильні перетворення найпростіших логарифмічних нерівностей.
1. Графік функції у = loga x,  . .
| 
| 
|  зростає
зростає
|  спадає
спадає
| | 2. Рівносильні перетворення найпростіших логарифмічних нерівностей
| 
| 
|

 Знак нерівності не змінюється,
і враховується ОДЗ
Знак нерівності не змінюється,
і враховується ОДЗ
|

 Знак нерівності змінюється,
і враховується ОДЗ
Знак нерівності змінюється,
і враховується ОДЗ
| | Приклади
|  .
ОДЗ: x – 5 > 0, тобто х > 5. .
ОДЗ: x – 5 > 0, тобто х > 5.
 Функція у =
Функція у =  зростаюча, тоді
х - 5 > 23,
х > 13.
Враховуючи ОДЗ, маємо х > 13.
Відповідь: (13; + зростаюча, тоді
х - 5 > 23,
х > 13.
Враховуючи ОДЗ, маємо х > 13.
Відповідь: (13; +  ). ).
|  .
ОДЗ: x – 5 > 0, тобто х > 5. .
ОДЗ: x – 5 > 0, тобто х > 5.
 Функція в =
Функція в =  спадна, тоді
х - 5 < спадна, тоді
х - 5 <  ,
х < 5 ,
х < 5  .
Враховуючи ОДЗ, маємо 5 < х < 5 .
Враховуючи ОДЗ, маємо 5 < х < 5  .
Відповідь: (5; 5 .
Відповідь: (5; 5  ). ).
| | 3. Розв’язання більш складних логарифмічних нерівностей
| | Орієнтир
| Приклад
| | І. За допомогою рівносильних перетворень дану нерівність приводять до нерівності відомого виду.
Схема рівносильних перетворень нерівності:
1. Ураховуємо ОДЗ заданої нерівності (і уникаємо перетворень, що приходять до звуження ОДЗ).
2. Стежимо за тим, щоб на ОДЗ кожне перетворення можна було виконати як у прямому, так і у зворотному напрямках із збереженням вірної нерівності
|  ОДЗ: x > 0. На цій ОДЗ дана нерівність рівносильна нерівностям:
ОДЗ: x > 0. На цій ОДЗ дана нерівність рівносильна нерівностям:
 , ,
 .
Заміна: .
Заміна:  . Тоді . Тоді 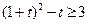 , тобто , тобто  . Рішення цієї нерівності . Рішення цієї нерівності
  або або  Обернена заміна дає
Обернена заміна дає
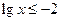 або або  .
Тоді .
Тоді
 або або  .
Враховуючи, що функція у = lg x є зростаючої, одержуємо: .
Враховуючи, що функція у = lg x є зростаючої, одержуємо:
 або або  .
За ОДЗ маємо: 0 < x .
За ОДЗ маємо: 0 < x  0,01 або 0,01 або  .
Відповідь: .
Відповідь:   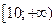 . .
| ІІ. Застосовується загальний метод інтервалів (дана нерівність приводиться до нерівності  , ,  ) і використовується схема:
1. Знайти ОДЗ;
2. Знайти нулі ) і використовується схема:
1. Знайти ОДЗ;
2. Знайти нулі 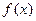 ;
3. Відзначити нулі функції на ОДЗ і знайти знак ;
3. Відзначити нулі функції на ОДЗ і знайти знак 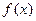 на кожному з проміжків, на які розбивається ОДЗ;
4. Записати відповідь, враховуючи знак нерівності. на кожному з проміжків, на які розбивається ОДЗ;
4. Записати відповідь, враховуючи знак нерівності.
|  Розв'яжемо нерівність методом інтервалів. Воно рівносильне нерівності
Розв'яжемо нерівність методом інтервалів. Воно рівносильне нерівності 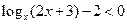 .
Позначимо .
Позначимо  .
1. ОДЗ: .
1. ОДЗ:  тобто тобто  2. Нулі функції:
2. Нулі функції:  . .  .
Тоді .
Тоді  . На ОДЗ це рівняння рівносильне рівнянню 2х + 3 = х2 (отриманому за означенням логарифма).
Тобто х2 - 2х - 3 = 0,
х1 = -1, х2 = 3.
В ОДЗ входить тільки х = 3. Отже, . На ОДЗ це рівняння рівносильне рівнянню 2х + 3 = х2 (отриманому за означенням логарифма).
Тобто х2 - 2х - 3 = 0,
х1 = -1, х2 = 3.
В ОДЗ входить тільки х = 3. Отже, 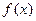 має єдиний нуль функції х = 3.
3. Відзначаємо нулі функції на ОДЗ, знаходимо знак має єдиний нуль функції х = 3.
3. Відзначаємо нулі функції на ОДЗ, знаходимо знак 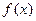 на кожному з проміжків, на які розбивається ОДЗ, і записуємо рішення нерівності на кожному з проміжків, на які розбивається ОДЗ, і записуємо рішення нерівності  . .
Відповідь: х  (0; 1) (0; 1)  (3; + (3; +  ) )
|
Вправи
Розв'язати нерівність
1)  ; ;
2)  ; ;
3)  ; ;
4)  ; ;
5)  ; ;
6)  ; ;
7)  ; ;
8)  ; ;
9)  ; ;
10)  ; ;
11)  ; ;
12)  . .
|
|
 = 2;
= 2; = 49;
= 49; =
= 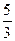 ;
; = 1;
= 1; = 3;
= 3; = 0, 008;
= 0, 008; = 8;
= 8; ;
; ;
; = 27;
= 27; = 3;
= 3; = 4;
= 4; =
=  ;
; =
= 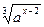 ;
; = 1;
= 1; = -2;
= -2; =
=  ;
; =
=  ;
; = 5
= 5  ;
; ;
; 3 = 81;
3 = 81; = 9.
= 9. =
=  ;
; =
=  ;
; =
=  ;
; =
=  ;
;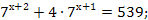



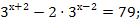
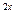 + 4 · 5
+ 4 · 5  -
-  = 3;
= 3; -
-  = 2;
= 2; +
+  = 5;
= 5; +
+  = 10;
= 10; +
+  = 80;
= 80; =
= 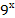 ;
;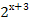 -
-  -
-  +
+  =
=  +
+  ;
; = 0;
= 0; ;
; = 0;
= 0; = 0;
= 0; = 0.
= 0. , де
, де  і
і  .
.


 зростає
зростає
 спадає
спадає
 >
> 
 f(x) > g(x)
знак нерівності зберігається
f(x) > g(x)
знак нерівності зберігається

 Функція у =
Функція у = 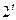 є зростаюча, отже:
х – 3 > 2,
х > 5.
Відповідь: (5; +
є зростаюча, отже:
х – 3 > 2,
х > 5.
Відповідь: (5; +  ).
).

 Функція в =
Функція в =  є спадною, отже:
є спадною, отже:

 .
Відповідь: (-
.
Відповідь: (- 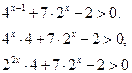
 Заміна
Заміна  дає нерівність
дає нерівність 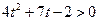 , розв’язання якого
, розв’язання якого  або
або  Обернена заміна дає
Обернена заміна дає  (розв’язаннь немає) або
(розв’язаннь немає) або 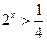 , звідки
, звідки  Відповідь: (-2; +
Відповідь: (-2; + 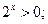
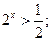
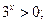
 ;
; ;
; ;
;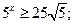
 ;
; .
. =
=  , тому що
, тому що  =
=  2,7).
Позначення: logе b = ln b
2,7).
Позначення: logе b = ln b
 = - 2, тому що е-2 =
= - 2, тому що е-2 =  a > 0,
a > 0,  ;
2)
;
2)  .
.

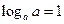



 (a > 0,
(a > 0, 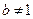 )
)


 = 4;
= 4; = 3;
= 3; ;
; ;
; ;
; = 3.
= 3. ;
;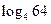 ;
; ;
; ;
; ;
; .
.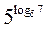 ;
;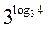 ;
; ;
; ;
; .
. :
: за основою 10;
за основою 10; за основою е;
за основою е; за основою 3.
за основою 3. ,
,  . Виразити через a і b:
. Виразити через a і b: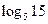 ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. .
.


 = loga u - loga v (u > 0, v > 0)
loga un = n loga u
= loga u - loga v (u > 0, v > 0)
loga un = n loga u
 =
= 

 ;
; ;
; ;
; .
. ;
; ;
;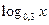 ;
; ;
; ;
; ;
; ;
; ;
;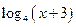 ;
; ;
; .
. і
і  ;
;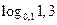 і
і  ;
; і
і  ;
; і
і  ;
; і 0;
і 0; і 1.
і 1. (використовуємо визначення логарифма)
(використовуємо визначення логарифма)
 х – 1 = 32,
х = 9 + 1,
х = 10.
Відповідь: 10
х – 1 = 32,
х = 9 + 1,
х = 10.
Відповідь: 10
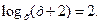 За визначенням логарифма одержуємо
х + 2 = х2,
х2 – х – 2 = 0,
х1 = -1, х2 = 2.
Перевірка: х = -1 – сторонній корінь (в основі логарифма одержуємо від’ємне число); х = 2 – корінь, тому що
За визначенням логарифма одержуємо
х + 2 = х2,
х2 – х – 2 = 0,
х1 = -1, х2 = 2.
Перевірка: х = -1 – сторонній корінь (в основі логарифма одержуємо від’ємне число); х = 2 – корінь, тому що
 Відповідь: 2
Відповідь: 2
 .
Заміна:
.
Заміна:  ,
,
 ,
,
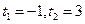 .
Отже,
.
Отже, 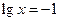 або
або  .
Тоді х = 10-1 = 0,1 або х = 103 = 1000.
Відповідь: 0,1; 1000.
.
Тоді х = 10-1 = 0,1 або х = 103 = 1000.
Відповідь: 0,1; 1000.
 (
(  (враховуємо ОДЗ і дорівнюємо вирази, які стоять під знаками логарифмів)
(враховуємо ОДЗ і дорівнюємо вирази, які стоять під знаками логарифмів)
 ОДЗ:
ОДЗ: 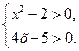 На цій ОДЗ дане рівняння рівносильне рівнянням: х2 – 2 = 4х – 5,
х2 – 4х + 3 = 0,
х1 = 1, х2 = 3,
х1 = 1 – сторонній корінь (не задовольняє умовам ОДЗ);
х2 = 3 – корінь (задовольняє умовам ОДЗ).
Відповідь: 3
На цій ОДЗ дане рівняння рівносильне рівнянням: х2 – 2 = 4х – 5,
х2 – 4х + 3 = 0,
х1 = 1, х2 = 3,
х1 = 1 – сторонній корінь (не задовольняє умовам ОДЗ);
х2 = 3 – корінь (задовольняє умовам ОДЗ).
Відповідь: 3
 ОДЗ:
ОДЗ:  На цій ОДЗ дане рівняння рівносильне рівнянням:
На цій ОДЗ дане рівняння рівносильне рівнянням:
 ,
,
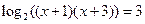 ,
,
 ,
,
 ,
х1 = 1, х2 = -5,
х1 = 1 – корінь (задовольняє умовам ОДЗ);
х2 = -5 – сторонній корінь (не задовольняє умовам ОДЗ).
Відповідь: 1.
,
х1 = 1, х2 = -5,
х1 = 1 – корінь (задовольняє умовам ОДЗ);
х2 = -5 – сторонній корінь (не задовольняє умовам ОДЗ).
Відповідь: 1.
 ;
;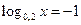 ;
; ;
; ;
; ;
; ;
;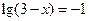 ;
; ;
; ;
; ;
; ;
;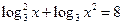 .
. = 27
= 27 =
= 

 = 225
= 225

 =
= 


 =
=  2.
2. 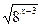 =
=  3.
3.  =
=  4.3х = 19х
4.3х = 19х
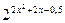 = 4
= 4  3.3х + 3х+1 = 108
4.4х+1 +4х = 320
5.2*3х+1 – 3х = 15
6.3*5х+3 + 2*5х+1 = 77
7.3х+1 2*3х-2 = 75
3.3х + 3х+1 = 108
4.4х+1 +4х = 320
5.2*3х+1 – 3х = 15
6.3*5х+3 + 2*5х+1 = 77
7.3х+1 2*3х-2 = 75
 = 2
2.
= 2
2.  = -1
3.
= -1
3.  = -
= -  4.
4.  = 2
5.
= 2
5.  = - 2
6.
= - 2
6.  = 1
7.
= 1
7.  = 0
9.
= 0
9.  = 3
= 3
 = x
2.
= x
2. 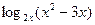 =
=  3.
3.  = 0
4.
= 0
4.  =
= 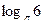 5.
5.  = 0
6.
= 0
6. 
 2.
2.  3. log
3. log  (x+3) – log
(x+3) – log  =
= 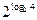
 зростає
зростає
 спадає
спадає

 Знак нерівності не змінюється,
і враховується ОДЗ
Знак нерівності не змінюється,
і враховується ОДЗ

 Знак нерівності змінюється,
і враховується ОДЗ
Знак нерівності змінюється,
і враховується ОДЗ
 .
ОДЗ: x – 5 > 0, тобто х > 5.
.
ОДЗ: x – 5 > 0, тобто х > 5.
 Функція у =
Функція у =  зростаюча, тоді
х - 5 > 23,
х > 13.
Враховуючи ОДЗ, маємо х > 13.
Відповідь: (13; +
зростаюча, тоді
х - 5 > 23,
х > 13.
Враховуючи ОДЗ, маємо х > 13.
Відповідь: (13; +  .
ОДЗ: x – 5 > 0, тобто х > 5.
.
ОДЗ: x – 5 > 0, тобто х > 5.
 Функція в =
Функція в =  спадна, тоді
х - 5 <
спадна, тоді
х - 5 <  ,
х < 5
,
х < 5  .
Враховуючи ОДЗ, маємо 5 < х < 5
.
Враховуючи ОДЗ, маємо 5 < х < 5  ОДЗ: x > 0. На цій ОДЗ дана нерівність рівносильна нерівностям:
ОДЗ: x > 0. На цій ОДЗ дана нерівність рівносильна нерівностям:
 ,
,
 .
Заміна:
.
Заміна: 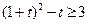 , тобто
, тобто  . Рішення цієї нерівності
. Рішення цієї нерівності

 або
або  Обернена заміна дає
Обернена заміна дає
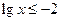 або
або  .
Тоді
.
Тоді
 або
або  .
Враховуючи, що функція у = lg x є зростаючої, одержуємо:
.
Враховуючи, що функція у = lg x є зростаючої, одержуємо:
 або
або  .
За ОДЗ маємо: 0 < x
.
За ОДЗ маємо: 0 < x  0,01 або
0,01 або 

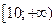 .
.
 ,
,  ) і використовується схема:
1. Знайти ОДЗ;
2. Знайти нулі
) і використовується схема:
1. Знайти ОДЗ;
2. Знайти нулі 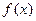 ;
3. Відзначити нулі функції на ОДЗ і знайти знак
;
3. Відзначити нулі функції на ОДЗ і знайти знак  Розв'яжемо нерівність методом інтервалів. Воно рівносильне нерівності
Розв'яжемо нерівність методом інтервалів. Воно рівносильне нерівності 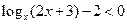 .
Позначимо
.
Позначимо  .
1. ОДЗ:
.
1. ОДЗ:  тобто
тобто  2. Нулі функції:
2. Нулі функції:  .
.  .
Тоді
.
Тоді  . На ОДЗ це рівняння рівносильне рівнянню 2х + 3 = х2 (отриманому за означенням логарифма).
Тобто х2 - 2х - 3 = 0,
х1 = -1, х2 = 3.
В ОДЗ входить тільки х = 3. Отже,
. На ОДЗ це рівняння рівносильне рівнянню 2х + 3 = х2 (отриманому за означенням логарифма).
Тобто х2 - 2х - 3 = 0,
х1 = -1, х2 = 3.
В ОДЗ входить тільки х = 3. Отже, 
 (0; 1)
(0; 1)  ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.