Особенности ввода команд и данных

Команды вводятся в окне Command Window в командной строке после приглашения системы >>. Для выполнения введенной команды надо нажать клавишу <Enter>. Для хранения выполненных команд предусмотрен кольцевой буфер. Для просмотра и выбора предыдущих команд используются клавиши управления:
­ и ¯. Все выполненные команды можно видеть в окне Command History. Любую предыдущую команду можно вызвать для исполнения, дважды щелкнув по ее отображению в этом окне.

В ML строчные и прописные буквы различаются. Это надо учитывать при записи команд. Принято обозначать все векторы и матрицы прописными(большими)буквами, функции – строчными(маленькими).

Если команда при наборе не помещается в строку, то в конце строки ставятся три точки (…) без пробелов, затем нажимается <Enter> и дальше набор продолжается с новой строки.

Результат выполнения каждой команды сразу отображается на экране. Если в конце строки (после команды) стоит точка с запятой, то результат не будет выведен на экран.При желании можно вводить несколько команд в одной строке, разделяя их точкой с запятой.

Простейший способ работы в ML – это режим прямых вычислений (режим калькулятора).Команды выполняются сразу после их ввода, а результат выводится сразу после выполнения команды.

Например, вводим команду:

>> sin(0.5)

Нажимаем <Enter>

Получаем ответ:

ans =

0.4794

Вводим команду:

>> 3^2-(5+4)/2+6*3

Нажимаем <Enter> и получаем ответ:

ans =

22.5000

ML вычисляет выражение, помещает его в специальную переменную ans и выводит полученное значение в отдельной строке.

Текущий сеанс работы пользователя с системой Matlab называют сессией.

Элементы данных в ML

Все данные в ML интерпретируются как массивы. Массив – это упорядоченный набор однородных данных. Элементами массива могут быть целые, вещественные, комплексные числа и символы. Каждый массив имеет имя и характеризуется числом измерений и количеством элементов по каждому измерению. Доступ к элементу массива осуществляется указанием имени и индексов. Нумерация элементов начинается с единицы по каждому измерению.

Основной элемент данных в ML – матрица. Числа и векторы рассматриваются как вырожденные матрицы. Например, число – это матрица размером 1×1. Векторы – это матрицы с одним столбцом или с одной строкой.

Числа в ML могут быть целыми, вещественными, комплексными. Целые числа вводятся в обычной форме. Вещественные числа могут записываться в естественной форме с фиксированной точкой (2.5) и в экспоненциальной (3.4е-3). При вводе между цифрами числа не допускаются пробелы.

Форматы представления результатов вычислений

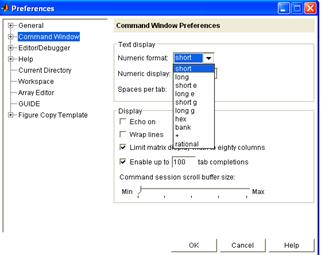
Вид результатов вычислений зависит от установленного формата вывода. Пользователь может задавать различные форматы представления чисел. По умолчанию установлен формат short (4 цифры после десятичной точки) –краткое представление числа.

Установить другой формат можно, если выбрать пункт меню File, Preferences, Numeric format (формат числа), OK. Этот формат будет использоваться для вывода результатов всех последующих вычислений, пока не будет изменен (рис. 4).

Рис. 4

Некоторые форматы: long (14 цифр) – длинное представление числа с фиксированной точкой, short e (четыре значащих цифры мантиссы и три знака порядка)–краткое представление числа в экспоненциальной форме, long e – длинное представление числа в экспоненциальной форме, long g –выбирает наиболее удачное представление для числа, bank (2 цифры после десятичной точки) – представление для денежных сумм и т.д.

Управлять форматом можно не только с помощью меню. Этого же результата можно достичь, если ввести в командную строку команду: format <формат>.

Например,

>> format long

>> 7/8

ans =

0.87500000000000

>> format long g

>> 7/8

ans =

0.875

>> format long e

>> 7/8

ans =

8.750000000000000e-001

Для получения информации обо всех форматах необходимо ввести в командную строку команду: help format.

Переменные в ML

В ML, как и в других языках программирования, существует возможность работы с переменными. Любая переменная до использования в формулах должна быть определена. Для этого надо присвоить ей значение. Типы переменных заранее не объявляются. Тип определяется значением, которое присваивается переменной. В качестве оператора присваивания используется знак равенства(=):

>> n=5

n =

>> k=0.5

k =

0.5000

По типу переменные могут быть числовыми (целые, вещественные, комплексные) или символьными.

Правила составления идентификаторов такие же, как и в ЯВУ (начинается с буквы и может содержать любые комбинации цифр, букв, символа подчеркивания, идентифицируются первые 63 символа, нельзя использовать специальные символы и пробелы, имя переменной должно быть уникальным и не совпадать с именами функций). Следует помнить, что строчные и прописные буквы различаются(Abc и abc – разные имена).

Существуют встроенные системные переменные, которые можно использовать, не задавая значения. Они при необходимости могут быть переопределены, т.е. им можно присвоить другие значения, но тогда значения, заданные по умолчанию, будут утеряны:

· pi – число p(p=3.141592653589793);

· eps – погрешность операций над числами с плавающей точкой; очень маленькое значение, равное 2.2*10^-16. Её используют, когда надо исключить деление на 0 (например, x/(y+eps));

· ans – результат последней команды, если в ней нет операции присваивания. Например, если набрали команду 41/75 и не определили, какой переменой присвоить результат, на экране отобразится ans = 0.5467;

· nan – для обозначения неопределённости результата;

· i, j – мнимая единица( ), используемая для задания мнимой части комплексного числа. Задать комплексные числа можно так: z = 3+4i.

Все эти переменные можно использовать в математических выражениях.

В ML все переменные занимают определенное место в памяти, называемой рабочим пространством системы – Workspace.

ML запоминает значения всех переменных, используемых в текущей сессии. Для того чтобы узнать, какие переменные были задействованы, используется команда who. Чтобы получить более подробную информацию о переменных: размеры, размерность, можно использовать команду whos. Эту информацию можно увидеть и в окне Workspace.

Для удаления из памяти всех переменных используется команда clear.

Выборочное удаление переменных можно сделать, применив команду Clear следующим образом: Clear a b.

После завершения сессии ML все переменные рабочего пространства, определенные в текущем сеансе работы, будут потеряны. При необходимости можно сохранить значения переменных в файле. Для этого нужно выбрать пункт меню File, Save Workspace As, далее в диалоговом окне задать имя файла для сохранения данных. Результаты будут сохранены в бинарном файле с расширением mat. Для восстановления значений переменных в следующем сеансе работы необходимо выбрать File, Oреn, имя файла. В результате все переменные станут доступны.

Другой способ сохранения и восстановления переменных рабочего пространства – набрать команды:

Save <имя файла.mat> и Load <имя файлa.mat> соответственно.

Всю сессию (все, что отображается в командном окне) можно сохранить и поместить в текстовый файл. Для этого необходимо выполнить следующую команду:

diary <имя>.txt

Эта команда начинает запись сессии в текстовый файл. По команде diary off запись прекращается. Команда diary on возобновляет запись.

Задание векторов и матриц

Способы задания векторов

Вектор – это одномерный массив данных. Вектор в ML – это матрица из одного столбца или одной строки. Соответственно вектор может быть вектором-столбцом или вектором-строкой.

Для задания вектора можно воспользоваться одним из приведенных ниже способов.

1. Можно задать значения вектора поэлементно:

<имя пер.>=[<значение1> <значение2> ….<значениеN>]

Например,

>>P=[3 5 7 12]

Значения элементов записываются через пробел или через запятую.

В результате выполнения этой команды создается вектор-стро-ка:

P =

3 5 7 12

Если при задании вектора значения его элементов разделить точкой с запятой, то получим вектор-столбец:

<<A=[1; 2; 3]

A=

2. Если элементы вектора являются арифметической прогрессией, то можно задать вектор так:

<имя пер.>=<нач. значение>:<шаг>:<конечное значение>

Например,

>>X=0 : 0.5: pi

В результате будет сформирован вектор со значениями:

X =

0 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000

Шаг должен быть больше нуля. Если он равен единице, то его можно не указывать:

>>Х = 1 : 10

X =

1 2 3 4 5 6 7 8 9 10

Чтобы изменить форму вектора, надо записать Х’ – тогда вектор отобразится в виде столбца. Такая операция называется транспонированием.

Например,

>> X=1:1:5

X = 1 2 3 4 5

>> X'

ans =

3. Также для формирования арифметической прогрессии можно использовать функцию linspace:

Задание матриц

При задании матриц данные строк записываются через пробел или через запятую. Элементы разных строк разделяются знаком точка с запятой (;) или записываются с новой строки. В ML матрица хранится в порядке следования по столбцам.

Зададим матрицу:

>>A=[1 2 3; 4 5 6;7 8 9]

A =

1 2 3

4 5 6

7 8 9

или

>> A=[1 2 3

4 5 6

7 8 9]

A =

1 2 3

4 5 6

7 8 9

Обращение к элементу матрицы: <имя> (<индексы>), например, А(2,3).

Операции

В MLможно не только выполнять обычные арифметические операции над числами и вычислять значения функций, но и производить операции над векторами и матрицами.