|
|
ЗАСТОСУВАННЯ ТА АНАЛІЗ МЕТОДІВ ЧИСЕЛЬНОГО ІНТЕГРУВАННЯ
5.1 Мета роботи
Застосування чисельних методів обчислення інтегралів у різноманітних практичних задачах. Аналіз та порівняння результатів.
5.2 Організація самостійної роботи
До лабораторної роботи за конспектом лекцій та [1–4] вивчити теоретичний матеріал щодо розв’язання задач чисельного інтегрування за допомогою формул Ньютона-Котеса та їх основних окремих випадків – формул трапецій та Симпсона.
5.3 Склад лабораторного устаткування
Лабораторна робота виконується на обчислювальному комплексі, у складі якого: локальна обчислювальна мережа комп'ютерів типу IBM PC, Windows XP.
5.4 Порядок виконання роботи
1. Вибрати варіант індивідуального завдання з табл. 5.1 згідно з номером n студента у списку групи.
Таблиця 5.1 – Варіанти індивідуальних завдань
2. Користуючись навичками інтегрування, обчислити інтеграл
в елементарних функціях та отримати точний розв’язок задачі. 3. Розробити алгоритм методу чисельного інтегрування за допомогою формул трапецій та Симпсона і запрограмувати засобами однієї з алгоритмічних мов. За допомогою розробленої програми знайти два значення інтегралу (5.1) відповідно за допомогою формул трапецій та Симпсона. 4. Задаючись різними значеннями параметра закінчення ітераційного процесу в процедурі чисельного інтегрування, виконати п.3 декілька разів. У кожному випадку оцінити похибку інтегрування двома способами: - як модуль різниці між точним та наближеним значеннями інтегралу; - користуючись відповідними формулами для похибок формул трапецій та Симпсона. Результати обчислювальних експериментів занести в таблицю. 5. Зробити висновки з роботи, оформити індивідуальний звіт.
5.5 Зміст звіту
Звіт має містити: 1. Індивідуальне завдання до роботи. 2.Результати аналітичного розв’язання задачі інтегрування. 3. Алгоритм методу чисельного інтегрування. 4. Роздруківку програми. 5. Результати обчислювального експерименту. 6. Аналіз отриманих результатів і висновки з роботи.
5.6 Контрольні запитання і завдання
1. Що є чисельним розв’язком задачі чисельного інтегрування? 2. Яким чином побудовано квадратурні формули Ньютона-Котеса? 3. Як побудовано формулу трапецій? 4. Як побудовано формулу Симпсона? 5. Наведіть спосіб оцінки похибок квадратурних формул трапецій та Симпсона. 6. Як залежить величина похибки квадратурної формули від величини кроку інтегрування? 7. Як залежить величина похибки квадратурної формули від ступеня інтерполяційного полінома? ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ ЗВИЧАЙНИХ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ
6.1 Мета роботи
Формування навичок практичного застосування чисельних методів розв’язання звичайних диференціальних рівнянь (ЗДР).
6.2 Організація самостійної роботи
Вивчити теоретичний матеріал за темою “Методи розв’язання звичайних диференціальних рівнянь” [1, 3, 4], приділивши увагу методам Рунге-Кутта, модифікованому Ейлера, виправленому Ейлера.
6.3 Склад лабораторного устаткування
Лабораторна робота виконується на обчислювальному комплексі, у складі якого: локальна обчислювальна мережа комп'ютерів типу IBM PC, Windows XP.
6.4 Порядок виконання роботи
1. Отримати індивідуальний варіант вхідних даних до роботи: рівняння і метод вирішення задачі (табл. 6.1) згідно з номером студента у списку групи.
Таблиця 6.1 – Варіанти індивідуальних завдань
Продовження табл. 6.1
Примітка до табл. 6.1: РК – метод Рунге-Кутта МЕ – модифікований метод Ейлера ВЕ – виправлений метод Ейлера. 2. Розробити алгоритм методу вирішення ЗДР і запрограмувати його засобами обраної алгоритмічної мови. Розв’язати рівняння, використовуючи програму. При цьому задати кількість точок n =10, а крок за змінною 3. Зменшити крок за змінною до h= 0,1 і побудувати 20 точок розв’язку. 4. Результати двох розв’язків показати у вигляді графіків 5. Оформити індивідуальний звіт з роботи.
6.5 Зміст звіту
Звіт має містити: 1. Постановку задачі. 2. Схему методу вирішення ЗДР. 3. Результати розв’язків при n=10, h=0,2, n=20,h=0,1. 4. Графічне зображення залежності 5. Результати порівняльного аналізу і висновки з роботи.
6.6 Контрольні запитання і завдання
1. Що є звичайним диференціальним рівнянням? 2. Що називається початковою умовою звичайного диференціального рівняння? 3. Що є розв’язком звичайного диференціального рівняння? 4. Які методи розв’язання диференціальних рівнянь належать до одноступеневих, а які до багатоступеневих? 5. В чому суть методу Ейлера та його модифікацій? 6. Наведіть оцінки точності методів розв’язання звичайних диференціальних рівнянь. ПЕРЕЛІК ПОСИЛАНЬ
1. Фельдман Л.П, Петренко А.І., Дмитрієва О.А. Чисельні методи в інформатиці. –К.: Видавнича група BHV, 2006. –480 с. 2. Демидович Б.П. Основы вычислительной математики. – М.: Наука. – 1966. –664 с. 3. Волков Е.А. Численные методы. – М.: Наука .– 1987. –254 с. 4. Ляшенко М.Я., Головань М.С.Чисельні методи.-К.:Либідь,1996. – 288 с.
Навчальне видання
МЕТОДИЧНІ ВКАЗІВКИ до лабораторних робіт з дисципліни "ЧИСЕЛЬНІ МЕТОДИ" для студентів денної форми навчання напрямів 6.050101 „Комп’ютерні науки”, 6.050201 „Системна інженерія”, 6.050202 „Автоматизація та комп’ютерно-інтегровані технології”
Упорядник: ГРЕБЕННІК Ігор Валерійович КАЛИТА Надія Іванівна
Відповідальний випусковий Е.Г. Петров
Редактор Н.А. Крижна Комп’ютерна верстка Н.Є. Сіпатова
План 2012 (друге півріччя), поз. _.
Підп. до друку 00.00.12 Формат 60х84 1/16. Спосіб друку - ризографія Умов. друк. арк. 0,9 Облік.-вид. арк. 0,8 Тираж 75 прим. Зам. № 1-52 Ціна договірна. ----------------------------------------------------------------------------------------- ХНУРЕ. Україна. 61166 Харків, просп. Леніна, 14 -----------------------------------------------------------------------------------------
Віддруковано в навчально-науковому видавничо-поліграфічному центрі ХНУРЕ 61166, Харків, просп. Леніна, 14. 12 |
|






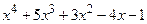




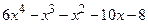




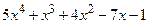








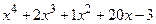




 (5.1)
(5.1)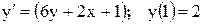




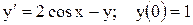
















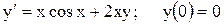

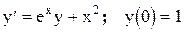



 h =0,2.
h =0,2. в одній системі координат. Порівняти і проаналізувати обидва розв’язки.
в одній системі координат. Порівняти і проаналізувати обидва розв’язки.