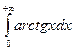|
|
Медико-биологического факультетаМетодические указания К проведению практических занятий по математике (математическому анализу) для студентов 2-го курса отделения Биотехнические системы и технологии Медико-биологического факультета Семестр 2 БСТ-1к2с(МА) К занятию «Утверждаю» зав. кафедрой З.А. Филимонова Методические указания № 1 К проведению практического занятия по математике (математическому анализу) для студентов 1-го курса отделения биотехнические системы и технологии Медико-биологического факультета
Тема: «Определенный интеграл». Цель: проверить знание теоретического материала и умения применять его при решении различных задач 1. Основные вопросы темы: 1) Задачи, приводящие к понятию определенного интеграла; 2) Понятие определенного интеграла. Пределы интегрирования. Формула Ньютона-Лейбница; 3) Свойства определенного интеграла; 4) Формулы замены переменной и интегрирования по частям в определенном интеграле; 2. Самостоятельная работа студентов 1) Повторить основные методы нахождения неопределенных интегралов. 2) Подготовить основные вопросы темы. 3) Выучить свойства определенного интеграла и таблицу неопределенных интегралов 4) Решите задачи (в тетради для домашних работ): Найдите неопределенные интегралы: 1)
Вычислите определенные интегралы: 1) 2) 3) 4) 5) 6) 7)
3. Содержание аудиторной работы: - проверить выполнение домашнего задания - решать задачи по теме занятия (подбираются на усмотрение преподавателя) - выполнить самостоятельную работу по теме занятия.
& ЛИТЕРАТУРА: 1. Данко П. Е. и др. Высшая математика в упражнениях и задачах, Ч.1 Гл.X § 1 2. Пискунов Н.С. Дифференциальное и интегральное исчисление, Т.1 Гл.XI §§ 1-6 3.Лекции
Метод. указание составлено Т.П.Сопит
БСТ-1к2с(МА) К занятию «Утверждаю» зав. кафедрой З.А. Филимонова Методические указания № 2 К проведению практического занятия по математике (математическому анализу) для студентов 1-го курса отделения биотехнические системы и технологии Медико-биологического факультета
Тема: «Практические приложения определенного интеграла». Цель: проверить знание теоретического материала и умения применять его при решении различных задач 1. Основные вопросы темы:
1) Приложения определенного интеграла к геометрии: · Вычисление площадей плоских фигур; · Вычисление длины дуги кривой; · Вычисление объема тела вращения; · Вычисление площади поверхности тела вращения 2) Приложения определенного интеграла к физике: ¨ Вычисление работы переменной силы; ¨ Нахождение статических моментов и моментов инерции плоской дуги; ¨ Нахождение статических моментов и моментов инерции криволинейной трапеции; ¨ Нахождение координат центра тяжести однородной дуги плоской кривой; ¨ Нахождение координат центра тяжести криволинейной трапеции.
2. Самостоятельная работа студентов 1) Подготовить основные вопросы темы (записать основные формулы в тетрадь для практических работ). 2) Решите задачи (в тетради для домашних работ): - (1) Вычислить площади фигур, ограниченных линиями: а) замечание: к решению прилагать схематические графики, требуемые площади на рисунках выделять штриховкой.
- (2)Данко П.Е. «Высшая математика в упражнениях и задачах»: С. 253 (1604), С.255 (1615), С.266 (№ 1679), С.260 (№ 1645), С.262 (1654). -
3. Содержание аудиторной работы: - проверить выполнение домашнего задания - решать задачи по теме занятия (подбираются на усмотрение преподавателя) - выполнить самостоятельную работу по теме занятия.
& ЛИТЕРАТУРА: 1. Данко П. Е. и др. Высшая математика в упражнениях и задачах, Ч.1 Гл.X §§ 3-9 2. Пискунов Н.С. Дифференциальное и интегральное исчисление, Т.1 Гл.XII §§ 1-9 3. Лекции
Метод. указание составлено Т.П.Сопит
БСТ-1к2с(МА) К занятию «Утверждаю» зав. кафедрой З.А. Филимонова Методические указания № 3 К проведению практического занятия по математике (математическому анализу) для студентов 1-го курса отделения биотехнические системы и технологии медико-биологического факультета
Тема: «Несобственные интегралы. Несобственные интегралы с бесконечными пределами и от неограниченных функций. Их основные свойства». Цель:рассмотреть несобственные интегралы различных видов, научить решать вопрос о сходимости данного несобственного интеграла, 1. Основные вопросы темы:
1) Интеграл с бесконечными пределами; 2) Интеграл от неограниченных функций (от разрывных функций); 3) Признаки сходимости определенных интегралов. 2. Самостоятельная работа студентов 3) Подготовить основные вопросы темы (записать основные формулы в тетрадь для практических работ). 4) Решите задачи (в тетради для домашних работ): Исследуйте на сходимость интегралы: 1. 2. 3. 4. 5. 6.
3. Содержание аудиторной работы: - проверить выполнение домашнего задания - выполнить самостоятельную работу; - решать задачи по теме занятия (подбираются на усмотрение преподавателя).
& ЛИТЕРАТУРА:
Метод. указание составлено Т.П.Сопит
БТСТ-1к2с(Мат.Ан) к занятию Утверждаю зав.кафедрой З.А.Филимонова
Методические указания № 4-5 |
|
 ; 2)
; 2)  ; 3)
; 3)  .
. ;
; ;
; ;
; ;
; ;
; ;
;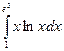 .
. ; б)
; б) 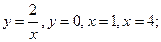
 ;
; ;
;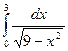
 ;
;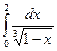 ;
;