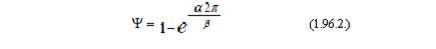|
|
Типовые звенья систем управленияЭлементарные звенья, из которых состоит система автоматического управления, имеют различные принципы действия и конструктивные особенности. Для удобства проектирования, анализа систем, применяются типовые виды элементарных звеньев, имеющие определенные динамические параметры. Данные звенья соединяют в требуемую структурную схему, и в зависимости от их характеристик получают необходимые выходные параметры системы. Характеристиками звеньев являются дифференциальные уравнения, описывающие процессы, происходящие в звене во время переходного процесса. Система автоматического управления может состоять из звеньев, использующих различные виды энергии (пар, вода, тепло, ветер, электричество, атомная энергия и т.д.) и различное конструктивное исполнение (электродвигатель, реле, датчики давления, датчики уровня, преобразователи, регуляторы температуры и т.д.). Независимо от перечисленных различий переходные процессы в звеньях могут описываться одними и теми же дифференциальными уравнениями, так как схожие динамические параметры различных звеньев позволяют объединить их в типовые группы. Создание классификации типовых звеньев, выделение типовых групп из их большого количества позволило упростить создание реальных систем автоматического управления, их проектирование и расчет. Элементарное звено – неделимое звено, имеющее по одному входу и выходу, описываемое дифференциальным уравнением не выше второго порядка и пропускающее сигнал только в одном направлении. Наиболее удобно классифицировать типовые звенья, используя частные формы линейного дифференциального уравнения второго порядка, представленного ниже:
a0 y′′( t) + a1 y′(t) + a2 y(t) = b0 x′(t) + b1 x(t) (1.63.)
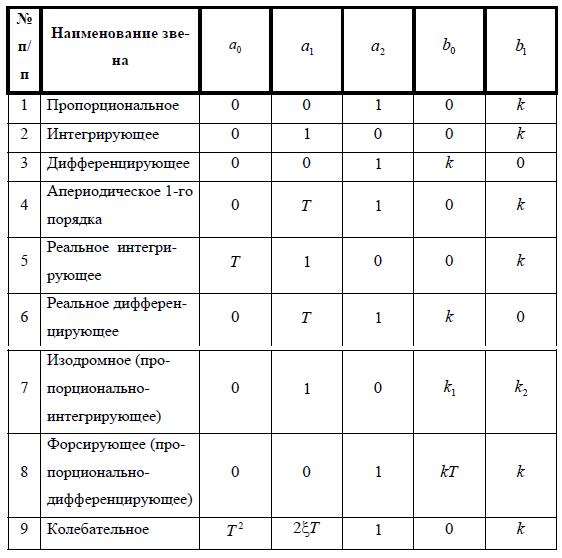
При изменении коэффициентов a и b изменяется уравнение состояния, и в свою очередь изменяется вид (тип) описываемого данным уравнением звена. В таблице изменения характеристик типовых звеньев САУ, в зависимости от изменения коэффициентов дифференциального уравнения, на рисунке 27.1. приведены виды звеньев, реализация которых имеет физический смысл (1.63.). Представленные звенья имеют общие особенности. Звенья, у которых коэффициенты a2 ≠ 0 и b1 ≠ 0, обладают однозначной связью между входом и выходом в статическом режиме. Поэтому их называют статическимиили позиционными. К этим звеньям относятся звенья, расположенные в таблице под №№ 1, 3, 4, 6, 8 и 9. Звенья под №№ 2, 5, 7 называют астатическими. Звенья, у которых a2 ≠ 0 и a1 ≠ 0 или a0 ≠ 0 (№ 4, 6, 9) обладают инерционностью (замедлением). Звенья № 1, 2 и 3 имеют только два коэффициента не равные нулю, поэтому считаются элементарными. Все остальные звенья могут быть образованы из элементарных звеньев путем комбинирования.
Рис.27.1 Таблица изменения характеристик типовых звеньев САУ, в зависимости от изменения коэффициентов дифференциального уравнения
Подробнее рассмотрим виды типовых звеньев, т.к. знание их характеристик существенно облегчает анализ и синтез САУ, потому что любой элемент системы и вся система в целом могут быть представлены в виде одного или совокупности типовых звеньев.
1.8.1. Пропорциональное (безынерционное) звено
Подставив в уравнение (1.63) значения bо = 0 и a1 = a2 = 0, получим уравнение состояния следующего вида:
где выходной параметр пропорционален входному. Звено, процессы в котором описываются указанным уравнением состояния, называется пропорциональным или безынерционным. Передаточную функцию безынерционного звена можно найти, применив к выражению (1.64.) прямое преобразование Лапласа. После преобразования получаем:
В данном случае k – передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к размерности входного. Переходная функция звена h(t) имеет следующее представление:
Импульсная переходная характеристика будет выглядеть:
w(t) = h′(t) = kδ (t)(1.67.)
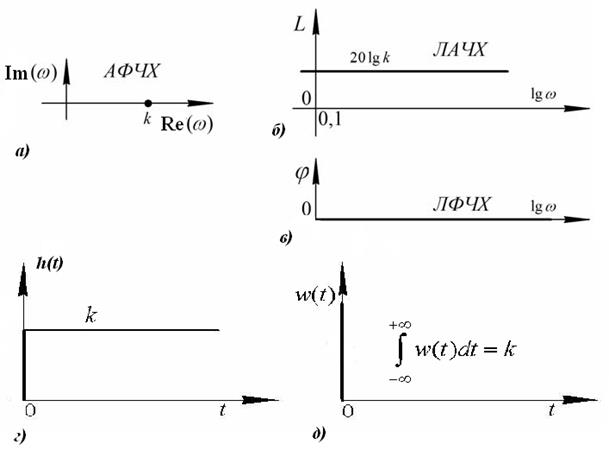
Графическое представление характеристик звена изображено на рисунке 28.
Рис.28. Характеристики пропорционального звена: а), б), в) – частотные; г), д), - временные. Пропорциональное (безынерционное) звено можно охарактеризовать равномерным пропусканием всех частот с отсутствием сдвига по фазе. Совпадение по фазе выходных колебаний с входными называют синфазностью. Реальные звенья все же обладают инерционностью, поэтому относятся к типу пропорциональных (безынерционных) условно, т.к. инерционность звена считается незначительной, если его инерционность пренебрежительно мала относительно инерционности всей системы. К типу таких реальных пропорциональных звеньев могут быть отнесены червячные редукторы, рычажные сочленения, усилители и т.д. Реальное представление пропорционального звена изображено на рисунке 29.
Рис.29. Реальные представления пропорционального (безынерционного) звена
Интегрирующее звено Подставив в уравнение (1.63) значения b0 = 0 и a0 = a2 = 0, получим уравнение состояния следующего вида (дифференциальное уравнение первого порядка):
a1 y′(t) = b1 x(t) (1.68.)
Выходной параметр звена пропорционален интегралу его входного параметра и описывается следующим выражением:
Передаточная функция интегрирующего звена может быть найдена с помощью преобразования по Лапласу и будет иметь вид:
В данном случае k – передаточный коэффициент звена, размерность которого определяется отношением размерности скорости изменения выходного параметра к размерности входного. Переходная функция звена при х(t) = 1(t) имеет следующее представление:
В данном случае С – постоянная интегрирования, при начальных условиях равная нулю. При постоянном параметре входного воздействия выходной параметр может изменяться, т.к. постоянная интегрирования может принимать различные значения, поэтому интегрирующее звено называют астатическим. Если величина входного параметра уменьшится до нуля, то, в отличие от пропорционального звена, в интегрирующем звене величина выходного параметра не будет стремиться к нулю. Интегрирующее звено также называют интегратором. Для получения АФЧХ интегрирующего звена подставим в выражение (1.70.) jwвместо р, и получим:
Из выражения видно, что действительная частотная характеристика Re(w) равна нулю, при этом мнимая частотная характеристика совпадет с АЧХ:
Далее, найдем ФЧХ интегрирующего звена следующим образом:
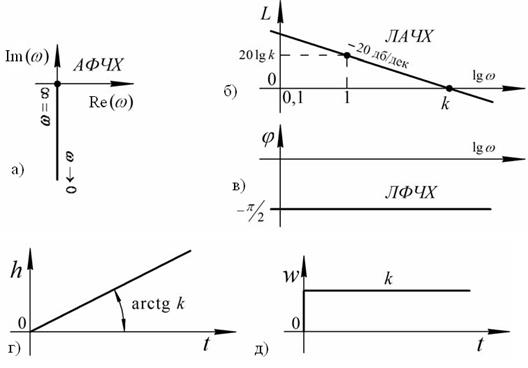
Из этого следует, что интегратор ослабляет высокие частоты и неограниченно усиливает низкие частоты. Амплитуда выходных колебаний стремится к нулюс ростом частоты входных колебаний, при этом сдвиг фаз постоянен и равен – π/2. Графическое представление характеристик звена изображено на рисунке 30.
Рис.30. Характеристики интегрирующего звена: а), б), в) – частотные; г), д), - временные
Существующие реальные интегрирующие звенья характеризуются «накапливанием» входного воздействия и обладают заметной инерционностью. Интегрирующее звено не может находиться в состоянии равновесия при любом постоянном значении входного сигнала. При воздействии любой минимальной величины входного параметра, величина выходного параметра через некоторое время может стать несоизмеримо большой. Положение равновесия в данном звене достигается только при отсутствии входного воздействия. Примерами существующих звеньев может служить конденсатор (электрическая емкость), гидравлический демпфер и т.д. Схема реального представления интегрирующего звена изображена на рисунке 31.
Рис.31. Реальное представление интегрирующего звена (конденсатора)
Апериодическое звено Подставив в уравнение (1.63) значения b0 = 0 и a0 = 0, получим уравнение состояния следующего вида: a1 y′(t) + a2 y(t) = b1 x(t)(1.75.) Передаточная функция звена может быть найдена с помощью преобразования по Лапласу и будет иметь вид:
В данном случае Т = a1 /a2 – постоянная времени, характеризующая инерционность звена, k – передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к размерности входного. Постоянная времени – время, за которое величина выходного параметра принимает установившееся значение, т.е. с увеличением Т увеличивается инерционность звена. Звено называется апериодическим или инерционным звеном 1-го порядка, т.к. описывается дифференциальным уравнением первого порядка. При помощи обратного преобразования по Лапласу получим переходную функцию звена, при условии х(t) = 1(t):
Переходная функция апериодического звена является стабилизирующейся, т.к. при анализе переходной функции можно заметить, что значение величины выходного параметра при постоянном значении величины входного параметра, принимает установившееся значение через определенный промежуток времени. Для получения АФЧХ апериодического звена подставим в выражение (1.76.) jwвместор, и получим:
На основании данного выражения определим АЧХ апериодического звена:
и ФЧХ апериодического звена:
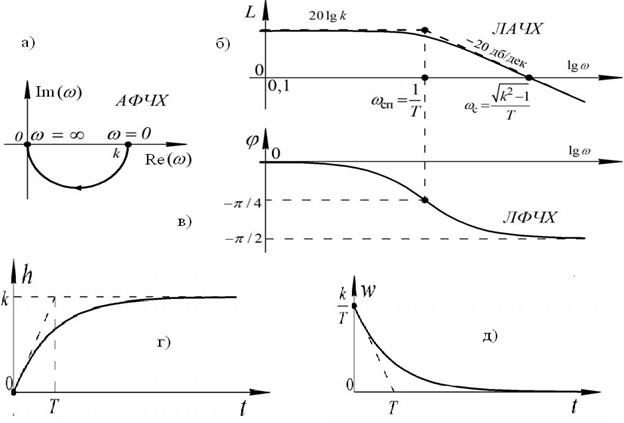
Графическое представление характеристик апериодического звена изображено на рисунке 32.
Рис.32. Характеристики апериодического звена: а), б), в) – частотные; г), д), - временные
Сплошной линией на рисунке 32,б показана кривая, точно соответствующая функции L(ω). На практике чаще всего используют приближенную характеристику данной функции, которая представляет собой ломаную, которая состоит из двух отрезков асимптот. Асимптотические функции являются кусочно-непрерывными функциями, они мало отличаются от действительной функции звена, и используются для упрощения расчетов. При представлении какой-либо функции с помощью асимптотической функции, ошибкой пренебрегают. Анализируя ЛАЧХ и ЛФЧХ (рисунок 32) нетрудно заметить, что амплитуда выходных колебаний не изменяется до достижения частоты входных колебаний ωсп, а с увеличением частоты входных колебаний ω > ωсп, амплитуда выходных колебаний начинает уменьшаться. На основании проведенного анализа можно сделать вывод, что апериодическое звено является фильтром высоких частот, потому что в основном передает на выход только низкие частоты. С увеличением частоты входных колебаний, их подавление возрастает и увеличивается их сдвиг по фазе. Сдвиг по фазе между входными и выходными колебаниями отрицательный и с увеличением частоты стремится к значению − π /2. Примерами апериодического звена могут служить: термопара, электродвигатель постоянного тока, четырехполюсник из сопротивления и т.д. Реальная реализация апериодического звена RC-цепочкой представлено на рисунке 33.
Рис.33. Апериодическое звено в виде RC-цепочки
Дифференцирующее звено Подставив в уравнение (1.63) значения b1 = 0 и a0 = a1 = 0, получим уравнение состояния следующего вида: a2 y(t) = b0 x′(t) (1.81.)
Уравнение идеального дифференцирующего звена будет иметь следующий вид:
В данном случае k – передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к скорости изменения величины входного параметра. Передаточная функция идеального дифференцирующего звена может быть найдена с помощью преобразования по Лапласу и будет иметь вид:
W(p) = kp (1.83.)
Переходная функция идеального дифференцирующего звена будет выражена:
h(t) = k δ(t) (1.84.)
Вышеуказанные функции являются нереализуемыми физически, потому что могут иметь бесконечные значения. На практике обычно применяют последовательное соединение дифференцирующего и апериодического звеньев, т.к. инерционное звено ограничивает усиление на высоких частотах и в диапазоне рабочих частот характеристики получившегося звена близки к требуемым. Для получения АФЧХ идеального дифференцирующего звена подставим в выражение (1.83.) jwвместо р, и получим:
W(jω) = jkω(1.85.) основании данного выражения определим АЧХ идеального дифференцирующего звена:
A(ω) = kω(1.86.)
и ФЧХ идеального дифференцирующего звена:
j(w ) = arctg(¥) = π/2 (1.87.)
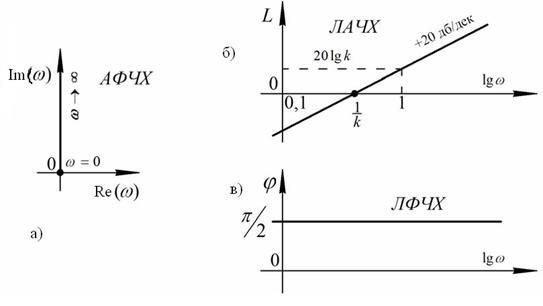
Графическое представление частотных характеристик идеального дифференцирующего звена изображено на рисунке 34.
Рис.34. Графическое представление частотных характеристик идеального дифференцирующего звена
Анализируя графики можно увидеть, что амплитуда выходных колебаний постоянно растет с ростом частоты входных колебаний. Сдвиг по фазе является постоянным, значение его равно π/2. Реализуемое на практике звено, получающееся из соединения идеального дифференцирующего и апериодического звеньев, называют дифференцирующим звеном с замедлением. Звено с замедлением используется для улучшения динамических характеристик систем автоматического управления. Передаточная функция такого звена описывается следующим выражением:
W(p) = kp /(Tp+1) (1.88.)
Временные характеристики дифференцирующего звена с замедлением и его реальное представление изображено на рисунке 35. При входной частоте колебанийω ® ¥ передаточный коэффициент звена стремится к k/T. Сдвиги по фазе между входными и выходными параметрами колебаний принимают наибольшее значение при низких частотах. При высокой частоте входных колебаний сдвиг по фазе стремится к нулю.
Рис.35 Временные характеристики и варианты реального представления дифференцирующего звена с замедлением
Колебательное звено . Подставив в уравнение (1.63.) значение b0 = 0, получим дифференциальное уравнение второго порядка (уравнение состояния) следующего вида:
a0 y′′( t) + a1 y′ (t) + a2 y (t) = b1 x (t)(1.89.)
Передаточная функция звена 2 порядка может быть найдена с помощью преобразования по Лапласу и будет иметь следующий вид:
где k = b0/a0 – передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к размерности входного в статическом режиме,
Так как pявляется комплексным числом, корни данного уравнения могут быть вещественными, мнимыми и комплексно-сопряженными. Для общего случая корни будут выглядеть, как:
где 0 < x < 1, в этом случае, переходная функция имеет затухающий характер. Передаточная функция колебательного звена в этом случае будет выглядеть:
Переходную функцию получим, применив обратное преобразование Лапласа:
при этом Графики временных характеристик колебательного звена представлены на рисунке 36.
Рис.36. Графики временных характеристик колебательного звена
При x = 0 колебательное звено называется консервативным, оно характеризуется незатухающими колебаниями на выходе. Консервативное звено представляет собой идеализированный генератор гармонических сигналов, работающий без потерь энергии. Передаточная функция консервативного звена будет иметь вид:
При x ≥ 1 колебательное звено представляет собой апериодическое звено 2 порядка. Апериодическое звено 2 порядка можно рассматривать, как последовательное соединение апериодических звеньев 1 порядка, о которых упоминалось выше. АФЧХ колебательного звена выражается в виде:
Действительная частотная характеристика звена Re(w) будет определяться первым слагаемым данного выражения, мнимая частотная характеристика Im(w) – вторым. Графическое представление частотных характеристик колебательного звена представлено на рисунке 37. Величина ωсп определяется, как точка пересечения асимптот, и ее численное значение равно ωсп = 1/ T.
Рис.37. Графики частотных характеристик колебательного звена
Анализируя ЛАЧХ И ЛФЧХ, можно заметить, что при увеличении частоты входных колебаний до частоты ωсп, амплитуда выходных колебаний постоянна, а при увеличении частоты входных колебаний более ωсп, амплитуда выходных колебаний начинает уменьшаться. Следовательно, колебательное звено фильтрует высокие частоты. Сдвиг по фазе между входными и выходными параметрами колебаний отрицателен и с увеличением частоты стремится к значению –π. С помощью степени затухания Ψ оценивают скорость затухания колебательного процесса, степень затухания представляют как:
где А1и А2– соседние амплитуды. Следовательно, чем ближе Ψ к единице, тем быстрее затухает колебательный процесс, а чем Ψ ближе к нулю, тем затухание колебательного процесса происходит медленнее. Величина Ψ зависит от соотношения вещественной α и мнимой β частей комплексных корней характеристического уравнения, поэтому может быть представлена в виде:
Степенью колебательности называют отношение мнимой части комплексного корня к вещественной части, выраженное как:
μ = β /α (1.96.3.) с учетом этого (1.96.2.) примет вид:
Ψ =1−e−2π /μ (1.96.4.)
Коэффициент демпфирования (затухания) ξ связан со степенью колебательности μ следующим соотношением:
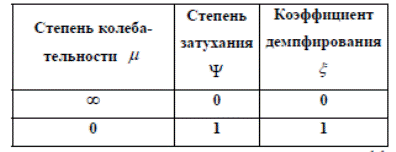
На рисунке 37.1 приведена таблица, в которой указана взаимосвязь между коэффициентами μ, Ψ и ξ .
Рис.37.1. Таблица взаимосвязи коэффициентов μ, Ψ и ξ При анализе таблицы легко обнаруживается, что степень колебательности противоположна степени затухания и коэффициенту демпфирования (затухания). Чем больше μ, тем меньше Ψ и ξ, и наоборот. Реализуемое на практике колебательное звено может представлять собой электрический колебательный контур с активным сопротивлением, изображенный на рисунке 38.
Рис.38. Реальное представление колебательного звена.
Запаздывающее звено Уравнение запаздывающего звена представляется в следующем виде:
y(t) = x(t - τ) (1.97.)
где τ- является временем запаздывания. При нулевых начальных условиях это уравнение принимает в операторной форме следующий вид:
Y (р) = X (р)℮-pt (1.98.)
Передаточная функция запаздывающего звена будет выглядеть, как:
W(p)= ℮-pt (1.99.)
АФЧХ запаздывающего звена выражается в виде:
W(jω) = Re(ω) + Im(ω) = A(ω)℮ jj(w)= cos ωτ - j sin ωτ (1.100.)
на основании данного выражения определим АЧХ и ФЧХ запаздывающего звена:
A(ω) = 1; j(w ) = arctg( - sin ωτ/ cos ωτ) = - ωτ(1.101.)
Переходная функция запаздывающего звена представлена в виде:
h(t) = 1(t − τ)(1.102.)
Импульсная переходная характеристика имеет следующее значение:
w(t) = h′(t) = δ (t −τ )(1.103.)
Графическое представление частотных характеристик запаздывающего звена представлено на рисунке 39.
Рис.39. Графики частотных характеристик запаздывающего звена
Анализируя графики частотных характеристик можно отметить, что выходной сигнал отстает по фазе от входного, и отставание увеличивается с увеличением частоты. В то же время соотношение амплитуд сигналов от частоты не зависит.
Рис.40. Графики временных характеристик запаздывающего звена
На практике запаздывающее звено ухудшает устойчивость реализуемой системы, при включении в систему данного звена ухудшается ее управляемость. Анализ и синтез таких систем затруднителен, поэтому на практике передаточную функцию запаздывающего звена заменяют при расчетах дробно-рациональными функциями.
|
|




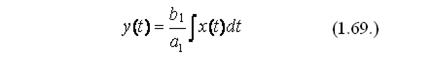



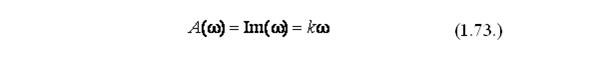











 - постоянная (времени) инерционности звена, с ее увеличением возрастает время изменения величины выходного параметра, при изменении входного.
- постоянная (времени) инерционности звена, с ее увеличением возрастает время изменения величины выходного параметра, при изменении входного.  - коэффициент демпфирования (затухания), чем он больше, тем быстрее затухают колебания. Корни уравнения знаменателя из выражения (1.90.) характеризуют переходной процесс звена, приравняем уравнение к нулю:
- коэффициент демпфирования (затухания), чем он больше, тем быстрее затухают колебания. Корни уравнения знаменателя из выражения (1.90.) характеризуют переходной процесс звена, приравняем уравнение к нулю:

 является постоянной времени затухания,
является постоянной времени затухания,  - собственная частота колебаний. Значением коэффициента x определяются динамические характеристики колебательного звена. Звено является колебательным только при
- собственная частота колебаний. Значением коэффициента x определяются динамические характеристики колебательного звена. Звено является колебательным только при
 (1.94.)
(1.94.) параметр начальной фазы переходного процесса.
параметр начальной фазы переходного процесса.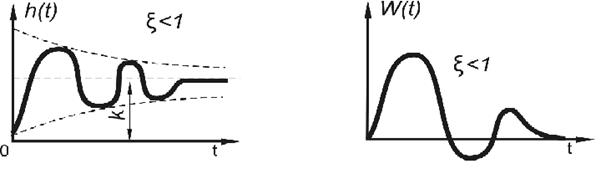
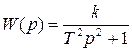 (1.95.)
(1.95.) (1.96.)
(1.96.)