|
|
Электромагнитные колебания. Переменный ток.Общие методические указания
При решении и оформлении задач необходимо соблюдать следующие требования: 1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины. 2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график. 3. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. Произвести вычисления по расчетной формуле с соблюдением правил приближенных вычислений. Результаты контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и дифференцированных зачетов.
Электростатика Основные формулы и законы · Закон Кулона
где · Напряженность и потенциал электростатического поля
где · Напряженность и потенциал электростатического поля, создаваемого точечным зарядом
· Поток вектора напряженности через площадку
где · Поток вектора напряженности через произвольную поверхность
· Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции (наложения) электростатических полей)
где · Связь между напряженностью и потенциалом электростатического поля
где · В случае поля, обладающего центральной или осевой симметрией,
· Для однородного поля (поля плоского конденсатора)
где · Электрический момент диполя (дипольный момент)
где · Линейная, поверхностная и объемная плотность зарядов, т.е. заряд, приходящийся соответственно на единицу длины, площади и объема:
· Теорема Гаусса для электростатического поля в вакууме
где · Напряженность поля, создаваемая равномерно заряженной бесконечной плоскостью,
· Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом
· Напряженность поля, создаваемого равномерно заряженной бесконечной цилиндрической поверхностью радиусом
· Работа, совершаемая силами электростатического поля при перемещении заряда
где · Вектор поляризации диэлектрика
где · Связь между вектором поляризации и напряженностью электростатического поля в той же точке внутри диэлектрика
где æ – диэлектрическая восприимчивость вещества. · Связь диэлектрической проницаемости e = 1 + æ. · Связь между напряженностью
· Связь между векторами электрического смещения и напряженности электростатического поля
· Связь между векторами
· Теорема Гаусса для электростатического поля в диэлектрике
где · Электроемкость уединенного проводника и конденсатора
где · Электроемкость плоского конденсатора
где · Электроемкость батареи конденсаторов: при последовательном (а) и параллельном (б) соединениях а) где
· Энергия уединенного заряженного проводника
· Потенциальная энергия системы точечных зарядов
где · Энергия заряженного конденсатора
где · Сила притяжения между двумя разноименно заряженными обкладками плоского конденсатора
· Энергия электростатического поля плоского конденсатора
где · Объемная плотность энергии электростатического поля
где Задания 1.1.Сила гравитационного притяжения двух водяных одинаково заряженных капель радиусами 0,1 мм уравновешивается кулоновской силой отталкивания. Определите заряд капель. Плотность воды равна 1 г/см3. [0,36 аКл]. 1.2.Во сколько раз сила гравитационного взаимодействия между двумя протонами меньше силы их кулоновского отталкивания? Заряд протона численно равен заряду электрона. [в 1,25∙1038 раза]. 1.3.Три одинаковых точечных заряда q1 =q2 = q3 = 2 нКл находятся в вершинах равностороннего треугольника со сторонами 10 см. Определите модуль и направление силы, действующей на один из зарядов со стороны двух других. [6,2мкН]. 1.4.В вершинах равностороннего треугольника находятся одинаковые положительные заряды q = 2 нКл. Какой отрицательный заряд q1 необходимо поместить в центр треугольника, чтобы сила притяжения со стороны заряда q1 уравновесила силы отталкивания положительных зарядов? [1,15нКл]. 1.5.Четыре одинаковых точечных заряда q1 =q2 = q3 = q4 = 2 нКл находятся в вершинах квадрата со стороной 10 см. Определите силу, действующую на один из зарядов со стороны трех других. [7мкН]. 1.6.Два шарика одинакового радиуса и массы подвешены на двух нитях так, что их поверхности соприкасаются. После сообщения шарикам заряда 4.10-7Кл они оттолкнулись друг от друга и разошлись на угол 60˚. Найдите массу каждого шарика, если длина нити 20 см. [1,56.10-3 кг]. 1.7.Два шарика массой 1 кг каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити 10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол 60˚? [7,6 мкКл]. 1.8.К бесконечно заряженной плоскости с поверхностной плотностью заряда 8,85 нКл/см2 прикреплен на нити одноименно заряженный шарик с массой 1г и зарядом 2нКл. Какой угол с плоскостью образует нить, на которой висит шарик?[45˚]. 1.9.С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости? Поверхностная плотность заряда на каждой плоскости 2 мкКл/м2? [0,2 Н/м2]. 1.10.С какой силой, приходящейся на единицу длины, отталкиваются две одноименно заряженные бесконечно длинные нити с одинаковой линейной плотностью заряда 2 мкКл/м, находящихся на расстоянии 2 см друг от друга? [3,6 Н/м]. 1.11.С какой силой электрическое поле заряженной бесконечной плоскости действует на каждый метр заряженной бесконечно длинной нити, помещенной в это поле? Поверхностная плотность заряда на плоскости равна 2 мкКл/м2 и линейная плотность заряда на плоскости 2 мкКл/м. [0,2Н/м]. 1.12.Тонкий прямой стержень длиной 15 см равномерно заряжен с линейной плотностью 0,10 мКл/м. На продолжении оси стержня на расстоянии 10 см от ближайшего конца находится точечный заряд 10 нКл. Определите силу взаимодействия стержня и заряда. [56 мН]. 1.13.На тонком стержне длиной 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня, на расстоянии 10 см от ближнего конца, находится точечный заряд 40 нКл, который взаимодействует со стержнем с силой 6 мкН. Определите линейную плотность заряда на стержне. [2,5 нКл/м]. 1.14.Два точечных заряда q1 =4 нКл и q2=-2 нКл находятся друг от друга на расстоянии 60 см. Определите напряженность поля в точке, расположенной посередине между зарядами. [0,6 кВ/м]. 1.15.Чему равна напряженность поля в точке, расположенной посередине между точечными зарядами q1 = 4нКл и q2= 2 нКл? Расстояние между зарядами равно 60 см. [0,2 кВ/м]. 1.16.Определите напряженность поля в точке, находящейся на прямой, соединяющей заряды q1 =10 нКл и q2=-8 нКл, на расстоянии 8 см справа от отрицательного заряда. Расстояние между зарядами равно 20 см. [10 кВ/м]. 1.17.Определите напряженность поля в точке, находящейся на прямой, соединяющей заряды q1 =10 нКл и q2=-8 нКл, на расстоянии 8 см слева от отрицательного заряда. Расстояние между зарядами равно 20 см. [17,5 кВ/м]. 1.18.Расстояние между двумя точечными зарядами 1.19.Расстояние между одноименными одинаковыми зарядами q = 2 нКл равно 10 см. Определите напряженность поля, создаваемого этими зарядами в точке, находящейся на расстоянии 8 см от первого и 6 см от второго заряда. [5,7 кВ/м]. 1.20.В вершинах квадрата со стороной 5 см находятся одинаковые положительные заряды q = 2 нКл. Определите напряженность электростатического поля: 1) в центре квадрата; 1.21.Электростатическое поле создается двумя бесконечными параллельными плоскостями, заряженными равномерно одноименными зарядами с поверхностной плотностью соответственно s1=2нКл/м2 и s2=4 нКл/м2. Определите модуль напряженности электростатического поля: 1) между плоскостями; 1.22.Электростатическое поле создается двумя бесконечными параллельными плоскостями, заряженными равномерно разноименными зарядами с поверхностной плотностью 1.23.На металлической сфере радиусом 15 см находится заряд q = 2 нКл. Определите напряженность электростатического поля: 1) на расстоянии 10 см от центра сферы; 2) на поверхности сферы; 3) на расстоянии 20 см от центра сферы. Постройте график зависимости напряженности поля от расстояния. [1) 0; 2) 800 В/м; 1.24.Кольцо радиусом 5 см из тонкой проволоки равномерно заряжено с линейной плотностью t = 14 нКл/м. Определите напряженность поля на оси, проходящей через центр кольца, в точке, удаленной на расстояние 10 см от центра кольца. [2,83 кВ/м]. 1.25.Поле создано двумя равномерно заряженными концентрическими сферами радиусами R1= 5 см и R2 = 8 см. Заряды сфер соответственно равны q1 = 2 нКл и q2 = -1 нКл. Определите напряженность электростатического поля в точках, лежащих от центра сфер на расстояниях: 1) r1 = 3 см; 2) r2 = 6 см; 3) r3 = 10 см. [1) 0; 2) 5 кВ/м; 3) 0,9 кВ/м]. 1.26.Определите поток ФЕ вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды q1 = 5 нКл и q2 = -2 нКл. [339 В×м]. 1.27.Определите поток ФЕ вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды q1 = 5 нКл и q2 = 2 нКл. [790 В×м]. 1.28.На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью 0,1 нКл/см2 расположена круглая пластинка. Нормаль к плоскости пластинки составляет с линиями напряженности угол 30°. Определите поток ФЕ вектора напряженности через эту пластинку, если ее радиус равен 15 см. [3,46 кВ×м]. 1.29.Электростатическое поле создается положительным точечным зарядом. Определите числовое значение и направление градиента потенциала этого поля, если на расстоянии 10 см от заряда потенциал равен 100 В. [1 кВ/м, направлен к заряду]. 1.30.Электростатическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью 5нКл/м2. Определите числовое значение и направление градиента потенциала этого поля. [282 В/м, направлен к плоскости]. 1.31.Электростатическое поле создается бесконечной прямой нитью, заряженной равномерно с линейной плотностью 50 пКл/см. Определите числовое значение и направление градиента потенциала в точке на расстоянии 0,5 м от нити. [180 В/м, направлен к нити]. 1.32.Расстояние между двумя точечными зарядами q1 = 2 нКл и q2 = -3 нКл, расположенными в вакууме, равно 20 см. Определите потенциал поля, создаваемого этими зарядами в точке, удаленной от первого заряда на расстояние 15 см и от второго заряда на 10 см. [–150В]. 1.33.Электростатическое поле создается в вакууме бесконечным цилиндром радиусом 8 мм, равномерно заряженным с линейной плотностью 10 нКл/м. Определите разность потенциалов между двумя точками этого поля, расположенными на расстояниях 2 мм и 7 мм от поверхности этого цилиндра. [73 В]. 1.34.Металлический шар радиусом 5 см имеет заряд 1.35.Тонкое кольцо радиусом 5 см из тонкой проволоки имеет равномерно распределенный заряд q = 10 нКл. Определите потенциал j электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр кольца, в точке, удаленной на расстояние 10 см от центра кольца. [1) 1,8 кВ; 2) 805 В]. 1.36.Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью s = 1 нКл/м2. Определите разность потенциалов между двумя точками этого поля, расположенными на расстоянии 20 и 50 см от плоскости. [16,9 В]. 1.37.Электростатическое поле создается равномерно заряженной сферической поверхностью радиусом 10 см с зарядом q=15нКл. Определите разность потенциалов между двумя точками этого поля, расположенными на расстоянии 5 см и 15 см от поверхности сферы. [360 В]. 1.38.Электростатическое поле создается сферой радиусом 5 см, равномерно заряженной с поверхностной плотностью 1.39.Электростатическое поле создается равномерно заряженным шаром радиусом 1 м и зарядом 50 нКл. Определите разность потенциалов для точек, расположенных от центра шара на расстоянии 1,5 и 2 м. [75 В]. 1.40.Электростатическое поле создается шаром радиусом 1.41.Электростатическое поле создается в вакууме непроводящим шаром радиусом 10 см, равномерно заряженным с объемной плотностью 20 нКл/м3. Определите разность потенциалов между точками, расположенными внутри шара на расстоянии 1.42.Электростатическое поле создается положительно заряженной с постоянной поверхностной плотностью 10 нКл/м2 бесконечной плоскостью. Какую работу надо совершить для того, чтобы перенести электрон вдоль линии напряженности с расстояния 2 см до 1 см от плоскости? [9,04.10-19 Дж]. 1.43.Под действием электростатического поля равномерно заряженной бесконечной плоскости точечный заряд q=1 нКл переместился вдоль силовой линии на расстояние 1 см; при этом совершена работа 5 мкДж. Определите поверхностную плотность заряда на плоскости. [8,85 мкКл/м2]. 1.44.Электростатическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью заряда 1 нКл/см. Какую скорость приобретет электрон, приблизившись к нити вдоль линии напряженности с расстояния 1,5 см до 1 см от нити? Начальная скорость электрона равна нулю. [16 Мм/с]. 1.45.Одинаковые заряды q = 100 нКл расположены в вершинах квадрата со стороной 10 см. Определите потенциальную энергию этой системы. [4,87 мДж]. 1.46.Сферическая поверхность имеет равномерно распределенный заряд. Определите радиус поверхности сферы, если потенциал в центре шара равен 200 В, а в точке, лежащей от его центра на расстоянии 50 см, 40 В. [10 см]. 1.47.Определите линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда q =1 нКл с расстояния 5 см до 2 см в направлении, перпендикулярном нити, равна 50 мкДж. [3,03 мКл/м]. 1.48.Электростатическое поле создается положительно заряженной бесконечной нитью. Протон, двигаясь от нити под действием поля вдоль линии напряженности с расстояния 1 см до расстояния5 см, изменил свою скорость от 1 до 10 Мм/с. Определите линейную плотность заряда нити. [17,8 мкКл/м]. 1.49.Определите ускоряющую разность потенциалов, которую должен пройти в электрическом поле электрон, чтобы его скорость возросла от 1Мм/с до 5 Мм/с. [68,3 В]. 1.50.Какую ускоряющую разность потенциалов должен пройти в электрическом поле электрон, чтобы получить скорость 8 Мм/с? [182 В]. 1.51.Определите ускоряющую разность потенциалов, которую должен пройти в электрическом поле электрон, обладающий скоростью 1 Мм/с, чтобы скорость его возросла в 2 раза. [8,5 В]. 1.52.Определите поверхностную плотность зарядов на пластинах плоского слюдяного (e=7) конденсатора, заряженного до разности потенциалов 200 В, если расстояние между его пластинами равно 0,5мм. [24,8 мкКл/м2]. 1.53.Расстояние между пластинами плоского конденсатора 5 мм. После зарядки конденсатора до разности потенциалов 500 В между пластинами конденсатора поместили стеклянную пластинку (e=7), полностью заполняющую пространство конденсатора. Определите: 1) диэлектрическую восприимчивость стекла; 2) поверхностную плотность связанных зарядов на стеклянной пластинке. [1) 6; 2) 759 нКл/м2]. 1.54.Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика — слюдяной пластиной (e1=7) толщиной d1 = 1 мм и парафиновой пластиной (e2=2) толщиной d2 = 0,5 мм. Определите: 1) напряженности электростатических полей в слоях диэлектрика; 2) электрическое смещение, если разность потенциалов между пластинами конденсатора U = 500 В. [1) Е1= 182 кВ/м, Е2 = 637 кВ/м; 2) D = 11,3 мкКл/м2]. 1.55.Расстояние между пластинами плоского конденсатора d = 5 мм, разность потенциалов U = 1,2 кВ. Определите: 1) поверхностную плотность заряда на пластинах конденсатора; 2) поверхностную плотность связанных зарядов на диэлектрике, если известно, что диэлектрическая восприимчивость диэлектрика, заполняющего пространство между пластинами, æ = 1. [1) 1.56.Пространство между пластинами плоского конденсатора заполнено стеклом (e = 7). Расстояние между пластинами 1.57.Определите расстояние между пластинами плоского конденсатора, если между ними приложена разность потенциалов U=150 В, причем площадь каждой пластины S=100 см2, ее заряд q=10 нКл. Диэлектриком является слюда (e =7). [9,29 мм]. 1.58.На пластинах плоского конденсатора находится заряд 10 нКл. Площадь каждой пластины конденсатора равна 100 см2 , диэлектрик – воздух. Определите силу, с которой притягиваются пластины. Поле между пластинами считать однородным. 1.59.Разность потенциалов между пластинами плоского конденсатора U=100 В. Площадь каждой пластины S=200 см2, расстояние между пластинами d=0,5 мм, пространство между ними заполнено парафином (e =2). Определите силу притяжения пластин друг к другу. [7,08 мН]. 1.60.Шар, погруженный в масло (e = 2,2), имеет поверхностную плотность заряда s=1 мкКл/м2 и потенциал j=500 В. Определите: 1) радиус шара; 2) заряд шара; 3) электрическую емкость шара; 4) энергию шара. [1) 9,74 мм; 2) 1,19 нКл; 3) 2,38 пФ; 4) 0,3 мкДж]. 1.61.К пластинам плоского воздушного конденсатора приложена разность потенциалов U1 = 500 В. Площадь пластин 1.62.К пластинам плоского воздушного конденсатора приложена разность потенциалов U1 = 500 В. Площадь пластин 1.63.Плоский воздушный конденсатор электроемкостью 1.64.К пластинам плоского воздушного конденсатора приложено напряжение U1= 500 В. Площадь пластин S = 200 см2, расстояние между ними dl1 = 1,5 мм. Пластины раздвинули до расстояния d2 = 15 мм. Найдите энергии W1 и W2 конденсатора до и после раздвижения пластин, если источник тока перед раздвижением отключался. [W1 = 14,8 мкДж, W2 = 148 мкДж]. 1.65.К пластинам плоского воздушного конденсатора приложено напряжение U1= 500 В. Площадь пластин S = 200 см2, расстояние между ними d1 = 1,5 мм. Пластины раздвинули до расстояния d2 = 15 мм. Найдите энергии W1 и W2 конденсатора до и после раздвижения пластин, если источник тока перед раздвижением не отключался. [W1 = 14,8 мкДж, W2 = 1,48 мкДж]. 1.66.Расстояние между пластинами заряженного плоского конденсатора уменьшили в 2 раза. Во сколько раз изменилась энергия и плотность энергии поля, если конденсатор остался присоединеннымк источнику постоянного напряжения? [увеличилась в 2 раза, увеличилась в 4 раза]. 1.67.Электроемкость батареи, образованной двумя последовательно соединенными конденсаторами, равна 100 пФ, а заряд батареи 20 нКл. Определите электроемкость второго конденсатора, а также разности потенциалов на обкладках каждого конденсатора, если электроемкость первого конденсатора200 пФ. 1.68.К батарее с напряжением 300 В подключены два плоских конденсатора с электроемкостями 2 пФ и 3 пФ. Определите заряд и напряжение на пластинах конденсаторов при последовательном их соединении. [0,36 нКл; 0,36 нКл;180 В;120 В]. 1.69.К батарее с напряжением 300 В подключены два плоских конденсатора с электроемкостями 2 пФ и 3 пФ. Определите заряд и напряжение на пластинах конденсаторов при параллельном их соединении. [0,6 нКл; 0,9 нКл; 300 В; 300 В]. 1.70.Конденсаторы с электроемкостями 2мкФ, 5 мкФ и
Основные формулы и законы
где
где
где
а) где
для однородного участка цепи
для неоднородного участка цепи
для замкнутой цепи
где
где
· Закон Джоуля-Ленца (количество теплоты, выделяемой при прохождении тока через проводник)
|
|
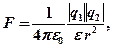
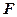 – модуль силы взаимодействия двух точечных зарядов
– модуль силы взаимодействия двух точечных зарядов  и
и  ;
;  – расстояние между зарядами;
– расстояние между зарядами;  - электрическая постоянная,
- электрическая постоянная,  -диэлектрическая проницаемость среды, в которой находятся заряды (для вакуума
-диэлектрическая проницаемость среды, в которой находятся заряды (для вакуума  )
) ;
;  , или
, или  ,
, – сила, действующая на точечный положительный заряд
– сила, действующая на точечный положительный заряд  , помещенный в данную точку поля;
, помещенный в данную точку поля;  – потенциальная энергия заряда
– потенциальная энергия заряда  – работа по перемещению заряда
– работа по перемещению заряда  на расстоянии
на расстоянии  ;
;  .
.
 ,
, – вектор, модуль которого равен
– вектор, модуль которого равен  к площадке;
к площадке;  – составляющая вектора
– составляющая вектора  по направлению нормали
по направлению нормали 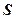
 .
.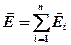 ;
;  ,
, ,
,  – соответственно напряженность и потенциал поля, создаваемого зарядом
– соответственно напряженность и потенциал поля, создаваемого зарядом  ,
,  – число зарядов, создающих поле.
– число зарядов, создающих поле. , или
, или  ,
, ,
,  ,
,  – единичные векторы координатных осей.
– единичные векторы координатных осей. .
.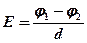 ,
, - разность потенциалов между пластинами конденсатора,
- разность потенциалов между пластинами конденсатора,  - расстояние между ними.
- расстояние между ними. ,
, – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному).
– плечо диполя (векторная величина, направленная от отрицательного заряда к положительному). ;
;  ;
; 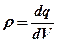 .
. ,
, – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности
– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности 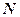 – число зарядов;
– число зарядов; 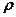 – объемная плотность зарядов.
– объемная плотность зарядов. .
. с зарядом
с зарядом  ;
; 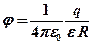 при
при  (внутри сферы);
(внутри сферы);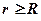 (вне сферы).
(вне сферы). при
при  из точки 1(потенциал
из точки 1(потенциал  ) в точку 2 (потенциал
) в точку 2 (потенциал  ),
), , или
, или  ,
, – проекция вектора
– проекция вектора  .
. ,
, – объем диэлектрика;
– объем диэлектрика; 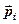 – дипольный момент
– дипольный момент  -й молекулы,
-й молекулы,  æe0
æe0  поля в диэлектрике и напряженностью
поля в диэлектрике и напряженностью  внешнего поля
внешнего поля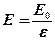 .
. .
.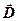 ,
, 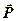
 .
. ,
, – составляющая вектора
– составляющая вектора  ;
;  – вектор, модуль которого равен
– вектор, модуль которого равен 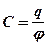 ,
, 
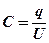 ,
, – потенциал проводника;
– потенциал проводника;  – разность потенциалов между пластинами конденсатора.
– разность потенциалов между пластинами конденсатора. ,
, , б)
, б)  ,
, – электроемкость
– электроемкость  .
. ,
, – потенциал, создаваемый в той точке, где находится заряд
– потенциал, создаваемый в той точке, где находится заряд  , всеми зарядами, кроме
, всеми зарядами, кроме  ,
, – его электроёмкость;
– его электроёмкость;  .
. ,
, – объем области между пластинами конденсатора.
– объем области между пластинами конденсатора. ,
,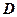 – электрическое смещение.
– электрическое смещение. 2. Постоянный электрический ток
2. Постоянный электрический ток Сила тока
Сила тока
 (если
(если  ).
). ,
,  ,
, – средняя скорость упорядоченного движения зарядов в проводнике,
– средняя скорость упорядоченного движения зарядов в проводнике,  – элементарный заряд.
– элементарный заряд. ,
, – длина проводника,
– длина проводника,  – удельное сопротивление,
– удельное сопротивление,  – удельная проводимость.
– удельная проводимость.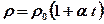 ,
, – температурный коэффициент сопротивления,
– температурный коэффициент сопротивления,  – удельное сопротивление при
– удельное сопротивление при  ,
,  – температура проводника.
– температура проводника. , б)
, б) 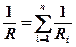 ,
, – сопротивление
– сопротивление  -го проводника,
-го проводника,  ) и напряжения (
) и напряжения (  ) в
) в  ,
, 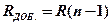 .
. ,
,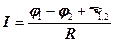 ,
, ,
, – разность потенциалов на концах участка цепи,
– разность потенциалов на концах участка цепи,  – ЭДС источника,
– ЭДС источника,  ,
, .
.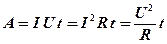 .
. .
.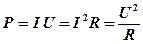 .
. Полная мощность, выделяемая в цепи,
Полная мощность, выделяемая в цепи,