|
|
Оптические свойства дисперсных систем.Реферат по Коллоидной химии г. Казань 2016 МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ СВОЙСТВА КОЛЛОИДНЫХ РАСТВОРОВ. ОСМОС. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
(1)
Где Sч – поверхность частицы, Vч – ее объем. К молекулярно- кинетическим свойствам дисперсных систем относятся: броуновское движение, осмос, диффузия. Диффузией называется процесс самопроизвольного выравнивания концентраций в системе, приводящий к установлению одинакового химического потенциала каждого компонента во всех элементах объема системы. Для описания диффузии используется первый закон Фика:
где – поток вещества, определяемый как количество вещества dm,
проходящего за время dt через поверхность S, D – коэффициент диффузии, grad C – градиент концентраций. Осмос- это самопроизвольное проникновение растворителя в раствор, отделенный от него полупроницаемой перегородкой. В дальнейшем этот поток уравновешивается возникающим встречным градиентом давления. Этот процесс обусловлен, в термодинамической трактовке, ростом энтропии системы, а в кинетической, - избыточным числом ударов молекул растворителя о мембрану со стороны более разбавленного раствора. Принципиально осмос в дисперсных системах и растворах высокомолекулярных соединений не отличается от осмоса растворов низкомолекулярных соединений.
где - частичная концентрация – это число частиц в единице объема,
, k – постоянная Больцмана.
Осмотическое давления золей очень малая величина. Это объясняется чрезвычайно малыми значениями частичной концентрации или, иными словами, чрезвычайно большими значениями частичного веса коллоидных частиц
Осмотическое давление не постоянная величина. Это объясняется явлением агрегации, характерным для дисперсных систем:
Совместное рассмотрение явления осмоса и диффузии приводит к выводу уравнения Эйнштейна:
где - константа Больцмана, B – коэффициент вязкого сопротивления среды.
Для сферических частиц:
(7) где η - вязкость среды, r – радиус частицы. Поэтому для сферических частиц коэффициент диффузии может быть вычислен по формуле:
Источником броуновского движения являются не внешние причины, а внутренние, присущие системе. Иными словами, движение обусловлено столкновениями молекул среды (жидкости или газа) со взвешенными в ней частицами. Броуновское движение частиц описывается уравнением Эйнштейна – Смолуховского:
где
Кроме поступательного, существует вращательное броуновское движение. В этом случае находится средний квадрат случайного поворота частицы вокруг оси
Где Θ - коэффициент вращательной диффузии. Для сферических частиц коэффициент вращательной диффузии определяют по формуле:
Некоторые свойства растворов обусловлены не их химическим составом, а только числом частиц, участвующих в тепловом движении. Среди этих свойств — диффузия, осмотическое давление, понижение давления пара над раствором, изменение температур кипения и замерзания. Эти свойства называют молекулярно-кинетическими, или коллигативными (от colligate — обобщать). На заре развития коллоидной химии считалось, что коллоидным растворам не присущи молекулярно-кинетические свойства. Отсутствие диффузии и осмоса одно время и вовсе рассматривали как отличительный признак коллоидных растворов. Однако использование более точных методов исследования показало, что это не совсем так. Немецкий физикохимик Вольфганг Оствальд в связи с этим назвал дисперсные системы «миром обойденных величин». В свободнодисперсных системах также происходит движение частиц, но из-за больших (по сравнению с молекулами) размеров они двигаются значительно медленнее; связанные с их движением свойства менее выражены. По этой же причине замедлено движение молекул в растворах ВМС, их молекулярно-кинетические свойства аналогичны свойствам дисперсных систем с жидкой дисперсионной средой. Еще в 1827 году английский ботаник Р. Броун обнаружил, что частицы цветочной пыльцы, распределенные в воде, непрерывно двигаются по сложным беспорядочным траекториям (броуновское движение). Основные положения теории броуновского движения и его макроскопического проявления - диффузии - были разработаны А.Эйнштейном и М. Смолуховским в 1905 г. Эйнштейн вывел количественную теорию броуновского движения, однако он сомневался, что опыты такой точности можно осуществить. Теория Эйнштейна получила блестящие экспериментальные доказательства сначала в опытах Зеддига, подтверждающих зависимость среднеквадратичного сдвига от температуры (1908 г.), затем в экспериментах Т. Сведберга по измерению среднего сдвига в золях золота в зависимости от времени и вязкости среды (1909 г.). В 1908–1913 годах французский физик Ж.Б.Перрен занимался экспериментальным исследованием броуновского движения, вначале даже не зная о работе Эйнштейна в этой области. Перрен использовал измеренный им с помощью ультрамикроскопа среднеквадратичный сдвиг коллоидных частиц гуммигута в воде, открыл диффузионно-седиментационное равновесие (закон Лапраса-Перрена, или гипосометрический / барометрический закон) и на основании этих исследований определил значение числа Авогадро. Эти знаменитые опыты послужили подтверждением существования молекул. В 1926 году Ж. Б. Перрен получил Нобелевскую премию по физике «за работу по дискретной природе материи и, в особенности, за открытие седиментационного равновесия». В 1923 шведский физик и химик Т. Сведберг разработал скоростную ультрацентрифугу, которая позволила разделять коллоидные частицы и определять их массы и молекулярные массы полимеров, тем самым реализовал идею по использованию центрифуги для исследования коллоидных систем, высказанную А.В. Думанским в 1907 г. За комплекс работ по изучению дисперсных систем и растворов полимеров Т. Сведберг в 1926 г. был удостоен Нобелевской премии по химии. Диффузией называется самопроизвольно протекающий процесс выравнивания концентрации коллоидных частиц в растворе под влиянием их теплового хаотического движения. Явление диффузии необратимо. Коэффициент диффузии численно равен количеству вещества, продиффундировавшего через единицу площади в единицу времени при градиенте концентрации, равном 1 (т.е. изменению концентрации в 1 моль/см3 на расстоянии в 1 см). А. Эйнштейн (1906) вывел уравнение, связывающее коэффициент диффузии с абсолютной температурой, вязкостью и размером частиц дисперсной фазы:
где T - температура, К; r - радиус частицы, м; η - вязкость, Н•с/м2; кБ - постоянная Больцмана, 1,38•10-23; D - коэффициент диффузии, м2/с. Коэффициент диффузии прямо пропорционален температуре и обратно пропорционален вязкости среды (η) и радиусу частиц (r). Причиной диффузии, как и броуновского движения, является молекулярно-кинетическое движение частиц растворителя и вещества. Известно, что кинетическая энергия движущейся молекулы тем меньше, чем больше ее объем (табл. 13.2). Пользуясь уравнением Эйнштейна, можно легко определить массу 1 моля вещества, если известны D, T, η и r. Из уравнения (13.1) можно определить r:
где R - универсальная газовая постоянная, 8,3 (Дж/моль-К); Na постоянная Авогадро. Таблица 13.2.Коэффициент диффузии некоторых веществ
В случае когда система отделена от других частей системы перегородкой, которая проницаема для одного компонента (например, вода) и непроницаема для другого (например, растворенного вещества), диффузия становится односторонней (осмос). Сила, обусловливающая осмос, отнесенная к единице поверхности мембраны, называется осмотическим давлением. Роль полупроницаемых перегородок (мембран) могут выполнять ткани человека, животных и растений (мочевой пузырь, стенки кишечника, оболочки клеток и др.). Для коллоидных растворов осмотическое давление меньше, чем в истинных растворах. Процесс диффузии сопровождается возникновением разности потенциала в результате различной подвижности ионов и образования градиента концентрации (мембранного потенциала). Седиментация.На распределение частиц оказывает влияние не только диффузия, но и гравитационное поле. Кинетическая устойчивость коллоидной системы зависит от действия двух факторов, направленных взаимно противоположно: силы тяжести, под действием которой частицы оседают, и силы, при которой частицы стремятся разойтись по всему объему и противодействовать оседанию. Оптические свойства коллоидных растворов. Светорассеяние. Уравнение Д. Рэлея.Различить коллоидный и истинный растворы с первого взгляда невозможно. Хорошо приготовленный золь - практически чистая прозрачная жидкость. Микрогетерогенность его можно обнаружить специальными методами. Если золь, находящийся в неосвещенном месте, осветить узким лучом, то при наблюдении сбоку можно увидеть светлый конус, вершина которого находится в месте входа луча в негомогенное пространство. Это так называемый конус Тиндаля - своеобразное мутное свечение коллоидов, наблюдаемое при боковом освещении, называется эффектом Фарадея-Тиндаля. Причина этого характерного для коллоидов явления в том, что размер коллоидных частиц меньше половины длины световой волны, при этом наблюдается дифракция света, в результате рассеивания частицы светятся, превращаясь в самостоятельный источник света, и луч становится видимым. Теория рассеивания света разработана Рэлеем в 1871 году, который вывел для сферических частиц уравнение, связывающее интенсивность падающего света (I0) с интенсивностью света, рассеянного единицей объема системы (Ip).
где I, I0 - интенсивность рассеянного и падающего света, Вт/м2; кр - константа Рэлея, постоянная, зависящая от показателей преломления веществ дисперсной фазы и дисперсионной среды, м-3; сv - концентрация частиц золя, моль/л; λ - длина волны падающего света, м; r - радиус частицы, м. К молекулярно-кинетическим свойствам относятся: 1. Броуновское движение. 2. Диффузия. 3. Осмотическое давление. 4. Седиментация. Броуновское движение - это непрерывное беспорядочное движение частиц микроскопических и коллоидных размеров, не затухающее во времени. Это движение тем интенсивнее, чем выше температура и чем меньше масса частиц и вязкость дисперсионной среды. 1) В 1927г. английский ботаник Броун заметил, что частицы цветочной пыльцы, взвешенные в воде, находящиеся в поле зрения микроскопа, непрерывно двигаются по сложным траекториям, ни на мгновение не оставаясь в покое. Это движение пытались объяснить проявлением особенностей живой материи. Но, оказалось, что подобное непрерывное движение совершают и неорганические частицы. ( суспензии, суспензии неорганических веществ) Дальнейшее исследование показало, что отдельные частицы движутся совершенно независимо одна от другой; и движение происходит тем энергичнее, чем меньше их размеры. В результате огромного числа ударов, которые наносят молекулы среды коллоидной частице, последняя меняет свое направление и скорость весьма часто. За одну секунду коллоидная частица может изменить свое направление свыше В таких условиях определить истинный путь коллоидной частицы невозможно, но легко определить среднее расстояние, на которое она смещается в единицу времени. Для этого зарисуем следующую схему, где представлена проекция движения частицы на плоскость, при броуновском движении.
Количественной мерой перемещение частицы является величина среднего смещения (или сдвига) частицы Смещением или сдвигом частицы называют расстояние между проекциями начальной т.1и конечной т.2точек траектории на ось смещений (ось Х). Смещения одинаково вероятны как слева на право, так и в противоположном направлении. Поэтому при вычислении среднего смещения за большой промежуток времени
Где n – число смещений (число отрезков, ломанной линии), взятых для расчета
Эйнштейном и Смолуховским было показано, что среднее значение квадрата смещения частицы за время t равно
где R – универсальная газовая постоянная; T – абсолютная температура; 𝞰 – вязкость среды; r – радиус взвешенных частиц;
t – время. Из уравнения Эйнштейна–Смолуховского следует, что величина Диффузией – называют самопроизвольный процесс выравнивания концентрации частиц по всему объему раствора или газа под влиянием теплового (или броуновского) движения. Условия протекания диффузии: Направление процесса: Предел протекания: Процесс диффузии идет самопроизвольно, это явление необратимо, т.е. протекает до полного выравнивания концентраций. Перенос массы в результате диффузии сходен с закономерностями переноса тепла или электричества. Для диффузии характерно два режима течения: 1. Стационарный режим течения. 2. Нестационарный режим течения. Воспользовавшись такой аналогией ФИК (1855г.) сформулировал 1ый закон диффузии: Стационарная диффузия, когда grad(c) Где m – количество продиффундировавшего вещества; D – коэффициент диффузии, зависящий от свойств диффундирующих частиц и среды;
Знак « – »перед правой частью равенства поставлен потому, что производная Уравнение (1) можно представить также в виде:
Удельный или диффузионнный поток Где S – площадь поперечного сечения, через которую диффундируют вещество. – D – коэффициент диффузии. Если принять S, Он является в этом уравнении коэффициентом пропорциональности, физический смысл которого легко выяснить, перенеся в правую часть уравнения все члены кроме dm. Нестационарная диффузия, когда grad(c)= Эйнштейн вывел уравнение, связывающее коэффициент диффузии D c абсолютной температурой Т, вязкостью дисперсной среды Для вывода этого уравнения, имеющего большое практическое и теоретическое значение, представим трубку с сечением в S c Выделим мысленно в трубе слой раствора бесконечно малой величины, и ограниченный плоскостями: Х1Х1' и X2X2' объем этого слоя V будет равен Sdx. Обозначим концентрацию раствора и осмотическое давление слева от этого слоя через С1 и П1, а справа- С2 П2. Очевидно, Рассматривая диффузию в целом как направленный поток частиц, можно говорить о некоторой эффективной постоянной скорости частиц, (такой скоростью должны обладать все частицы, чтобы двигаясь прямолинейно, перенести через единицу сечения за единицу времени при данном градиенте концентрации определенного количества вещества) может быть объяснено тем, что движущая сила f, действующая на отдельную частицу, уравновешивается обратно направленной силой трения f= Сила трения Для сферических частиц коэффициент по Стоксу В=6 𝞰 – динамическая вязкость среды Для вычисления движущей силы, действующей на одну частицу, определим сначала движущую силу F, приходящуюся на единицу объема слоя: F= Тогда, если молярную концентрацию растворенного вещества обозначим через С, то движущую силу f, приходящуюся на одну частицу, можно представить: Где R– универсальная газовая постоянная Т– абсолютная температура Вставляя найденные выражения для Это уравнение можно переписать следующим образом: Но величина m = Согласно уравнению Фика для тех же условий : Приравнивая правые части уравнений 9 и 10 находим: D= В= D= Пользуясь уравнением Эйнштейна можно определить массу 1 моля вещества, если известны значения D,T, 𝞰. Из уравнения 12 следует: Определив по этому уравнению радиус частиц можно вычислить массу 1 моля вещества- М: М= Итак, мы рассмотрели с вами уравнение Эйнштейна, связывающее коэффициент диффузии D с температурой, вязкостью дисперсной среды 𝞰 и радиусом дисперсной фазы r. D= Причина диффузии дисперсной фазы в коллоидных системах является броуновское движение частиц. Если существует связь между броуновским движением и диффузией, то должна существовать связь между средним квадратичным значением проекции смещения частицы Эта связь была установлена Эйнштейном (1905) и Смолуховским (1906), независимо друг от друга Для установления зависимости И понятно, что за счет броуновского движения, перенос любой частицы вероятен и вправо и влево. Масса вещества, перенесенного за время t, через воображаемую плоскость MN вправо : влево: Очевидно, количество вещества продиффундировавшее через плоскость MN слева на право; выразится уравнением: Но из рисунка следует, что: Подставив уравнение 3 в уравнение 1 , получим: Объединив уравнение 4 и уравнение Фика: Имеем: Из этого следует важный вывод, что величина Диффузия проявляется в различных отраслях техники, в процессах жизнедеятельности. Она служит основой ряда распространенных технологий и операций: - дублении кожи; - выделки меха; - крашение ткани; - химико - техническая обработка металлов; - очистка газов с помощью диффузионных насосов и др. В пищевой промышленности диффузия имеет место при извлечении продукта из сырья. Например: коллоидный раствор, который образуется после извлечения сахарозы из клеток сахарной свеклы или другого растительного сырья, называют диффузионным соком. Седиментация. Седиментация (от лат. sedimentum — оседание), оседание или всплывание частиц дисперсной фазы (твёрдых крупинок, капелек жидкости, пузырьков газа) в жидкой или газообразной дисперсионной среде в гравитационном поле или поле центробежных сил. Седиментация происходит, если направленное движение частиц под действием силы тяжести или центробежной силы преобладает над хаотическим тепловым движением частиц (см. Броуновское движение, Диффузия). Скорость седиментации зависит от массы, размера и формы частиц, вязкости и плотности среды, а также ускорения, возникающего при действии на частицы сил поля. Для мелких не взаимодействующих между собой сферических частиц скорость седиментации определяется по Стокса формуле. Седиментация вдисперсных системах (особенно с газовой дисперсионной средой) часто сопровождается укрупнением седиментирующих частиц вследствие коагуляции или коалесценции. Седиментация в природе приводит к образованию осадочных горных пород, осветлению воды в водоёмах, освобождению атмосферы от находящихся в ней капельножидких и твёрдых частиц. В производственной практике седиментацию используют для разделения порошков на фракции, выделения в виде осадка различных продуктов химической технологии (См. также Отмучивание, Отстаивание, Седиментационный анализ.) Седиментационный анализ - один из наиболее широко применяемых непрямых методов определения размера частиц и их распределения по размерам. Седиментационный анализ основан на зависимости скорости осажденияоднородных частиц от их размеров. Грубодисперсные системы изучают методом седиментации в гравитационном поле, а тонкодисперсные и коллоидно-дисперсные - методом седиментации в центрифуге и в ультрацентрифуге. В вязкой и плотной среде при седиментации частица движется под действием силы тяжести в гравитационном поле. Сила сопротивления среды, действующая на сферическую частицу, зависит от ее размера, скорости движения,вязкости среды и характеризуется числом Рейнольдса где r – радиус частиц; U – скорость движения; r1,h – плотность и вязкость среды. Коэффициент сопротивления среды движущейся частицы где F – сила сопротивления среды. В соответствии с законом Стокса Гидродинамическое сопротивление среды описывается законом Ньютона-Риттера Сопротивление среды определяется суммой сил по уравнениям (2.2.11) и (2.2.12): В области чисел Рейнольдса (Re<<1) можно пренебречь вторым слагаемым уравнения (2.2.13), а при (Re>>1) – первым. В промежуточном случае можно использовать уравнение Озеена: Закон Стокса справедлив в области Re<<0,2. Поправка Озеена существенна в области чисел от 0,2 до 10, а закон Ньютона-Риттера описывает движение частиц в области чисел Рейнольдса от 102 до 105. Если размер частиц и скорость их осаждения невелики, то для описания силы сопротивления среды можно использовать закон Стокса. Сила тяжести, действующая на частицу, равна кажущейся массе, где g – ускорение свободного падения. Движение частиц будет направлено вниз, если разность плотностей дисперсной фазы r2 и дисперсионной среды r1(Dr) положительна, и частицы будут всплывать при Dr<0. Под действием силы Р частицы приходят в равномерно ускоренное движение. Но так как, кроме силы тяжести, на них действует сила сопротивления среды, направленная противоположно и возрастающая пропорционально скорости, то очень скоро сила сопротивления среды уравновешивает силу тяжести, благодаря этому далее движение идет равномерно со скоростью U. Если экспериментально определить скорость седиментации, то можно рассчитать радиус частиц; так как при стационарном режиме осаждения F = P. Поэтому откуда следовательно Уравнение Стокса (2.2.17) было выведено при соблюдении ряда условий, которые не всегда соблюдаются в реальных системах: 1. Частицы должны быть сферическими. Это условие обычно выполняется для разбавленных эмульсий и частиц полимеров, полученных методом эмульсионной полимеризации. Частицы суспензий часто отклоняются от сферической формы, поэтому для них определяется некоторый эффективный радиус частицы той же массы, движущейся с той же скоростью. Такой радиус называют эквивалентным или эффективным. 2. Отсутствие взаимодействия между частицами. Расстояние между частицами должно быть достаточно большим, чтобы падение одних частиц не сказывалось на скорости других. Поэтому анализ следует проводить при невысокихконцентрациях (1-2%). 3. Необходимо, чтобы сосуд, в котором происходит седиментация, был намного больше размеров частиц. Это необходимо для того, чтобы можно было пренебречь влиянием стенок, так как вблизи стенок скорость оседания не следует закону Стокса. 4. Движущиеся частицы должны быть твердыми и гладкими. Это условие связано с возможностью изменения формы частиц в результате возникновения в них микропотоков. Условие не выполняется при течении эмульсий. 5. Отсутствие проскальзывания между оседающей частицей и средой. Необходимо, чтобы частица хорошо смачивалась жидкостью, так как в уравнение (2.2.17) входит h – вязкость именно жидкости. 6. Скорость оседания должна быть постоянной, иначе сила тяжести не уравновесится силой трения. 7. Скорость оседания должна быть небольшой, в противном случае возникает турбулентный режим течения, и тогда нельзя будет использовать вязкость h, соответствующую ламинарному режиму течения.
Седиментационный анализ суспензий и эмульсий. В практике бурения скважин и их эксплуатации широко используют различные промывочные и цементные растворы, нефтяные эмульсии, пены и ряд других микрогетерогенных систем. Одной из наиболее важных характеристик таких систем является их полидисперсность, поэтому для теории и практики важно знать фракционный состав таких систем, то есть количественное распределение частиц по их размерам (радиусам). Несмотря на относительно малое содержание частиц с коллоидными размерами в указанных выше системах, их присутствие во многом определяет физико-механические и реологические свойства таких систем. Это объясняется тем, что на фракцию частиц с коллоидными размерами приходится большая часть общей межфазной поверхности. Учет и исследование этого фактора имеет большое значение при приготовлении и регулировании свойств дисперсных систем, применяемых в нефтепромысловом деле, а также при расчете и конструировании электродегидраторов, отстойных и очистных устройств. Знание распределения частиц породы по радиусам необходимо также для расчета запаса нефти в нефтяных коллекторах (определение свободного межпорового пространства). Одним из важнейших методов исследования полидисперсных систем является седиментационный анализ, дающий возможность находить так называемую “функцию распределения”, то есть определять содержание частиц в системе с заданными размерами (радиусами). Принцип седиментационного анализа состоит в измерении скорости оседания частиц дисперсной фазы в какой-либо дисперсионной среде. В основе седиментационного анализа лежит закон Стокса, по которому сила трения
Если частица движется под действием силы тяжести и размеры ее таковы, что она движется равномерно, то сила трения уравновешивает силу тяжести, действующую на частицу:
где D иd - плотность дисперсной фазы и дисперсионной среды, соответственно;g - ускорение силы тяжести (9,81м/c2). Из уравнения (2.17) получим:
|
|
 Молекулярно- кинетическая теория изучает законы самопроизвольного движения молекул. Некоторые свойства растворов обусловлены этим движением, т. е. Определяются не составом, а числом кинетических единиц- молекул в единице объема или массы. Коллоидно-дисперсные и микрогетерогенные системы обычно характеризуются дисперсностью, в качестве меры которой принята удельная поверхность. Удельная поверхность дисперсной фазы, содержащей одинаковые частицы, вычисляется по формуле:
Молекулярно- кинетическая теория изучает законы самопроизвольного движения молекул. Некоторые свойства растворов обусловлены этим движением, т. е. Определяются не составом, а числом кинетических единиц- молекул в единице объема или массы. Коллоидно-дисперсные и микрогетерогенные системы обычно характеризуются дисперсностью, в качестве меры которой принята удельная поверхность. Удельная поверхность дисперсной фазы, содержащей одинаковые частицы, вычисляется по формуле: (2)
(2)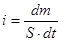
 (3)
(3)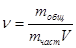
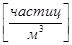
 по сравнению с молекулярным. Для двух систем при одной температуре:
по сравнению с молекулярным. Для двух систем при одной температуре: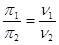 (4)
(4) (5)
(5)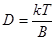 , (6)
, (6)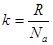
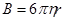
 , [
, [  ] (8)
] (8) (9)
(9) - средний квадрат смещения частицы вдоль любой оси за время t. Для расчета
- средний квадрат смещения частицы вдоль любой оси за время t. Для расчета  (10)
(10) , который также зависит от выбранных промежутков времени:
, который также зависит от выбранных промежутков времени: (11)
(11)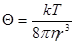 (12)
(12)



 раз.
раз.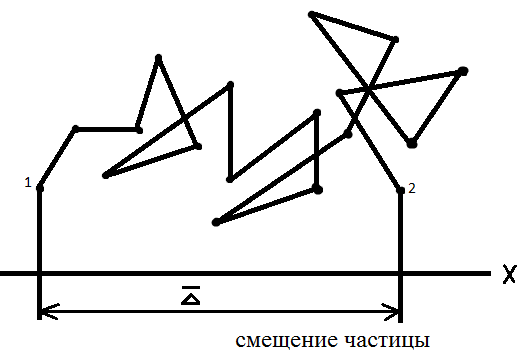
 за некоторый промежуток времени t.
за некоторый промежуток времени t. ,
, - отдельные проекции на ось Х.
- отдельные проекции на ось Х. ,
, – постоянная Авогадро;
– постоянная Авогадро;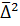 обратно пропорциональна радиусу частицы. Это означает, что чем крупнее частица, тем меньше величина ее смещения.
обратно пропорциональна радиусу частицы. Это означает, что чем крупнее частица, тем меньше величина ее смещения.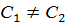

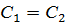

 , т.е.
, т.е.  ,
, 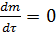 и подчиняется I закону Фика :
и подчиняется I закону Фика : 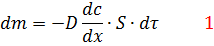
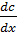 – градиент концентрации, который является движущей силой диффузии;
– градиент концентрации, который является движущей силой диффузии; – площадь, через которую идет диффузия;
– площадь, через которую идет диффузия; продолжительность диффузии.
продолжительность диффузии. 2
2 – количество вещества, проходящего через площадь сечения в 1
– количество вещества, проходящего через площадь сечения в 1  за 1 сек. и пропорционален градиенту концентрации (или это количество вещества, переносимое в результате диффузии за единицу времени через сечение, равное единице площади при
за 1 сек. и пропорционален градиенту концентрации (или это количество вещества, переносимое в результате диффузии за единицу времени через сечение, равное единице площади при  3
3 – изменение количества вещества, моль.
– изменение количества вещества, моль. – изменение времени,
– изменение времени, 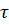 , сек.
, сек. градиент концентрации, знак «–» выражает уменьшение концентрации с расстоянием
градиент концентрации, знак «–» выражает уменьшение концентрации с расстоянием или dm= –DS
или dm= –DS 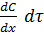



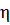 и радиусом частиц дисперсной фазы r.
и радиусом частиц дисперсной фазы r. , заполненного вещества равномерно убывает слева на право.
, заполненного вещества равномерно убывает слева на право.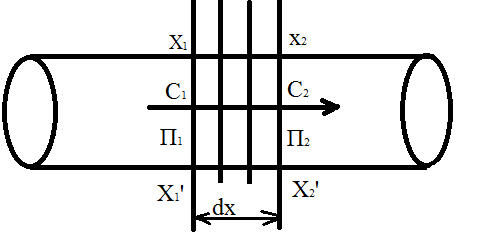
 и
и  ; при таких условиях в трубке происходит диффузия растворенного вещества, причем перенос вещества будет идти слева направо, как указ. На рис.
; при таких условиях в трубке происходит диффузия растворенного вещества, причем перенос вещества будет идти слева направо, как указ. На рис. , испытываемой этой частицей, т.е. что
, испытываемой этой частицей, т.е. что равна произведению коэффициента трения В между частицей и средой на скорость движения частицы ʋ:
равна произведению коэффициента трения В между частицей и средой на скорость движения частицы ʋ: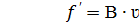 5
5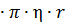

 6
6 в уравнение 4 получаем:
в уравнение 4 получаем: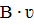 =
=  7
7 =
=  8
8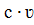 есть не что иное, как количество вещества m, продиффундировавшее в единицу времени через единицу площади. Поэтому
есть не что иное, как количество вещества m, продиффундировавшее в единицу времени через единицу площади. Поэтому 10
10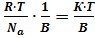 (11) уравнение Эйнштейна
(11) уравнение Эйнштейна для сферических частиц, тогда
для сферических частиц, тогда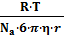 или D=
или D=  12
12 =
=  13
13 , где
, где  плотность дисперсной фазы, которая обычно известна.
плотность дисперсной фазы, которая обычно известна.
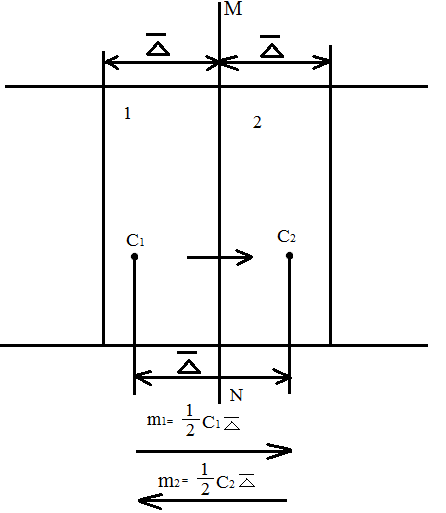
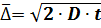 уравнение Эйнштейна – Смолуховского или
уравнение Эйнштейна – Смолуховского или  .
.
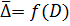 , представим себе трубку с поперечным сечением в S
, представим себе трубку с поперечным сечением в S  ; Пусть
; Пусть  среднее квадратичное значение проекции смещение частицы на ось, параллльную направлению диффузии, за время t.
среднее квадратичное значение проекции смещение частицы на ось, параллльную направлению диффузии, за время t.

 (1)
(1) (2) или
(2) или  3
3 (4)
(4)
 (5) или
(5) или  ( 6)
( 6) . Пользуясь данным уравнением по экспериментально определенному броуновскому движению, находят коэффициенты диффузии. Для истинных размеров коэффициенты диффузии D=
. Пользуясь данным уравнением по экспериментально определенному броуновскому движению, находят коэффициенты диффузии. Для истинных размеров коэффициенты диффузии D=  и для высокодисперсных систем D=
и для высокодисперсных систем D=  .
. , (2.2.9)
, (2.2.9) , (2.2.10)
, (2.2.10)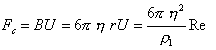 . (2.2.11)
. (2.2.11)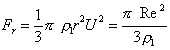 . (2.2.12)
. (2.2.12) . (2.2.13)
. (2.2.13) . (2.2.14)
. (2.2.14) , (2.2.15)
, (2.2.15) , (2.2.16)
, (2.2.16) или
или  , (2.2.17)
, (2.2.17) . (2.2.18)
. (2.2.18) , возникающая при движении шарообразной частицы радиусомr со скоростьюuв среде с вязкостьюh, выражается уравнением:
, возникающая при движении шарообразной частицы радиусомr со скоростьюuв среде с вязкостьюh, выражается уравнением: . (2.16)
. (2.16) . (2.17)
. (2.17) . (2.18)
. (2.18)