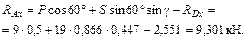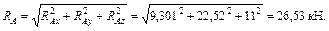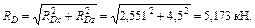|
|
Пример решения задачи типа С-5РАВНОВЕСИЕ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ Краткие сведения из теории Равновесие тела, на которое действует система Сходящихся в пространстве сил При рассмотрении равновесия тел, на которые действуют пространственные системы сил, необходимо составлять большее число уравнений равновесия, чем для случая плоских систем сил (см. п. 1.1.6). Если на тело действует система сходящихся сил в пространстве, то должны быть равны нулю алгебраические суммы проекций всех сил на три оси координат:
На рисунке 5.1 приведен пример, в котором вектор
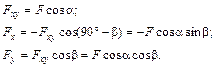
Равновесие тела под действием Произвольной пространственной системы сил Для равновесия тела, находящегося под действием произвольной пространственной системы сил, необходимо и достаточно, чтобы были равны нулю алгебраические суммы проекций всех сил на оси координат и суммы моментов всех сил относительно этих осей:
Чтобы найти момент силы относительно оси, следует спроецировать эту силу на плоскость, перпендикулярную оси, а затем определить момент полученной проекции относительно точки пересечения оси с названной плоскостью.
Если вектор силы лежит в одной плоскости с осью, то момент силы относительно оси равен нулю. На рисунке 5.2 приведен пример нахождения момента силы
Прежде чем перейти к разбору решения задачи, уточним некоторые моменты, касающиеся расстановки сил реакций связей.
Сферический шарнир закрепляет одну точку тела и допускает лишь его поворот вокруг этой точки. Точно также и подпятник не допускает перемещения связанной точки тела. Поэтому реакции этих связей направляются произвольным образом в пространстве. При решении задач вычисляют проекции реакций сферического шарнира и подпятника на оси координат, как это показано на рисунке 5.4.
  Пример решения задачи типа С-5
Дано: AB = 1 м; BC = 2 м; P = 9 кН; q = 12 кН/м, G=10 кН. Определить: реакции связей. Решение.
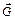 прикладываем к центру масс (геометрическому центру). Равномерно распределенную нагрузку заменяем сосредоточенной силой прикладываем к центру масс (геометрическому центру). Равномерно распределенную нагрузку заменяем сосредоточенной силой 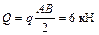 . Силу . Силу 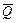 прикладываем в центре распределения нагрузки. прикладываем в центре распределения нагрузки.
Из рисунка 5.7 видно, что g – угол между проекцией силы Замечание.Для составления уравнений равновесия можно изобразить чертеж пластины в проекциях на координатные плоскости (рисунок 5.8). Тогда по проекции на плоскость zOy можно составить уравнения (см. рисунок 5.5, а):
Аналогично по проекциям на плоскость xOz (см. рисунок 5.8, б):
и плоскость xOy (рисунок 5.8, в):
Предоставляем читателю возможность самостоятельно убедиться в правильности уравнений (5.1)–(5.6), составленных с использованием описанного подхода.

4 Решаем полученную систему уравнений. Из уравнения (5.5) находим
Из уравнения (5.6) имеем
Уравнение (5.4) дает
Знак «минус», получившийся при расчете реакции RDz, показывает, что ее действительное направление противоположно изображенному на рисунке 5.2. Из уравнений (5.3), (5.2) и (5.1) находим оставшиеся неизвестные:
Равнодействующая силы реакции сферического шарнира A
Равнодействующая силы реакции цилиндрического шарнира D
5.3 Условие задания С-5 |
|
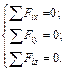
 В тех случаях, когда в условии задачи отсутствует известный угол между вектором силы и осью, часто используют метод двойного проецирования. Суть его заключается в следующем. Сначала определяют проекцию вектора силы на координатную плоскость, угол между которой и вектором силы известен. Затем ее, в свою очередь, проецируют на координатные оси.
В тех случаях, когда в условии задачи отсутствует известный угол между вектором силы и осью, часто используют метод двойного проецирования. Суть его заключается в следующем. Сначала определяют проекцию вектора силы на координатную плоскость, угол между которой и вектором силы известен. Затем ее, в свою очередь, проецируют на координатные оси. спроецирован вначале на плоскость xy, а затем на координатные оси x и y:
спроецирован вначале на плоскость xy, а затем на координатные оси x и y: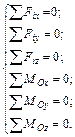
 Момент силы относительно оси считается положительным, если при наблюдении с конца оси видно, что сила стремится повернуть тело против хода часовой стрелки. При действии по ходу часовой стрелки момент считается отрицательным.
Момент силы относительно оси считается положительным, если при наблюдении с конца оси видно, что сила стремится повернуть тело против хода часовой стрелки. При действии по ходу часовой стрелки момент считается отрицательным. .
. Как и в случае нахождения момента силы относительно точки, так и для определения момента силы относительно оси, при необходимости можно применить теорему Вариньона, согласно которой момент равнодействующей силы относительно оси равен алгебраической сумме моментов слагаемых сил относительно той же оси.
Как и в случае нахождения момента силы относительно точки, так и для определения момента силы относительно оси, при необходимости можно применить теорему Вариньона, согласно которой момент равнодействующей силы относительно оси равен алгебраической сумме моментов слагаемых сил относительно той же оси. В пространственных конструкциях встречаются два вида шарниров: цилиндрический и сферический.
В пространственных конструкциях встречаются два вида шарниров: цилиндрический и сферический. Цилиндрический шарнир (подшипник) не допускает перемещения связываемого тела в плоскости, перпендикулярной оси шарнира. Поэтому его реакция лежит в этой плоскости. При решении задач рассчитывают проекции реакции цилиндрического шарнира на две оси координат (рисунок 5.3).
Цилиндрический шарнир (подшипник) не допускает перемещения связываемого тела в плоскости, перпендикулярной оси шарнира. Поэтому его реакция лежит в этой плоскости. При решении задач рассчитывают проекции реакции цилиндрического шарнира на две оси координат (рисунок 5.3). Заделка запрещает линейные и угловые перемещения по любому направлению. Поэтому реакция заделки в пространстве включает три проекции силы реакции на оси координат и три момента пар сил реакции относительно осей координат (рисунок 5.5).
Заделка запрещает линейные и угловые перемещения по любому направлению. Поэтому реакция заделки в пространстве включает три проекции силы реакции на оси координат и три момента пар сил реакции относительно осей координат (рисунок 5.5).
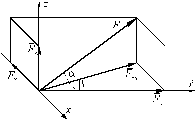
 Однородная плита АВСD (рисунок 5.6) находится под действием силы тяжести G, сосредоточенной силы
Однородная плита АВСD (рисунок 5.6) находится под действием силы тяжести G, сосредоточенной силы  и равномерно распределенной нагрузки интенсивности q.
и равномерно распределенной нагрузки интенсивности q. 2 Реакцию невесомого стержня EC, обозначенную буквой
2 Реакцию невесомого стержня EC, обозначенную буквой  , направляем вдоль стержня. Реакцию сферического шарнира A раскладываем на три составляющие: RAx, RAy, RAz. Реакцию цилиндрического шарнира D раскладываем на две составляющие: RDx, RDz. Начало системы координат помещаем в точку A, так как в ней сходятся линии действия трех из шести неизвестных сил.
, направляем вдоль стержня. Реакцию сферического шарнира A раскладываем на три составляющие: RAx, RAy, RAz. Реакцию цилиндрического шарнира D раскладываем на две составляющие: RDx, RDz. Начало системы координат помещаем в точку A, так как в ней сходятся линии действия трех из шести неизвестных сил. 3 Составляем уравнения равновесия плиты. Поскольку на нее действует произвольная пространственная система сил, то имеем шесть уравнений:
3 Составляем уравнения равновесия плиты. Поскольку на нее действует произвольная пространственная система сил, то имеем шесть уравнений: (5.1)
(5.1) (5.2)
(5.2) (5.3)
(5.3)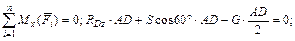 (5.4)
(5.4)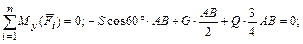 (5.5)
(5.5) . (5.6)
. (5.6) ,
, 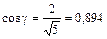 ,
,  . При определении момента силы
. При определении момента силы  относительно оси z применена теорема Вариньона.
относительно оси z применена теорема Вариньона.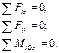
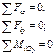
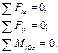


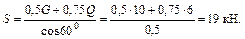
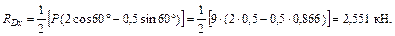
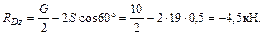
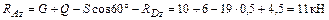 ;
; ;
;