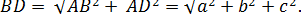Перпендикулярність прямих у просторі. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої та площини
(теорія і задачі)
Укладач:Петрова Т.В.,
вчитель Нижньосірогозької
ЗОШ І-ІІІ ступенів
1. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ У ПРОСТОРІ
Як і на площині, дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони теж перпендикулярні.
Доведення. Нехай а і b — перпендикулярні прямі,  і і  — паралельні їм прямі, які перетинаються. Доведемо, що прямі — паралельні їм прямі, які перетинаються. Доведемо, що прямі  і і  перпендикулярні. перпендикулярні.
Якщо прямі a, b  і і  лежать в одній площині, то вони мають зазначену в теоремі властивість, що відомо з планіметрії. лежать в одній площині, то вони мають зазначену в теоремі властивість, що відомо з планіметрії.
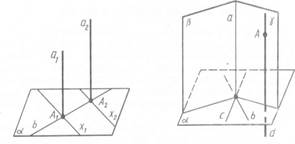
Припустимо тепер, що наші прямі не лежать в одній площині. Тоді прямі а і b лежать у деякій площині  , a прямі , a прямі  і і  — у якійсь площині — у якійсь площині  (мал. 1). (мал. 1).
За теоремою (якщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельня) площини  і і  паралельні. Нехай С — точка перетину прямих а і b, а паралельні. Нехай С — точка перетину прямих а і b, а  — точка перетину прямих — точка перетину прямих  і і  . .
Проведемо в площині паралельних прямих а і  , пряму, паралельну прямій , пряму, паралельну прямій  . Вона перетне прямі а і . Вона перетне прямі а і  в точках А і в точках А і 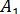 . У площині прямих b і . У площині прямих b і  проведемо пряму, паралельну прямій проведемо пряму, паралельну прямій  , і позначимо через В і , і позначимо через В і 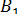 точки її перетину з прямими b і точки її перетину з прямими b і  . .
Чотирикутники  і і  — паралелограми, оскільки у них протилежні сторони паралельні. Чотирикутник — паралелограми, оскільки у них протилежні сторони паралельні. Чотирикутник  — теж паралелограм. У нього сторони — теж паралелограм. У нього сторони  , ,  паралельні, тому що кожна з них паралельна прямій паралельні, тому що кожна з них паралельна прямій  Таким чином, чотирикутник лежить у площині, яка проходить через паралельні прямі Таким чином, чотирикутник лежить у площині, яка проходить через паралельні прямі  і і  . А вона перетинає паралельні площини . А вона перетинає паралельні площини  і і  по паралельних прямих АВ і по паралельних прямих АВ і  . .
Оскільки в паралелограмі протилежні сторони рівні, то АВ =  , ,  |, ВС = |, ВС =  . За третьою ознакою рівності трикутників трикутники ABC і . За третьою ознакою рівності трикутників трикутники ABC і  рівні. Отже, кут рівні. Отже, кут  , який дорівнює куту АСВ, прямий, тобто прямі , який дорівнює куту АСВ, прямий, тобто прямі  і і  перпендикулярні. Теорему доведено. перпендикулярні. Теорему доведено.
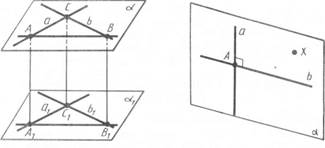
Мал. 1 Мал. 2
Задача (1). Доведіть, що через будь-яку точку прямої у просторі можна провести перпендикулярну до неї пряму.
Розв'язання. Нехай а — дана пряма й А — точка на ній (мал. 2). Візьмемо поза прямою а яку-небудь точку X і проведемо через цю точку і пряму а площину  ( Теорема: через пряму і точку,яка не лежить на ній, можна провести площину і до того ж тільки одну). У площині ( Теорема: через пряму і точку,яка не лежить на ній, можна провести площину і до того ж тільки одну). У площині  через точку А можна провести пряму b, перпендикулярну до прямої а. через точку А можна провести пряму b, перпендикулярну до прямої а.
2. ОЗНАКА ПЕРПЕНДИКУЛЯРНОСТІ ПРЯМОЇ І ПЛОЩИНИ
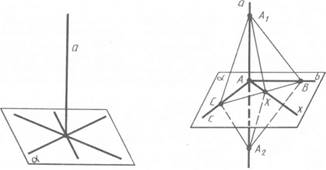
Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину (мал. 3).
Теорема 2. Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.
Мал. 3 Мал. 4 Доведення. Нехай а — пряма, перпендикулярна до прямих бісу площині  . .
Тоді пряма а проходить через точку А перетину прямих b і с (мал. 4). Доведемо, що пряма а перпендикулярна до площини  . .
Проведемо довільну пряму х через точку А у площині а і покажемо, що вона перпендикулярна до прямої а. Проведемо у площині  довільну пряму, яка не проходить через точку А і перетинає прямі b, с і х. Нехай точками перетину будуть В, С і X. Відкладемо на прямій а від точки А в різні боки рівні відрізки: довільну пряму, яка не проходить через точку А і перетинає прямі b, с і х. Нехай точками перетину будуть В, С і X. Відкладемо на прямій а від точки А в різні боки рівні відрізки:  і АА2. Трикутник і АА2. Трикутник  рівнобедрений, оскільки відрізок АС є висотою за умовою теореми і медіаною — за побудовою ( рівнобедрений, оскільки відрізок АС є висотою за умовою теореми і медіаною — за побудовою (  =АА2). З тієї ж причини трикутник =АА2). З тієї ж причини трикутник  теж рівнобедрений. Отже, трикутники теж рівнобедрений. Отже, трикутники  і А2ВС рівні за третьою ознакою рівності трикутників. і А2ВС рівні за третьою ознакою рівності трикутників.
З рівності трикутників  і А2ВС випливає рівність кутів і А2ВС випливає рівність кутів  ВХ, А2ВХ і, отже, рівність трикутників ВХ, А2ВХ і, отже, рівність трикутників  ВХ i А2ВХ за першою ознакою рівності трикутників. З рівності сторін ВХ i А2ВХ за першою ознакою рівності трикутників. З рівності сторін  Х і А2Х цих трикутників робимо висновок, що трикутник Х і А2Х цих трикутників робимо висновок, що трикутник  ХА2 рівнобедрений. Тому його медіана ХА є також висотою. А це означає, що – пряма х перпендикулярна до ХА2 рівнобедрений. Тому його медіана ХА є також висотою. А це означає, що – пряма х перпендикулярна до  . За означенням пряма а перпендикулярна до площини а . Теорему доведено. . За означенням пряма а перпендикулярна до площини а . Теорему доведено.
3. ПОБУДОВА ПЕРПЕНДИКУЛЯРНИХ ПРЯМОЇ І ПЛОЩИНИ
Задача (2). Доведіть, що через дану точку прямої можна провести одну і тільки одну перпендикулярну до неї площину.
Розв'язання. Нехай а — дана пряма і А — точка на ній (мал. 5). Проведемо через неї дві площини, а в них — через точку А прямі b і с, перпендикулярні до прямої а. Площина  , яка проходить через ці прямі, перпендикулярна до прямої а за теоремою 2. Доведемо, що ця площина єдина. Припустимо, що крім площини , яка проходить через ці прямі, перпендикулярна до прямої а за теоремою 2. Доведемо, що ця площина єдина. Припустимо, що крім площини  існує інша площина існує інша площина  ', яка проходить через точку А і перпендикулярна до прямої а (мал. 6). Нехай В — точка площини ', яка проходить через точку А і перпендикулярна до прямої а (мал. 6). Нехай В — точка площини  ', яка не лежить у площині а. Проведемо через точку В і пряму а площину. Вона перетне площини ', яка не лежить у площині а. Проведемо через точку В і пряму а площину. Вона перетне площини  і і  ' по різних прямих b і b', перпендикулярних до прямої а. А це, як ми знаємо, неможливо, оскільки на площині через дану точку прямої проходить тільки одна перпендикулярна до неї пряма. Отже, площина, яка проходить через точку А і перпендикулярна до прямої а,— єдина. ' по різних прямих b і b', перпендикулярних до прямої а. А це, як ми знаємо, неможливо, оскільки на площині через дану точку прямої проходить тільки одна перпендикулярна до неї пряма. Отже, площина, яка проходить через точку А і перпендикулярна до прямої а,— єдина.

Мал. 5 Мал. 6
Задача (2). Доведіть, що через дану точку площини можна провести одну і тільки одну перпендикулярну до неї пряму.
Розв'язання. Нехай  —дана площина і A – точка на ній (мал. 7). Проведемо у площині —дана площина і A – точка на ній (мал. 7). Проведемо у площині  через точку А дві прямі b і с. Проведемо через точку А перпендикулярні до них площини. Вони перетнуться по деякій прямій а, перпендикулярній до прямих b і с. Отже, пряма а перпендикулярна до площини через точку А дві прямі b і с. Проведемо через точку А перпендикулярні до них площини. Вони перетнуться по деякій прямій а, перпендикулярній до прямих b і с. Отже, пряма а перпендикулярна до площини  . Доведемо, що ця пряма єдина. Припустимо, що крім прямої а існує інша пряма а', яка проходить через точку А і перпендикулярна до площини . Доведемо, що ця пряма єдина. Припустимо, що крім прямої а існує інша пряма а', яка проходить через точку А і перпендикулярна до площини  (мал. 8). Проведемо через прямі а і а' площину. Вона перетне площину (мал. 8). Проведемо через прямі а і а' площину. Вона перетне площину  по деякій прямій b, перпендикулярній до прямих а і а'. А це неможливо. Отже, пряма, яка проходить через дану точку площини і перпендикулярна до цієї площини, єдина. по деякій прямій b, перпендикулярній до прямих а і а'. А це неможливо. Отже, пряма, яка проходить через дану точку площини і перпендикулярна до цієї площини, єдина.
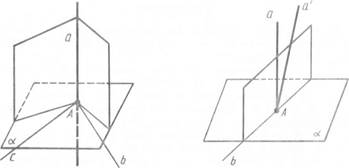
Мал. 7 Мал. 8
4. ВЛАСТИВОСТІ ПРЯМОЇ І ПЛОЩИНИ, ПЕРПЕНДИКУЛЯРНИХ МІЖ СОБОЮ
Теорема 3. Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.
Доведення. Нехай  і а2— дві паралельні прямі і і а2— дві паралельні прямі і  – площина, перпендикулярна до прямої – площина, перпендикулярна до прямої  (мал. 9). Доведемо, що ця площина перпендикулярна й до прямої а2. (мал. 9). Доведемо, що ця площина перпендикулярна й до прямої а2.
Проведемо через точку А2 перетину прямої а2 з площиною  довільну пряму х2 у площині довільну пряму х2 у площині  . Проведемо у площині . Проведемо у площині  через точку через точку  перетину прямої перетину прямої  з з  пряму пряму  , паралельну прямій х2. Оскільки пряма , паралельну прямій х2. Оскільки пряма  перпендикулярна до площини перпендикулярна до площини  , то прямі , то прямі  і і  перпендикулярні. А за теоремою 1 паралельні до них прямі а2 і х2, що перетинаються, теж перпендикулярні. Таким чином, пряма а2 перпендикулярна до будь-якої прямої х2 у площині перпендикулярні. А за теоремою 1 паралельні до них прямі а2 і х2, що перетинаються, теж перпендикулярні. Таким чином, пряма а2 перпендикулярна до будь-якої прямої х2 у площині  . А це означає, що пряма а2 перпендикулярна до площини . А це означає, що пряма а2 перпендикулярна до площини  . Теорему доведено. . Теорему доведено.
Мал. 9 Мал.10
Задача (4). Доведіть, що через будь-яку точку А можна провести пряму, перпендикулярну до даної площини  . Розв'язання. Проведемо у площині . Розв'язання. Проведемо у площині  дві прямі b і с, що перетинаються (мал. 10). Через точку їх перетину проведемо площини дві прямі b і с, що перетинаються (мал. 10). Через точку їх перетину проведемо площини 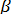 і і  , перпендикулярні до прямих b і с відповідно. Перетином їх буде пряма а. Пряма а перпендикулярна до прямих b і с, отже, і до площини , перпендикулярні до прямих b і с відповідно. Перетином їх буде пряма а. Пряма а перпендикулярна до прямих b і с, отже, і до площини  . Проведемо тепер через точку А пряму d, паралельну а. За теоремою 3 вона перпендикулярна до площини . Проведемо тепер через точку А пряму d, паралельну а. За теоремою 3 вона перпендикулярна до площини 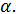
Теорема 4. Дві прямі, перпендикулярні до однієї і тієї самої площини, паралельні.
Доведення. Нехай а і b — дві прямі, перпендикулярні до площини  (мал.11). Припустимо, що прямі а і b не паралельні. Виберемо на прямій b точку С, що не лежить на площині (мал.11). Припустимо, що прямі а і b не паралельні. Виберемо на прямій b точку С, що не лежить на площині  . Проведемо через точку С пряму b', паралельну прямій а. Пряма b' перпендикулярна до площини . Проведемо через точку С пряму b', паралельну прямій а. Пряма b' перпендикулярна до площини  (теорема 3). Нехай В і В' — точки перетину прямих b і b' з площиною а. Тоді пряма ВВ' перпендикулярна до прямих b і b', які перетинаються. А це неможливо. Ми прийшли до суперечності. Теорему доведено. (теорема 3). Нехай В і В' — точки перетину прямих b і b' з площиною а. Тоді пряма ВВ' перпендикулярна до прямих b і b', які перетинаються. А це неможливо. Ми прийшли до суперечності. Теорему доведено.
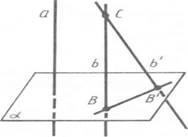
Мал. 11
Задача (6). Прямі AB, AC і AD попарно перпендикулярні. Знайдіть відрізок CD якщо: 1) AB =3 см, BC =7 см , AD = 1,5 см ; 2) BD = 9 см , BC= 16 см , AD = 5 см ; 3) AB =a, BC =b, AD = c;
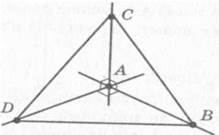
Мал. 12
Розв'язання. За умовою 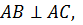   отже, отже,   – прямокутні (мал. 12). Знайдемо довжину сторони DC. – прямокутні (мал. 12). Знайдемо довжину сторони DC.
1) З  ( (   (см2) З (см2) З 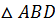 ( (   (см) (см)
2) З 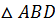 ( (   (см2) (см2)
З  ( (   (см2) З (см2) З  ( (   (см) (см)
3) З  ( (   З З  ( (  
відповідь: 1)  см; 2) см; 2)  см; 3) см; 3)  . .
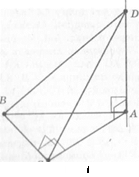 Задача (7). Через вершину гострого кута прямокутного трикутника Задача (7). Через вершину гострого кута прямокутного трикутника  з прямим кутом С проведено пряму з прямим кутом С проведено пряму  , перпендикулярну до площини трикутника. Знайдіть відстань від точки , перпендикулярну до площини трикутника. Знайдіть відстань від точки  до вершин В і С, якщо AС =a, BC =b, AD = c. до вершин В і С, якщо AС =a, BC =b, AD = c.
Мал. 13
Розв'язання.І спосіб
Через вершину А гострого кута прямокутного 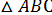 ( (  проведено пряму AD, яка перпендикулярна до площини проведено пряму AD, яка перпендикулярна до площини  (мал. 13). За умовою АС = а, ВС = b, AD = с. Знайдемо відстані від точки D до вершин В і С. (мал. 13). За умовою АС = а, ВС = b, AD = с. Знайдемо відстані від точки D до вершин В і С.
З   . Оскільки AD — перпендикуляр до площини трикутника ABC, to . Оскільки AD — перпендикуляр до площини трикутника ABC, to  і і  (означення прямої, перпендикулярної до площини). Отже, (означення прямої, перпендикулярної до площини). Отже,  і і  — прямокутні. Тому — прямокутні. Тому
 i i 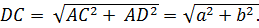
ІI спосіб
За умовою AD — перпендикуляр до площини 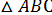 , тобто , тобто  (означення прямої, перпендикулярної до площини). Тоді (означення прямої, перпендикулярної до площини). Тоді  AD — перпендикуляр до площини AD — перпендикуляр до площини 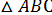 , ВС — похила до цієї площини, AС - її проекція на площину , ВС — похила до цієї площини, AС - її проекція на площину 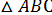 . За умовою . За умовою 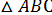 — прямокутний, в якому — прямокутний, в якому  АС = = 90°, тобто АС = = 90°, тобто  . Тоді за теоремою про три перпендикуляри . Тоді за теоремою про три перпендикуляри  . Звідси . Звідси 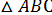 — прямокутний — прямокутний  СВ = 90°). Тому СВ = 90°). Тому 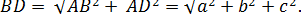
|

 і
і  — паралельні їм прямі, які перетинаються. Доведемо, що прямі
— паралельні їм прямі, які перетинаються. Доведемо, що прямі  перпендикулярні.
перпендикулярні. і
і  , a прямі
, a прямі  — у якійсь площині
— у якійсь площині  (мал. 1).
(мал. 1). паралельні. Нехай С — точка перетину прямих а і b, а
паралельні. Нехай С — точка перетину прямих а і b, а  — точка перетину прямих
— точка перетину прямих  . Вона перетне прямі а і
. Вона перетне прямі а і  в точках А і
в точках А і 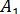 . У площині прямих b і
. У площині прямих b і 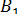 точки її перетину з прямими b і
точки її перетину з прямими b і  і
і 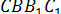 — паралелограми, оскільки у них протилежні сторони паралельні. Чотирикутник
— паралелограми, оскільки у них протилежні сторони паралельні. Чотирикутник  — теж паралелограм. У нього сторони
— теж паралелограм. У нього сторони  ,
,  паралельні, тому що кожна з них паралельна прямій
паралельні, тому що кожна з них паралельна прямій  Таким чином, чотирикутник лежить у площині, яка проходить через паралельні прямі
Таким чином, чотирикутник лежить у площині, яка проходить через паралельні прямі  .
. |, ВС =
|, ВС =  . За третьою ознакою рівності трикутників трикутники ABC і
. За третьою ознакою рівності трикутників трикутники ABC і  рівні. Отже, кут
рівні. Отже, кут  , який дорівнює куту АСВ, прямий, тобто прямі
, який дорівнює куту АСВ, прямий, тобто прямі 
 рівнобедрений, оскільки відрізок АС є висотою за умовою теореми і медіаною — за побудовою (
рівнобедрений, оскільки відрізок АС є висотою за умовою теореми і медіаною — за побудовою (  теж рівнобедрений. Отже, трикутники
теж рівнобедрений. Отже, трикутники  і А2ВС рівні за третьою ознакою рівності трикутників.
і А2ВС рівні за третьою ознакою рівності трикутників.

 , паралельну прямій х2. Оскільки пряма
, паралельну прямій х2. Оскільки пряма 
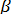 і
і  , перпендикулярні до прямих b і с відповідно. Перетином їх буде пряма а. Пряма а перпендикулярна до прямих b і с, отже, і до площини
, перпендикулярні до прямих b і с відповідно. Перетином їх буде пряма а. Пряма а перпендикулярна до прямих b і с, отже, і до площини 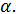
 (мал.11). Припустимо, що прямі а і b не паралельні. Виберемо на прямій b точку С, що не лежить на площині
(мал.11). Припустимо, що прямі а і b не паралельні. Виберемо на прямій b точку С, що не лежить на площині  . Проведемо через точку С пряму b', паралельну прямій а. Пряма b' перпендикулярна до площини
. Проведемо через точку С пряму b', паралельну прямій а. Пряма b' перпендикулярна до площини 

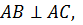

 отже,
отже, 
 – прямокутні (мал. 12). Знайдемо довжину сторони DC.
– прямокутні (мал. 12). Знайдемо довжину сторони DC. (
( 
 (см2) З
(см2) З 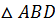 (
( 
 (см)
(см)
 (см2)
(см2) (см2) З
(см2) З  (
( 
 (см)
(см) З
З  (
( 
 см; 2)
см; 2)  см; 3)
см; 3)  .
. Задача (7). Через вершину гострого кута прямокутного трикутника
Задача (7). Через вершину гострого кута прямокутного трикутника  з прямим кутом С проведено пряму
з прямим кутом С проведено пряму  , перпендикулярну до площини трикутника. Знайдіть відстань від точки
, перпендикулярну до площини трикутника. Знайдіть відстань від точки  до вершин В і С, якщо AС =a, BC =b, AD = c.
до вершин В і С, якщо AС =a, BC =b, AD = c.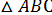 (
(  проведено пряму AD, яка перпендикулярна до площини
проведено пряму AD, яка перпендикулярна до площини  (мал. 13). За умовою АС = а, ВС = b, AD = с. Знайдемо відстані від точки D до вершин В і С.
(мал. 13). За умовою АС = а, ВС = b, AD = с. Знайдемо відстані від точки D до вершин В і С.
 . Оскільки AD — перпендикуляр до площини трикутника ABC, to
. Оскільки AD — перпендикуляр до площини трикутника ABC, to  і
і  (означення прямої, перпендикулярної до площини). Отже,
(означення прямої, перпендикулярної до площини). Отже,  і
і  — прямокутні. Тому
— прямокутні. Тому i
i 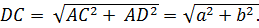
 (означення прямої, перпендикулярної до площини). Тоді
(означення прямої, перпендикулярної до площини). Тоді  AD — перпендикуляр до площини
AD — перпендикуляр до площини  АС = = 90°, тобто
АС = = 90°, тобто  . Тоді за теоремою про три перпендикуляри
. Тоді за теоремою про три перпендикуляри  . Звідси
. Звідси  СВ = 90°). Тому
СВ = 90°). Тому