|
|
Электрическое поле. Напряженность электрического поляЗакон Кулона. Закон, которому подчиняется сила взаимодействия точечных зарядов, был установлен экспериментально в 1785 году Кулоном. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд. Кулон измерял силу взаимодействия двух заряженных шариков в зависимости от величины зарядов на них и расстояния между ними и пришел к выводу, что сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Закон Кулона выражается формулой:
где k - коэффициент пропорциональности; q1 и q2 - величины взаимодействующих зарядов; r - расстояние между зарядами; r - радиус-вектор от одного заряда к другому. В случае одноименных зарядов сила Fоказывается положительной, что соответствует отталкиванию между зарядами. В случае разноименных зарядов сила отрицательна, что соответствует притяжению зарядов друг к другу. Закон Кулона справедлив от расстояний 10-15 м и до нескольких километров. В международной системе единиц (СИ) коэффициент пропорциональности k в законе Кулона равен
Величину называют электрической постоянной, она имеет размерность электрической емкости, деленной на длину, и равна:
Подобная запись формулы называется рационализованной, a СИ принадлежит к рационализованным системам единиц. Закон Кулона для силы взаимодействия зарядов в однородной диэлектрической среде в СИ имеет вид:
где Результирующая сила
Т.е. определяется векторной суммой сил действующих, на данный заряд q со стороны каждого из зарядов qi Электрическое поле. Напряженность электрического поля
Взаимодействие между покоящимися зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку заряд оказывается под действием силы. Следовательно, для обнаружения и исследования электрического поля нужно воспользоваться некоторым пробным зарядом q. Согласно закону Кулона на пробный заряд действует сила
Отношение
Эту векторную величину называют напряженностью электрического поля в данной точке. Напряженность электрического поля численно равна силе, действующей на единичный точечный заряд, находящийся в данной точке поля. Направление вектора Напряженность поля точечного заряда пропорциональна величине заряда qи обратно пропорциональна квадрату расстояния r от заряда до данной точки поля
Направлен вектор
Согласно приведенной формуле, сила, действующая на пробный заряд
Очевидно, что на всякий точечный заряд q в точке поля с напряженностью
Если заряд положителен, направление силы совпадает с направлением вектора Было указано ранее, что сила, с которой система зарядов действует на некоторый, не входящий в систему заряд равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы в отдельности (4). Отсюда вытекает, что напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности:
Это принцип суперпозиции (наложения электрических полей). Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов. Линии напряженности. Поток вектора напряженности. Электрическое поле можно описать определив для каждой точки величину и направление вектора Линии
Следовательно, N равно
Поскольку густота линий
Где
которое называется потоком вектора
|
|
 (2)
(2) и выражение закона Кулона для зарядов в вакууме приобретает вид:
и выражение закона Кулона для зарядов в вакууме приобретает вид: .
. Ф/М.
Ф/М.
 (3)
(3)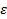 - относительная диэлектрическая проницаемость среды.
- относительная диэлектрическая проницаемость среды. , о которой действует на данный заряд
, о которой действует на данный заряд  система N зарядов
система N зарядов  , определяется:
, определяется: , (4)
, (4) .
. для всех пробных зарядов будет одним и тем же и зависит лишь от величин q и r , определяющих поле в данной точке. Поэтому естественно принять это отношение в качестве величины, характеризующей электрическое поле:
для всех пробных зарядов будет одним и тем же и зависит лишь от величин q и r , определяющих поле в данной точке. Поэтому естественно принять это отношение в качестве величины, характеризующей электрическое поле: (5)
(5) совпадает с направление силы, действующей на положительный заряд.
совпадает с направление силы, действующей на положительный заряд. (6)
(6) .
.
 (7)
(7) и ?
и ? 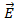 противоположны.
противоположны. (8)
(8) . Густота линий по условию численно равна:
. Густота линий по условию численно равна: 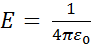 .
.
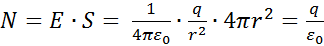
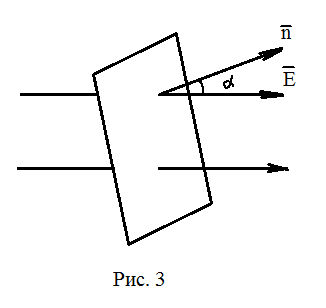 Число линий на любом расстоянии от заряда будет одно и то же. Отсюда вытекает, что силовые линии нигде, кроме заряда, не начинаются и не заканчиваются. Линии начавшись на положительном заряде, уходят в бесконечность, либо, приходя из бесконечности, заканчиваются на отрицательном заряде. Это свойство линий
Число линий на любом расстоянии от заряда будет одно и то же. Отсюда вытекает, что силовые линии нигде, кроме заряда, не начинаются и не заканчиваются. Линии начавшись на положительном заряде, уходят в бесконечность, либо, приходя из бесконечности, заканчиваются на отрицательном заряде. Это свойство линий  , перпендикулярную вектору
, перпендикулярную вектору 
 – составляющая вектора
– составляющая вектора  , (10)
, (10) и, следовательно, у N .
и, следовательно, у N .