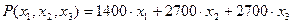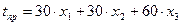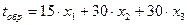|
|
Транспортные задачи, логистика и задачи о назначенияхА.А. Балабанов Лабораторный практикум по курсу
Утверждено редакционно-издательским советом института
Москва 2011 УДК 330.45(075.8) ББК 65в631я М62 Рецензент доц., к.ф.-м.н. А.М. Ревякин Балабанов А.А. Лабораторный практикум по курсу «Исследование операций», М.: МИЭТ, 2011.-135с.: ил. Курс «Исследование операций» (OperationsResearch) является обязательной частью любой серьезной программы профессиональной подготовки и переподготовки современных управленцев. В нем рассматриваются модели и методы оптимизации управления и принятия решений, развитые за почти сто лет, прошедшие с момента появления научного менеджмента. Оптимальные планы производства, продаж, закупок, перевозок, агрегатное планирование, управление запасами и проектами, организация работы и оценка эффективности систем массового обслуживания – вот далеко не полный перечень применений количественных методов исследования операций. Количественные методы исследования операций предоставляют мощные инструменты анализа в области финансового планирования, оптимизации инвестиционных портфелей, для оценки и управления финансовыми рисками, прогнозирования ценообразования производных ценных бумаг и пр. Лабораторный практикум содержит описания 9 лабораторных работ, включающих теоретические основы и рекомендации по их выполнению. Тематика работ охватывает базовые количественные методы исследования операций. Основной акцент в работах сделан не на математической стороне проблемы, не на детальном рассмотрении вопроса о том, как получить решение поставленной математической задачи, а на выработку навыков правильно применять готовые компьютерные программы, хорошо разработанную технику анализа количественных моделей управления для принятия эффективных управленческих решений.
© МИЭТ, 2011 Лабораторная работа №1. Теоретические основы С помощью моделей линейной оптимизации решаются задачи составления оптимальных планах производства, продаж, закупок, перевозок, об оптимальном финансовом планировании, оптимальной организации рекламной кампании и др. При постановке любой задачи оптимизации необходимо, прежде всего, определить количественную характеристику достигаемой цели – целевую функцию. Это может быть максимум прибыли или минимум издержек (в денежном, временном или каком-либо другом выражении). Целевая функция показывает, почему одно рассматриваемое решение лучше или хуже другого. Целевая функция зависит от величин, называемых переменными решения. Цель оптимизации найти такие значения переменных решения, при которых целевая функция максимальна или минимальна. Любая оптимизация всегда проводится при наличии некоторых ограничений – условий, ограничивающих изменения переменных решения при поиске максимальной или минимальной целевой функции. Эти ограничения могут диктоваться: · ограниченностью ресурсов (денежных, временных, материальных); · установленными «правилами игры» (рыночные ограничения, нормативные акты, лимитирующие ту или иную характеристику или любые требования субъекта, принимающего решения). Линейное оптимизация имеет дело с моделями, в которых целевая функция Фактически, это означает, что целевая функция и ограничения могут представлять собой только суммы произведений постоянных коэффициентов на переменные решения в первой степени, т.е. выражения типа
Задачи линейной оптимизации могут быть решены, и реально многие годы решались, симплекс-методом. Однако, с точки зрения быстрейшего достижения цели, рационально использовать возможности современных компьютерных приложений, в частности, надстройку «Поиск решения» (в английском варианте – Solver) приложения MS Excel. Все задачи в данном сборнике лабораторных работ будут решены именно с помощью этой надстройки. Это, однако, не должно удерживать читателя от использования других средств. Примеры решения задач Пример 1.1 Задача планирования производства Фирма «Фасад» производит двери для продажи местным строительным компаниям. Репутация фирмы позволяет ей продавать всю производимую продукцию. На фирме работает 10 рабочих в одну смену (8 рабочих часов), 5 дней в неделю, что дает 400 часов в неделю. Рабочее время поделено между двумя существенно различными технологическими процессами: собственно производством и конечной обработкой дверей. Из 400 рабочих часов в неделю 250 отведены под собственно производство и 150 под конечную обработку. «Фасад» производит 3 типа дверей: стандартные, полированные и резные. В таблице приведены временные затраты и прибыль от продажи одной двери каждого типа.
1. Сколько дверей различных типов нужно производить, чтобы максимизировать прибыль? 2. Оптимально ли распределение рабочего времени между двумя технологическими процессами (производство и конечная обработка)? Как изменится прибыль, если распределить рабочее время между этими процессами оптимально? 3. На предстоящей неделе «Фасад» должен выполнить контракт на поставку 200 стандартных, 120 полированных и 80 резных дверей. Для выполнения заказа «Фасад» может закупить некоторое количество полуфабрикатов дверей у внешнего поставщика. Эти полуфабрикаты «Фасад» может использовать только для производства стандартных и полированных, но не резных дверей. При этом изготовление стандартной двери требует лишь 6 мин процесса обработки, а полированной – 20 мин обработки (процесс собственно производства для этих полуфабрикатов не требуется). Полученная таким образом стандартная дверь приносит 450 руб. прибыли, а полированная – 1600 руб. Предполагая, что по-прежнему 250 часов в неделю отведено под производство и 150 под обработку, определите, сколько и каких дверей «Фасад» должен произвести самостоятельно, и сколько полуфабрикатов закупить для изготовления стандартных и полированных дверей? 4. Как изменится оптимальный план, полученный при выполнении предыдущего пункта, если правильно распределить время между собственно производством и обработкой дверей? Каково будет правильное распределение в данном случае? # Решение задачи. 1. Прежде всего, определим цель задачи и вид целевой функции. В данном случае мы хотим максимизировать прибыль, следовательно, целевая функция должна вычислять полную прибыль. В задаче не приводится сведений об издержках и выручке, а задана прибыль, которую приносит каждая произведенная дверь. Поэтому полная прибыль P будет определяться этой прибылью и тем, сколько дверей произведено. Эти соображения приводят нас к выводу, что в качестве переменных задачи следует выбрать количества дверей каждого типа, которые следует произвести. Значит, в задаче будет 3 переменных: x1 - количество стандартных дверей, x2 – количество полированных и x3 – количество резных дверей. При этом целевая функция запишется, очевидно, следующим образом:
Рационально организовать данные на листе MS Excel следующим образом (Рис.1):
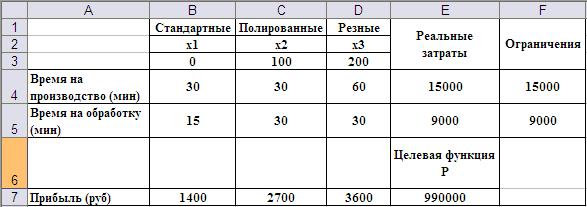
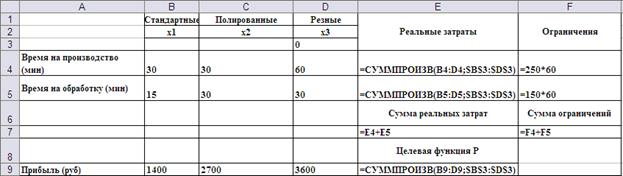
Рис.1. Организация данных и введённые формулы для решения пункта 1 задачи примера 1.1. Фрагмент рабочего листа на Рис.1.1 изображён в режиме показа формул. Формулы в ячейки рационально вводить следующим образом. В начале в ячейку E4 вводят формулу =СУММПРОИЗВ(B4:D4;$B$3:$D$3). Эта формула позволяет рассчитать реальные временные затраты на производство дверей
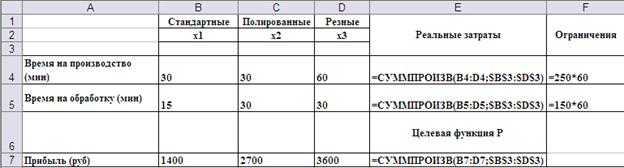
Блок ячеек $B$3:$D$3, выделенный под значения переменных x1, x2 и x3, адресован абсолютно. Это позволяет ввести формулы для расчёта времени на обработку
и целевой функции
в ячейки E5 и E7, соответственно, путём копирования формулы в ячейке E4. При этом массивы коэффициентов будут автоматически меняться, а массив переменных оставаться неизменным. В ячейки F4 и F5 введены ограничения по времени производства и обработки в минутах (множитель 60 в формулах). Теперь имеется вся информация, необходимая надстройке «Поиск решения» для определения оптимального по прибыли плана производства. В строке меню находим пункт Сервис (Tools), а внутри выпадающего меню пункт Поиск решения (в английской версии программы Solver). Вызов надстройки «Поиск решения» приводит к появлению следующего диалогового окна (Рис.2):
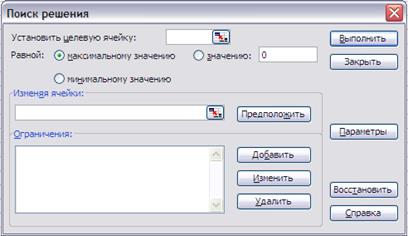
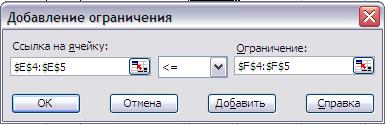
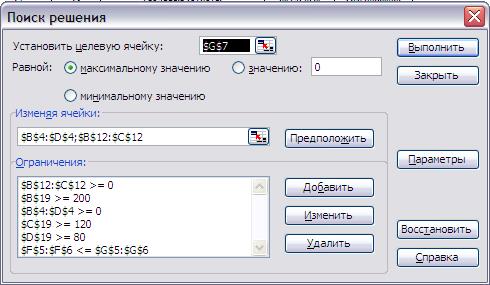
Рис.2. Диалоговое окно надстройки «Поиск решения» В нем и следует задать параметры поиска. В окне «Установить целевую ячейку» необходимо указывать ячейку, содержащую целевую функцию (нашем примере, как видно по Рис. 1, это ячейка E7). Переключатель оставляем в позиции Равной максимальному значению. В окошке «Изменяя ячейки» нужно указать ячейки, содержащие переменные решения – в нашем случае это B3:D3. Чтобы указать несколько ячеек, просто выделяем диапазон, как обычно это делается в Excel (в случае разрозненных ячеек удерживая клавишу Ctrl на клавиатуре). Для того, чтобы добавить что-либо в окно Ограничения, следует нажать кнопку «Добавить» и в выпадающем окне (Рис. 3) ввести ограничения
Рис.3. Диалоговое окно ввода ограничений на переменные. В данном случае записано, что числа в ячейках E4:E5 меньше или равны числам в ячейках F4:F5, соответственно. Эта установка, таким образом, описывает систему временных ограничений
К этим ограничениям необходимо добавить ограничения на неотрицательность и целочисленность переменных. Результат всех этих действий показан на рисунке (Рис.4).
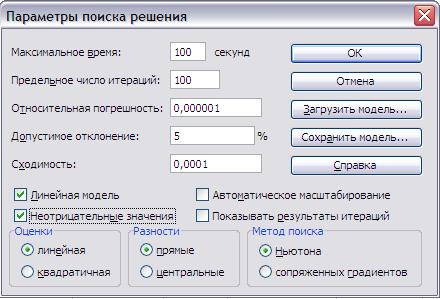
Рис.4. Окончательный вид диалогового окна надстройки «Поиск решения». До запуска надстройки на поиск нужно еще, нажав кнопку Параметры, вызвать панель Параметров поиска решения (Рис.5) и отметить галочками в соответствующих окошках, что задача соответствует линейной модели.
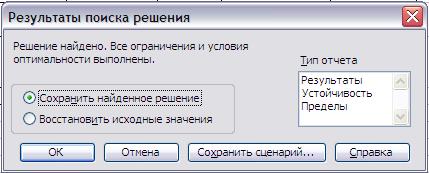
Рис.5. Установка параметров надстройки «Поиск решения». Больше никаких изменений здесь делать не нужно. Нажав ОК, возвращаемся в панель «Поиск решения». Теперь можно нажимать кнопку «Выполнить», после чего и будет найдено решение, о чем и сообщит панель Результаты поиска решения (Рис.6).
Рис.6. Окно результатов поиска решений. Нажав ОК, сохраняем найденное решение на листе MS Excel, содержащем условия задачи.
Рис.7. Окончательные результаты решения задачи по пункту 1. В данном случае оказывается, что максимально возможная прибыль равна 990000 руб. и получена она будет, если производить за неделю 100 полированных дверей и 200 резных. Это и есть оптимальный план производства для базовой задачи (пункт 1). 2. В первой части задачи мы полагали, что суммарное рабочее время по каким-то причинам (не упоминаемым в условии задачи) жестко разбито на 250 часов производства и 150 часов обработки. Возможно, что это связано со специализацией рабочих. Тем не менее, можно попробовать выяснить, каково оптимальное распределение рабочего времени между стадиями? Ведь если выигрыш от некоторого, возможного на практике, изменения условий значителен, будет иметь смысл приложить определенные усилия и реорганизовать работу. Оставим действующим решение задачи, и для модифицированной задачи создадим новый лист. (Имеет смысл создать копию листа, щелкнув правой кнопкой по ярлычку листа и отметив пункт «Переместить/Скопировать», а затем поставив флажок «Создавать копию». Во время этой процедуры копируется и скрытый лист с установками для надстройки «Поиск решения»). Для изменения условий в исходную таблицу добавим две строки: одна с заголовками, другая с формулами суммирования реальных временных затрат E7 и временных ограничений F7 (Рис.8).
Рис.8. Организация данных и введённые формулы для решения пункта 2 задачи примера 1.1. После этого нужно немного модифицировать задание надстройке «Поиск решения». Вызвав надстройку, удалим из ограничений условие $E$4:$E$5 <= $F$4:$F$5, и добавим вместо него условие E7 <= F7. Получим следующее решение (Рис. 9)
Рис.9. Окончательные результаты решения задачи по пункту 2. Распределение времени на производство и на обработку изменилось. Кроме того отметим, во-первых, что максимальная общая прибыль выросла на 180000 руб. в неделю. Во-вторых, оптимальный план рекомендует выпускать только полированные двери в количестве 400 штук. Применительно к реальной ситуации вызывает некоторые подозрения рекомендация совсем не выпускать двери первого и третьего типов. Понятно, что условия задачи отвечают ситуации, когда рынок дверей сильно не насыщен, но при этом существуют другие поставщики дверей разных типов. Сужение ассортимента может осложнить позиции фирмы в конкурентной борьбе, особенно при условии ограниченных производственных возможностях фирмы (суммарное время на производство и обработку ограниченно). Поэтому имеет смысл посмотреть, что меняется, если потребовать выпускать все двери. Конечно, здесь нужно задать некоторое конкретное число, которое мы вынуждены «взять с потолка». Положим, что следует выпускать не менее 50 штук дверей каждого типа. Для этого необходимо изменить опции настройки «Поиск решения», как показано на Рис. 10.
Рис.10. Настройка опций поиска решений при ограничениях на выпуск не менее 50 штук каждого изделия. Получим новое решение задачи (Рис.11).
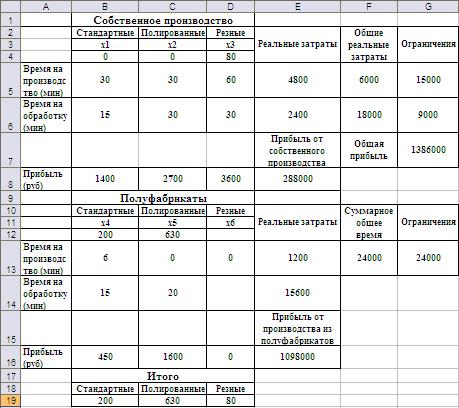
Рис.11. Окончательные результаты решения задачи при ограничениях на выпуск не менее 50 штук каждого изделия. Введенное ограничение, как любое новое ограничение задачи, уменьшает итоговую прибыль с 990000 руб. до 970000 руб. Конечно, только что проведенное исследование задачи не требуется по условию, но зачастую такой анализ («что будет, если…») очень интересен и полезен для принятия разумного управленческого решения при использовании той или иной математической модели. 3. Новые условия, описанные в пункте с, усложняют задачу. Чтобы их учесть следует ввести две новые переменные: количество стандартных дверей и количество полированных дверей, изготовленных из полуфабрикатов стороннего поставщика. Кроме этого нужно учесть размер заказа и потребовать безусловного его выполнения. Организация данных на листе MS Excel в этом случае представлена на Рис.12.
Рис.12. Организация данных и введённые формулы для решения пункта 3 задачи примера 1.1. На Рис. 13 показана настройка опций поиска решения.
Рис.13. Вид диалогового окна для настройки опций поиска решения пункта 3 задачи примера 1.1. Результаты примера (Рис.14) свидетельствуют о выполнении всех ограничений.
Рис.14. Окончательные результаты решения задачи по пункту 3. 4. Для решения этой задачи нужно изменить только одно условие – так же как было сделано при анализе части 2 задачи, ограничено только суммарное время двух стадий. Результат представлен на Рис.15.
Рис.15. Окончательные результаты решения задачи по пункту 4. Задачи для самостоятельного решения Электронные переключатели Фирма производит три вида электронных переключателей. Каждый тип требует сборку, состоящую из двух стадий. Время необходимое для сборки на каждой стадии приведено в таблице.
Оборудование для каждой стадии работает 7,5 часов в день. Менеджер хочет максимизировать прибыль за следующие 5 рабочих дней. Модель А дает прибыль $8.25 за штуку. Модель B дает прибыль $7.00 за штуку. Модель С дает прибыль $7.80 за штуку. Фирма может продавать все, что она произведет, и, кроме того, имеет на следующую неделю оплаченный заказ на 60 шт.: по 20 шт. устройств каждого типа. 1. Каков должен быть оптимальный производственный план? 2. Все ли типы моделей выгодно производить? Если имеется убыточная модель, то что нужно изменить, чтобы ее производство стало выгодным? Можно ли изменить что-нибудь в технологии или в ценовой политике так, чтобы все модели стали выгодными? Попробуйте сделать это. Подробно опишите результаты Ваших исследований. 3. Допустим, Вы можете установить 2 сверхурочных часа для одной из стадий. Для какой именно стадии следует назначить эти сверхурочные часы, чтобы получить наибольшую прибыль? Подтвердите все ваши ответы вычислениями.
Предприятие «Высокий октан» Нефтеперерабатывающее предприятие должно произвести не менее 8 000 тонн обычного бензина с октановым числом 85 и не менее 5 000 тонн высокооктанового с октановым числом 95. Товарный бензин с заданным октановым числом получается путем смешивания нескольких сортов первичного бензина, получающегося при перегонке. Для получения первичных бензинов в рассматриваемый период можно использовать три сорта сырой нефти от поставщиков с Южного Урала, с Каспийского моря и из Сибири. Среднее октановое число первичного бензина и его количество, получаемые при перегонке каждого сорта нефти, доступные в рассматриваемый период времени, а также себестоимость тонны первичного представлены в таблице.
В рассматриваемый период доступные производственные мощности предприятия «Высокий октан» позволяют произвести 15 000 тонн бензина. Предприятие продает обычный бензин по цене 7 000 руб. за тонну, а высокооктановый – по цене 8 000 руб. за тонну. По технологии обычный бензин должен иметь октановое число не ниже 85, а высокооктановый бензин – не ниже 95. 1. Допуская, что октановое число товарного бензина равно взвешенному среднему октановых чисел первичных бензинов, из которых он получен, найти оптимальные количества каждого сорта первичного бензина, необходимые для производства обоих видов товарного бензина в рассматриваемый период. Предположите, что весь произведенный бензин может быть продан. 2. Предположим, что предприятие может высвободить дополнительные мощности для производства 3000 тонн бензина за счет приостановки работы по другим контрактам. Приостановка работ по этим контрактам ведет к штрафу в 5 млн. руб. Стоит ли компании заплатить этот штраф и высвободить дополнительные мощности для рассматриваемого проекта? 3. Предположим, что поставщик нефти из Сибири, имея излишки нефти и нуждаясь в денежных средствах, желает заключить контракт с «Высоким октаном» на поставку 12 000 тонн нефти по цене 3350 руб. за условную тонну. Выгодно ли для «Высокого октана» принять это предложение? Получит ли поставщик больше денег в результате этой сделки? (Примите, что ограничение в 15 000 тонн действует). 4. Поставщик с Южного Урала, заплатив всего 200 долларов, получил информацию о том, что предложение сибирского поставщика принято. Так как ему абсолютно очевидно, что после переработки сибирской нефти нужда в южноуральской нефти возрастет, поставщик предлагает «Высокому октану» купить еще 1000 тонн его нефти по цене 2700 руб. за тонну. Выгодно ли принять это предложение с учетом высвобождения дополнительных мощностей (см. пункт 2)?
Собачья еда Компания производит три вида еды для животных: Regular, Extra, и Puppy delite из трех ингредиентов K9, K8, и KI. Regular содержит 1/3 каждого из ингредиентов и дает прибыль $0,20 за банку. Extra содержит 50% K9 и по 25% каждого из ингредиентов K8 и K1 и дает прибыль $0,18 за банку. Puppy delite содержит 10 % K8, 90% KI и дает прибыль $0,25 за банку. Продукция идет в банках по 1 кг. Запасы ингредиентов на неделю - 1900 кг K9, и по 1000 кг K8 и К1. 1. Определите оптимальный план производства смесей Regular, Extra и Puppy, максимизирующий прибыль. 2. Все ли типы смесей выгодно производить? Что должно быть изменено, чтобы производство убыточной смеси стало выгодным? Можно ли изменить что-то в технологии или в ценовой политике так, чтобы все смеси стали выгодно производить? Попытайтесь сделать это. 3. Допустим, Вы можете купить дополнительные 500 кг одного из компонентов? Какой из ингредиентов (K9, K8 или KI) Вы предпочтете? Как увеличится прибыль? Подтвердите все ваши ответы вычислениями.
Фармацевтическая компания Фармацевтическая компания исследует возможность продвижения на рынок новой пищевой добавки, которая должна содержать микроэлементы: железо, кальций, фосфор. Добавка может быть получена путем смешивания 3 ингредиентов, которые компания обозначает как T5, N1 и T4. Количество трех микроэлементов (мг/на 100 мл), содержащихся в каждом из ингредиентов, минимальный и максимальный уровень каждого микроэлемента в 1.2-литровой бутылке и издержки на производство 100 мл каждого ингредиента приведены в таблице.
Менеджер хочет найти комбинацию ингредиентов в пищевой добавке, минимизирующую издержки на их производство. 1. Сформулируйте и решите задачу линейного программирования (ЛП). 2. Менеджер имеет предложение продать N1 компонент по 0.7р. за 100 мл. В этом случае новую пищевую добавку придется готовить только из смеси T5 и T4. Стоит ли принимать это предложение? Лабораторная работа №2 Транспортные задачи, логистика и задачи о назначениях |
|
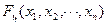линейно зависит от переменных решения 
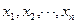и ограничения представляют собой линейные уравнения или неравенства относительно переменных решения.
