|
|
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИОПРЕДЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ С ПОМОЩЬЮ УНИВЕРСАЛЬНОГО МАЯТНИКА
ТРЕБОВАНИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ При выполнении работы соблюдать требования инструкции №170 по технике безопасности. При работе с электросекундомером соблюдайте правила безопасного обращения с прибором. При проведении эксперимента колебания маятников следует возбуждать не толчками, а малыми отклонениями (20 – 30) от положения равновесия. ЦЕЛЬ РАБОТЫ: опытное определение ускорения силы тяжести. ПРИБОРЫ И ОБОРУДОВАНИЕ: универсальный маятник, секундомер.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Ускорение силы тяжести является одной из важнейших характеристик гравитационного поля Земли. Его значения закладываются в технические расчеты практически всех крупных инженерных сооружений, особенно, высотных зданий, гидротехнических сооружений. Определения ускорения силы тяжести Используемая в лабораторной эксперименте установка – универсальный маятник представляет собой систему из двух маятников. Методика работы с ними несколько отлична, хотя и содержит много общих черт. Определение Колебание величины х называется гармоническим, если его изменение происходит по закону «синуса» или «косинуса»:
где х – мгновенное значение колеблющейся величины; А – амплитуда колебания; Классическими примерами колебательных движений являются колебания маятников с малой амплитудой. Ниже мы рассмотрим два вида колебаний: колебания математического и физического маятников.
МАТЕМАТИЧЕСКИЙ МАЯТНИК
Пусть
Знак минус возникает потому, что проекция силы противоположна направлению отклонения маятника. При малых отклонениях маятника от положения равновесия
Введем обозначение
Общим решением уравнения (3) можно считать функцию
Постоянные интегрирования А и
Из формулы (5) мы видим, что малые колебания маятника являются изохронными; их период не зависит от амплитуды и массы маятника. Именно это обстоятельство и позволяет использовать формулу (5) для определения ускорения силы тяжести. ФИЗИЧЕСКИЙ МАЯТНИК
Тело, совершающее колебания около неподвижной оси, не проходящей через его центр масс, называется физическим маятником. В данном случае тело совершает возвратно-вращательное движение. На рис.2 О след оси вращения на плоскости чертежа; ОО¢=
где
Для случая малых колебаний уравнение запишется в виде
где
Амплитуда колебаний
Здесь мы снова видим, что колебания маятника изохронны, таким образом, в принципе эти формулы можно использовать для определения ускорения силы тяжести.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ Универсальный маятник представляет собой прибор, соединяющий маятник, являющийся имитацией математического, и оборотный физический маятник. Строго говоря, в установке скомбинированы два физических маятника, однако условие, что длина нити, на которой подвешен шарик, много больше его размеров позволяет этот маятник принять за математический. В случае проведения эксперимента с математическим маятником возникает проблема с определением Для исключения возникающей значительной погрешности следует определить период колебаний Т1 при длине нити Из формулы (5) имеем: и Мы не знаем точных значений Обратим теперь внимание на особенность физического маятника. Он имеет две призмы для крепления на оси колебаний. Положения этих призм подбираются так, чтобы периоды колебаний относительно той и другой призм были равны (именно поэтому маятник и называют поворотным). Расстояние между точками крепления груза равно
где Для каждой из опор в отдельности имеем:
При Т1 = Т2 легко получаем
После подстановки (13) в (12) получаем:
где В состав лабораторной установки входит также секундомер. Обычная комплектация лабораторной работы включает в себя электрический секундомер, который может быть заменен и механическим секундомером. На лицевой панели электросекундомера расположены кнопки управления: включения и выключения прибора, установки нуля и кнопка запуска. Точность прибора 0,01 с.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 3.1 ОПРЕДЕЛЕНИЕ МАТЕМАТИЧЕСКОГО МАЯТНИКА 1. Задать длину нити подвеса 2. Отклонив маятник на 30–50 от положения равновесия, освободить его и определить время 3. Изменить длину 4. Выполнить опыты согласно п. 2 и результаты занести в таблицу 1. Результаты опытов с математическим маятником Таблица 1
Произвести расчет 5. Повторить п. 1-4 не менее 5 раз. Вычислить среднее значение 3.2 ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ |
|
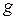 с высокой степенью точности является задачей специальной прикладной отрасли науки – гравиметрии. На основании значений
с высокой степенью точности является задачей специальной прикладной отрасли науки – гравиметрии. На основании значений  , или
, или  ,
,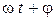 или
или  – фаза колебания;
– фаза колебания;  – циклическая частота;
– циклическая частота;  или
или  – начальная фаза колебаний;
– начальная фаза колебаний;  – текущий момент времени.
– текущий момент времени. Математическим маятником называют материальную точку, совершающую колебания на невесомой нерастяжимой нити. Естественно, что математический маятник – это физическая абстракция, физическая модель. Реальным образом ее может быть принят шарик малых размеров, подвешенный на достаточно длинной нити (рис.1).
Математическим маятником называют материальную точку, совершающую колебания на невесомой нерастяжимой нити. Естественно, что математический маятник – это физическая абстракция, физическая модель. Реальным образом ее может быть принят шарик малых размеров, подвешенный на достаточно длинной нити (рис.1). – длина нити маятника, т – его масса. Характеристиками, определяющими колебательное движение, можно считать или угол отклонения нити от равновесия
– длина нити маятника, т – его масса. Характеристиками, определяющими колебательное движение, можно считать или угол отклонения нити от равновесия  или же само отклонение х, отсчитываемое по траектории движения. Если пренебречь силами сопротивления движению, то на тело маятника действуют две силы: сила тяжести
или же само отклонение х, отсчитываемое по траектории движения. Если пренебречь силами сопротивления движению, то на тело маятника действуют две силы: сила тяжести  и натяжение нити
и натяжение нити  . В проекции на направление касательной
. В проекции на направление касательной  уравнение движения маятника запишется так:
уравнение движения маятника запишется так: (1)
(1)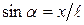 . Таким образом, уравнение движения (1) запишется в виде:
. Таким образом, уравнение движения (1) запишется в виде: . (2)
. (2) , имеем:
, имеем: . (3)
. (3) . (4)
. (4) определяются из начальных условий, тогда как циклическая частота колебательного движения маятника
определяются из начальных условий, тогда как циклическая частота колебательного движения маятника  . Вспомним, что период колебаний Т и их циклическая частота связаны соотношением
. Вспомним, что период колебаний Т и их циклическая частота связаны соотношением 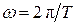 . Откуда следует, что период колебаний математического маятника
. Откуда следует, что период колебаний математического маятника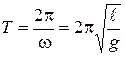 . (5)
. (5) Рис. 2
Рис. 2
 – расстояние от оси вращения до центра масс маятника. К телу приложены силы: тяжести
– расстояние от оси вращения до центра масс маятника. К телу приложены силы: тяжести  и реакции оси
и реакции оси  . Момент относительно оси вращения создает только сила
. Момент относительно оси вращения создает только сила  , (6)
, (6)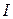 – момент инерции тела относительно оси колебания;
– момент инерции тела относительно оси колебания;  – угловое ускорение тела;
– угловое ускорение тела; 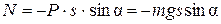 , знак «–» имеет то же объяснение, что и в случае математического маятника. После соответствующих подстановок приходим к уравнению движения в виде:
, знак «–» имеет то же объяснение, что и в случае математического маятника. После соответствующих подстановок приходим к уравнению движения в виде: . (7)
. (7) , (8)
, (8) . Решением данного дифференциального уравнения будет функция
. Решением данного дифференциального уравнения будет функция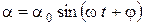 . (9)
. (9) и начальная фаза определяются начальными условиями, а вот частота и период колебаний Т определяются параметрами физического маятника
и начальная фаза определяются начальными условиями, а вот частота и период колебаний Т определяются параметрами физического маятника ;
;  . (10)
. (10) , измеренной от центра колебаний до точки крепления нити на шарике, ( т. е. задать некоторое неизвестное значение длины маятника
, измеренной от центра колебаний до точки крепления нити на шарике, ( т. е. задать некоторое неизвестное значение длины маятника  ), затем измерить период колебаний Т2 при длине нити
), затем измерить период колебаний Т2 при длине нити 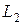 (длина маятника станет
(длина маятника станет  ).
). ;
; 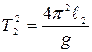 . Из последних выражений легко получить:
. Из последних выражений легко получить:  ,
, . (11)
. (11) . Разность
. Разность  можно определить с высокой степенью точности, и таким образом формула (11) будет расчетной для определения
можно определить с высокой степенью точности, и таким образом формула (11) будет расчетной для определения 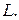 В его конструкции реализована следующая идея. По теореме Штейнера момент инерции относительно оси вращения, около которой совершаются колебания
В его конструкции реализована следующая идея. По теореме Штейнера момент инерции относительно оси вращения, около которой совершаются колебания ,
, – момент инерции маятника относительно центра масс,
– момент инерции маятника относительно центра масс,  расстояние от оси вращения (точки крепления маятника) до центра масс.
расстояние от оси вращения (точки крепления маятника) до центра масс. (12)
(12) . (13)
. (13) . Очевидно,
. Очевидно,  Тогда расчетная формула для
Тогда расчетная формула для  , (14)
, (14) – расстояние между точками подвеса оборотного маятника, которое может быть измерено достаточно точно.
– расстояние между точками подвеса оборотного маятника, которое может быть измерено достаточно точно. 20–30 полных колебаний. Опыт повторить не менее 5 раз. Результаты измерений занести в таблицу 1.
20–30 полных колебаний. Опыт повторить не менее 5 раз. Результаты измерений занести в таблицу 1.

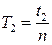
 .
.