Обратная связь
|
Метод определения длительности удара МЕХАНИЧЕСКИЙ УДАР
Нижний Новгород
2013 год
Лабораторная работа № 1-21
Механический удар
Цель работы: Ознакомиться с элементами теории механического удара и экспериментально определить время удара  , среднюю силу удара F, коэффициент восстановления Е, а также изучить основные характеристики удара и ознакомиться с цифровыми приборами для измерения временного интервалов. , среднюю силу удара F, коэффициент восстановления Е, а также изучить основные характеристики удара и ознакомиться с цифровыми приборами для измерения временного интервалов.
Теоретическая часть
 Ударом называется изменения состояния движения тела, вследствие кратковременного взаимодействия его с другим телом. Во время удара оба тела претерпевают изменения формы (деформацию). Сущность упругого удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел, за короткое время, преобразуется в энергию упругой деформации или в той или иной степени в энергию молекулярного движения. В процессе удара происходит перераспределение энергии между соударяющимися телами. Ударом называется изменения состояния движения тела, вследствие кратковременного взаимодействия его с другим телом. Во время удара оба тела претерпевают изменения формы (деформацию). Сущность упругого удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел, за короткое время, преобразуется в энергию упругой деформации или в той или иной степени в энергию молекулярного движения. В процессе удара происходит перераспределение энергии между соударяющимися телами.
рис.1
Пусть на плоскую поверхность массивной пластины падает шар с некоторой скоростью V1 и отскакивает от нее со скоростью V2.
Обозначим  – нормальные и тангенциальные составляющие скоростей – нормальные и тангенциальные составляющие скоростей  и и  , а , а  и и  – соответственно углы падения и отражения. В идеальном случае при абсолютно упругом ударе, нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны – соответственно углы падения и отражения. В идеальном случае при абсолютно упругом ударе, нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны  ; ;  . При ударе всегда происходит частичная потеря механической энергии. Отношение как нормальных, так и тангенциальных составляющих скорости после удара к составляющим скорости до удара есть физическая характеристика, зависящая от природы сталкивающихся тел. . При ударе всегда происходит частичная потеря механической энергии. Отношение как нормальных, так и тангенциальных составляющих скорости после удара к составляющим скорости до удара есть физическая характеристика, зависящая от природы сталкивающихся тел.
 (1) (1)
Эту характеристику Е называют коэффициентом восстановления. Числовое значение его лежит между 0 и 1.
Определение средней силы удара,
Начальной и конечной скоростей шарика при ударе
 Экспериментальная установка состоит из стального шарика А, подвешенного на проводящих нитях, и неподвижного тела В большей массы, с которым шарик соударяется. Угол отклонения подвеса α измеряется по шкале. В момент удара на шар массой m действует сила тяжести со стороны Земли Экспериментальная установка состоит из стального шарика А, подвешенного на проводящих нитях, и неподвижного тела В большей массы, с которым шарик соударяется. Угол отклонения подвеса α измеряется по шкале. В момент удара на шар массой m действует сила тяжести со стороны Земли  , сила реакции со стороны нити , сила реакции со стороны нити  и средняя сила удара и средняя сила удара 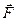 со стороны тела В (см. рис.2.). со стороны тела В (см. рис.2.).
На основании теоремы об изменении импульса материальной точки:
 (2) (2)
где  и и  – векторы скоростей шара до и после удара; τ – длительность удара. – векторы скоростей шара до и после удара; τ – длительность удара.
После проектирования уравнения (2) на горизонтальную ось определим среднюю силу удара:
 (3) (3)
Скорости шарика V1 и V2 определяются на основании закона сохранения и превращения энергии. Изменение механической энергии системы, образованной шариком и неподвижным телом В, в поле тяготения Земли определятся суммарной работой всех внешних и внутренних не потенциальных сил. Поскольку внешняя сила  перпендикулярна перемещению и нить нерастяжима, то эта сила работы не совершает, внешняя сила перпендикулярна перемещению и нить нерастяжима, то эта сила работы не совершает, внешняя сила  и внутренняя сила упругого взаимодействия и внутренняя сила упругого взаимодействия  – потенциальны. Если эти силы много больше других не потенциальных сил, то полная механическая энергия выбранной системы не меняется. Поэтому, уравнение баланса энергии можно записать в виде: – потенциальны. Если эти силы много больше других не потенциальных сил, то полная механическая энергия выбранной системы не меняется. Поэтому, уравнение баланса энергии можно записать в виде:
 (4) (4)
Из чертежа (рис. 2) следует, что  , тогда из уравнения (4) получим значения начальной V1 и конечной V2 скоростей шарика: , тогда из уравнения (4) получим значения начальной V1 и конечной V2 скоростей шарика:
 (5) (5)
где  и и 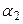 - углы отклонения шара до и после соударения. - углы отклонения шара до и после соударения.
Метод определения длительности удара
В данной работе длительность удара шарика о плиту определяется частотомером Ч3-54, функциональная схема которого представлена на рис.3. С генератора подается на вход системы управления СУ импульсы с периодом Т. Когда в процессе соударения металлической плиты В, электрическая цепь, образованная СУ, проводящими нитями подвеса шара, шаром, плитой В и счетчиком импульсов Сч, оказывается замкнутой, и система управления СУ пропускает на вход счетчика Сч импульсы электрического тока только в интервале времени  , равном времени длительности удара. Число импульсов, зарегистрированных за время , равном времени длительности удара. Число импульсов, зарегистрированных за время  , равно , равно  , откуда , откуда 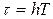 . .
Чтобы определить длительность удара  , необходимо число импульсов, зарегистрированных счетчиком, умножить на период импульсов, снимаемых с генератора Г. , необходимо число импульсов, зарегистрированных счетчиком, умножить на период импульсов, снимаемых с генератора Г.
Экспериментальная часть
Исходные данные:
1. Масса шарика m = (16,7 ± 0,1)*10-3 кг.
2. Длина нити l = 0,31 ± 0,01 м.
3. Ускорение свободного падения g = (9,81 ± 0,005) м/с2.
4. Опыт для каждого угла выполняем 5 раз.
Результаты опыта занесем в таблицу:
| №
| α1 = 200
| α1 = 300
| α1 = 400
| α1 = 500
| α1 = 600
|  i i
|  2i 2i
|  i i
|  2i 2i
|  i i
|  2i 2i
|  i i
|  2i 2i
|  i i
|  2i 2i
| |
| 61,9
| 17,1
| 58,0
| 26,8
| 54,9
| 37,0
| 52,4
| 43,6
| 48,9
| 57,8
| |
| 65,7
| 17,2
| 58,2
| 26,5
| 45,2
| 35,9
| 51,0
| 45,0
| 42,6
| 58,0
| |
| 64,0
| 16,9
| 58,4
| 26,9
| 52,8
| 36,7
| 49,9
| 46,7
| 49,6
| 57,2
| |
| 65,4
| 16,8
| 58,4
| 26,7
| 54,3
| 36,0
| 48,2
| 46,0
| 48,5
| 57,6
| |
| 64,0
| 16,9
| 57,3
| 26,8
| 52,4
| 37,0
| 50,2
| 43,9
| 48,4
| 58,1
| | Сред.
| 64,2
| 16,98
| 58,06
| 26,74
| 51,92
| 36,52
| 50,34
| 45,04
| 47,6
| 57,74
|
Расчёты
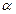 =200 =200  мкс мкс

 0,6054 м/с 0,6054 м/с
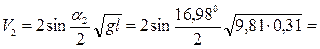 0,5148 м/с 0,5148 м/с


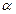 =300 =300  мкс мкс
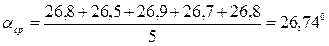
 0,9026 м/с 0,9026 м/с
 0,8064 м/с 0,8064 м/с


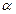 =400 =400  мкс мкс

 1,1928 м/с 1,1928 м/с
 1,0927 м/с 1,0927 м/с


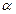 =500 =500  мкс мкс

 1,4739 м/с 1,4739 м/с
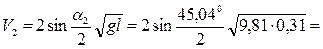 1,3357 м/с 1,3357 м/с

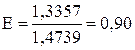
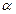 =600 =600  мкс мкс

 1,7438 м/с 1,7438 м/с
 1,6839 м/с 1,6839 м/с


 и и  –скорости шарика до и после удара. –скорости шарика до и после удара.
<  > – среднее значение силы удара. > – среднее значение силы удара.
< > – средняя длительность удара. > – средняя длительность удара.
Е – коэффициент восстановления.
Результаты расчетов

| <  >, Н >, Н
|  ,м/с ,м/с
|  ,м/с ,м/с
| <  >, мкс >, мкс
| Е
| 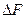 ,Н ,Н
|  ,м/с ,м/с
| 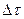 ,мкс ,мкс
| | 200
| 291,39
| 0,6054
| 0,5148
| 64,2
| 0,85
|
|
|
| | 300
| 491,56
| 0,9026
| 0,8064
| 58,6
| 0,89
| 200,17
| 0,2972
| 5,6
| | 400
| 735,12
| 1,1928
| 1,0927
| 51,92
| 0,91
|
|
|
| | 500
| 932,06
| 1,4739
| 1,3357
| 50,34
| 0,90
|
|
|
| | 600
| 1202,57
| 1,7438
| 1,6839
| 47,6
| 0,96
|
|
|
|
|
|
 , среднюю силу удара F, коэффициент восстановления Е, а также изучить основные характеристики удара и ознакомиться с цифровыми приборами для измерения временного интервалов.
, среднюю силу удара F, коэффициент восстановления Е, а также изучить основные характеристики удара и ознакомиться с цифровыми приборами для измерения временного интервалов. Ударом называется изменения состояния движения тела, вследствие кратковременного взаимодействия его с другим телом. Во время удара оба тела претерпевают изменения формы (деформацию). Сущность упругого удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел, за короткое время, преобразуется в энергию упругой деформации или в той или иной степени в энергию молекулярного движения. В процессе удара происходит перераспределение энергии между соударяющимися телами.
Ударом называется изменения состояния движения тела, вследствие кратковременного взаимодействия его с другим телом. Во время удара оба тела претерпевают изменения формы (деформацию). Сущность упругого удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел, за короткое время, преобразуется в энергию упругой деформации или в той или иной степени в энергию молекулярного движения. В процессе удара происходит перераспределение энергии между соударяющимися телами. – нормальные и тангенциальные составляющие скоростей
– нормальные и тангенциальные составляющие скоростей  и
и  , а
, а  и
и  – соответственно углы падения и отражения. В идеальном случае при абсолютно упругом ударе, нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны
– соответственно углы падения и отражения. В идеальном случае при абсолютно упругом ударе, нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны  ;
;  . При ударе всегда происходит частичная потеря механической энергии. Отношение как нормальных, так и тангенциальных составляющих скорости после удара к составляющим скорости до удара есть физическая характеристика, зависящая от природы сталкивающихся тел.
. При ударе всегда происходит частичная потеря механической энергии. Отношение как нормальных, так и тангенциальных составляющих скорости после удара к составляющим скорости до удара есть физическая характеристика, зависящая от природы сталкивающихся тел. (1)
(1) Экспериментальная установка состоит из стального шарика А, подвешенного на проводящих нитях, и неподвижного тела В большей массы, с которым шарик соударяется. Угол отклонения подвеса α измеряется по шкале. В момент удара на шар массой m действует сила тяжести со стороны Земли
Экспериментальная установка состоит из стального шарика А, подвешенного на проводящих нитях, и неподвижного тела В большей массы, с которым шарик соударяется. Угол отклонения подвеса α измеряется по шкале. В момент удара на шар массой m действует сила тяжести со стороны Земли  , сила реакции со стороны нити
, сила реакции со стороны нити  и средняя сила удара
и средняя сила удара 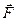 со стороны тела В (см. рис.2.).
со стороны тела В (см. рис.2.). (2)
(2) – векторы скоростей шара до и после удара; τ – длительность удара.
– векторы скоростей шара до и после удара; τ – длительность удара. (3)
(3) перпендикулярна перемещению и нить нерастяжима, то эта сила работы не совершает, внешняя сила
перпендикулярна перемещению и нить нерастяжима, то эта сила работы не совершает, внешняя сила  и внутренняя сила упругого взаимодействия
и внутренняя сила упругого взаимодействия  – потенциальны. Если эти силы много больше других не потенциальных сил, то полная механическая энергия выбранной системы не меняется. Поэтому, уравнение баланса энергии можно записать в виде:
– потенциальны. Если эти силы много больше других не потенциальных сил, то полная механическая энергия выбранной системы не меняется. Поэтому, уравнение баланса энергии можно записать в виде: (4)
(4) , тогда из уравнения (4) получим значения начальной V1 и конечной V2 скоростей шарика:
, тогда из уравнения (4) получим значения начальной V1 и конечной V2 скоростей шарика: (5)
(5) и
и 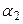 - углы отклонения шара до и после соударения.
- углы отклонения шара до и после соударения.
 , откуда
, откуда 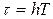 .
. 2i
2i
 =200
=200  мкс
мкс
 0,6054 м/с
0,6054 м/с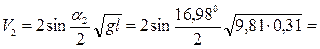 0,5148 м/с
0,5148 м/с

 мкс
мкс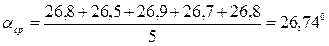
 0,9026 м/с
0,9026 м/с 0,8064 м/с
0,8064 м/с

 мкс
мкс
 1,1928 м/с
1,1928 м/с 1,0927 м/с
1,0927 м/с

 мкс
мкс
 1,4739 м/с
1,4739 м/с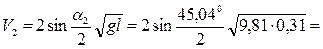 1,3357 м/с
1,3357 м/с
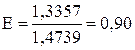
 мкс
мкс
 1,7438 м/с
1,7438 м/с 1,6839 м/с
1,6839 м/с

 и
и  –скорости шарика до и после удара.
–скорости шарика до и после удара. > – среднее значение силы удара.
> – среднее значение силы удара. > – средняя длительность удара.
> – средняя длительность удара.
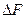 ,Н
,Н
 ,м/с
,м/с
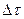 ,мкс
,мкс