|
|
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯЛАБОРАТОРНАЯ РАБОТА ВМ №4 ОПРЕДЕЛЕНИЕ КАЧЕСТВА ОБРАБОТКИ ПОВЕРХНОСТИ С ПОМОЩЬЮ МИКРОИНТЕРФЕРОМЕТРА
ТРЕБОВАНИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ Прибор МИИ-4 имеет подключение к электрической цепи через понижающий трансформатор 220/6 В. Не допускайте перегрева осветительного узла прибора. При работе соблюдайте требования инструкции по технике безопасности №170. Не включайте прибор, пока не ознакомитесь с его устройством. ЦЕЛЬ РАБОТЫ: Определение качества обработки поверхности по интерференционной картине, создаваемой интерферометром МИИ-4. ПРИБОРЫ И ОБОРУДОВАНИЕ: микроинтерферометр типа МИИ-4, понижающий трансформатор, исследуемый образец.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ В основе принципа действия прибора лежит явление интерференции света. Под интерференцией понимается явление стационарного (т.е. независящего от времени), перераспределения энергии в световом поле двух когерентных источников света при их наложении . Интерференция – явление, характерное для всех волновых процессов, и наблюдение интерференции у световых пучков наглядно свидетельствует о волновой природе света. Теория и опыт неопровержимо свидетельствуют, что свет представляет собой электромагнитные волны диапазона 0,40×10-6 – 0,76×10-6 метров. Электромагнитные волны – поперечные, характеризуются колебанием двух векторов: напряженности электрического поля
где Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями электрической составляющей поля волны, в связи с чем вводится понятие светового вектора, под которым понимается вектор электрической напряженности Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке колебания одинакового направления
где Е01, Е02 – амплитудные значения светового вектора, а величины
Результирующее колебание в общем случае определяется в соответствии с принципом суперпозиции. В нашем случае (колебания одинакового направления) удобно воспользоваться графическим методом векторного сложения амплитуд. Под вектором амплитуды понимается вектор Проекции векторов
а фаза
Как известно, интенсивность волны (в данном случае освещенность) пропорциональна квадрату амплитуды колебания, а в нашем случае
Таким образом, интенсивность светового поля будет пульсировать между крайними значениями с частотой
Вот откуда и следует известный закон фотометрии: освещенность от двух источников равна сумме освещенностей. Представляет интерес частный случай, когда
условия минимума
Числа k и т называют соответственно порядком максимума и порядком минимума. Излучение светящегося тела слагается из волн, испускаемых атомами тела. Излучение отдельного атома продолжается 10-8 с, за это время успевает образоваться цуг волн протяженностью ~3 м. Испустив свою избыточную энергию в виде излучения, атом возвращается в нормальное (невозбужденное) состояние. Спустя некоторый промежуток времени атом может опять возбудиться и начать излучать свет. Отдельный цуг волн обладает высокой степенью монохроматичности. Но в каждый момент времени излучение света осуществляется не одним, а весьма большим числом атомов светящегося тела. Эти атомы излучают световые волны независимо друг от друга, поэтому монохроматичность совокупного излучения источника света нарушается, начальные фазы тоже не связаны между собой; даже для одного и того же атома начальные фазы могут меняться. Значит, волны получаются некогерентными. Когерентные световые волны можно получить, разделив волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти различные пути, а потом наложить их друг на друга, наблюдается интерференционная картина. Практически это может быть осуществлено различными способами: с помощью зеркал, приз, экранов и т.д.Разность оптических путей, проходимых волнами, не должна быть очень большой, чтобы складываемые колебания принадлежали одному цугу волн.
Пусть разделение волн происходит в точке Р (рис.2). До точки Р первая волна проходит в среде с показателем преломления Если оптическая разность хода равна целому числу длин волн в вакууме,
то разность фаз Если
то В опыте Юнга (1802 г.) (рис.3) свет из точечного источника (малое отверстие, щель S) проходит через два равноудаленных отверстия – щели Рассмотрим результат наложения световых волн в некоторой точке М экрана, расположенного на некотором расстоянии параллельно
Проведем расчет интерференционной картины для линейных источников света, т.е. узких параллельных близко расположенных щелей. В этом случае на экране будет наблюдаться система чередующихся светлых и темных параллельных полос, как показано на рис.4. Рассмотрим две узких щели
Вычитая, имеем: Для получения различимой интерференционной картины должно быть
Подставив это значение D в условие максимума, имеем:
или Для минимумов интенсивности:
Величина
Как видим, Dх растет с уменьшением расстояния между источниками. Поэтому для того, чтобы картина интерференции была отчетливой, необходимо условие Если освещение производится белым светом (а он состоит из семи цветов, которые имеют разную длину волны), то интерференционная картина представляет чередование цветных полос, т.к. максимумы и минимумы разных цветов смещаются друг относительно друга. Ближе к центру расположены максимумы, соответствующие более коротким длинам волн – фиолетовым. В центре картины, при х = 0, максимумы всех длин волн совпадут, и центральная полоса будет белой. Интерференцию можно наблюдать не только в лабораторных условиях. Мы видим радужные окраски мыльных пленок, тонких пленок нефти, масла на поверхности воды. Эти явления обусловлены интерференцией, которая возникает в результате наложения когерентных волн, отражающихся от верхней поверхности пленки. Явление интерференции нашло практическое применение для определения длин волн световых лучей, для уменьшения отражения света на границах раздела линз в различных оптических системах (“просветление оптики”, в различных типах интерферометров). Подробнее рассмотрим интерферометр, применяемый для контроля за чистотой обработки металлических поверхностей с высоким классом точности.
12 |
|
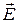 и магнитной индукции
и магнитной индукции 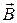 . Колебания электрической и магнитной составляющих поля световой волны происходят в одинаковых фазах во взаимно перпендикулярных плоскостях. Как показывает исследование, векторы
. Колебания электрической и магнитной составляющих поля световой волны происходят в одинаковых фазах во взаимно перпендикулярных плоскостях. Как показывает исследование, векторы  ,
, - расстояние, на которое распространилась волна от источника,
- расстояние, на которое распространилась волна от источника,  - скорость распространения волны.
- скорость распространения волны.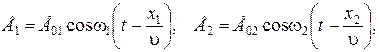
 и
и 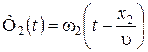 представляют собой фазы колебаний.
представляют собой фазы колебаний. Рис. 1.
Рис. 1.
 (см. рис.1).
(см. рис.1). и
и  на ось Х представляют собой складываемые состояния колебаний в данный момент времени, вектор
на ось Х представляют собой складываемые состояния колебаний в данный момент времени, вектор  представляет собой вектор амплитуды результирующего колебания, а угол
представляет собой вектор амплитуды результирующего колебания, а угол  – фазу результирующего колебания. С изменением времени
– фазу результирующего колебания. С изменением времени  векторы
векторы  будут меняться сложным образом, так что результирующее колебание не будет гармоническим. Амплитуда этого колебания определяется уравнением:
будут меняться сложным образом, так что результирующее колебание не будет гармоническим. Амплитуда этого колебания определяется уравнением: ,
, .
.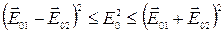 .
. ~1015 с-1. Ни глаз, ни оптический прибор не в состоянии фиксировать мгновенное состояние светового поля, измеряющегося с такой огромной частотой, а способно лишь фиксировать его среднее значение:
~1015 с-1. Ни глаз, ни оптический прибор не в состоянии фиксировать мгновенное состояние светового поля, измеряющегося с такой огромной частотой, а способно лишь фиксировать его среднее значение: .
. , и разность фаз
, и разность фаз  не зависит от времени и остается постоянной. Волны, удовлетворяющие этим условиям, называются когерентными. В световом поле когерентных источников света происходит стационарное (не зависящее от времени) перераспределение энергии, в результате которого в одних местах происходит усиление интенсивности (максимум интерференции), а в других ослабление интенсивности (минимум интенсивности). Условия максимума интерференции получаются из очевидных соображений
не зависит от времени и остается постоянной. Волны, удовлетворяющие этим условиям, называются когерентными. В световом поле когерентных источников света происходит стационарное (не зависящее от времени) перераспределение энергии, в результате которого в одних местах происходит усиление интенсивности (максимум интерференции), а в других ослабление интенсивности (минимум интенсивности). Условия максимума интерференции получаются из очевидных соображений ;
; .
. Рис. 2.
Рис. 2.
 путь
путь  , вторая волна – в среде с показателем преломления
, вторая волна – в среде с показателем преломления 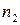 путь
путь  . Если в точке О фаза колебаний равна
. Если в точке О фаза колебаний равна  , то первая волна возбудит в точке Р колебание
, то первая волна возбудит в точке Р колебание  , а вторая волна – колебание
, а вторая волна – колебание  , где
, где  ,
,  - фазовые скорости волн. Разность фаз возбуждаемых в точке Р колебаний , равна
- фазовые скорости волн. Разность фаз возбуждаемых в точке Р колебаний , равна  Заменив
Заменив 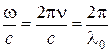 , где
, где  - длина волны в вакууме, имеем
- длина волны в вакууме, имеем 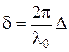 , где
, где 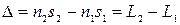 - оптическая разность хода.
- оптическая разность хода.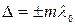 (т = 0,1,2….) , (1)
(т = 0,1,2….) , (1) Рис. 3. Схема опыта Юнга
Рис. 3. Схема опыта Юнга
 будет кратна 2π , и колебания, возбуждаемые в точке Р обеими волнами , будут происходить в одной фазе, т.е. (1) – условие максимума интерференции.
будет кратна 2π , и колебания, возбуждаемые в точке Р обеими волнами , будут происходить в одной фазе, т.е. (1) – условие максимума интерференции. равна полуцелому числу длин волн в вакууме,
равна полуцелому числу длин волн в вакууме, (т = 0,1,2….), (2)
(т = 0,1,2….), (2) , и колебания в точке Р будут в противофазе, т.е. (2) – условие минимума интерференции.
, и колебания в точке Р будут в противофазе, т.е. (2) – условие минимума интерференции. и
и  . Согласно принципу Гюйгенса, каждое малое отверстие
. Согласно принципу Гюйгенса, каждое малое отверстие  .
. Рис. 4. Схема расчета от интерференционной картины от двух линейных источников света
Рис. 4. Схема расчета от интерференционной картины от двух линейных источников света
 и
и  , расположенных перпендикулярно к плоскости чертежа на расстоянии
, расположенных перпендикулярно к плоскости чертежа на расстоянии  друг от друга. Экран тоже перпендикулярен плоскости чертежа и находится на расстоянии
друг от друга. Экран тоже перпендикулярен плоскости чертежа и находится на расстоянии  от щелей.. Рассчитаем разность хода до точки М, находящейся на расстоянии х от центральной линии экрана, относительно которой симметричны источники
от щелей.. Рассчитаем разность хода до точки М, находящейся на расстоянии х от центральной линии экрана, относительно которой симметричны источники 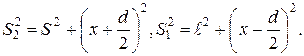
 .
. (это будет показано ниже). Отсюда следует, что
(это будет показано ниже). Отсюда следует, что  , очевидно,
, очевидно,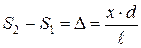 .
. ,
, .По этой формуле можно подсчитать положения последовательных максимумов.
.По этой формуле можно подсчитать положения последовательных максимумов.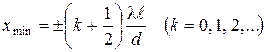 .
.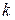 называется порядком интерференционного максимума или минимума. Расстояние между соседними максимумами или минимумами называется шириной интерференционной полосы и остается неизменной вдоль экрана
называется порядком интерференционного максимума или минимума. Расстояние между соседними максимумами или минимумами называется шириной интерференционной полосы и остается неизменной вдоль экрана  для данной длины волны:
для данной длины волны: .
. . Ширина полоски зависит от длины волны (
. Ширина полоски зависит от длины волны ( 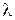 ). Если источник испускает монохроматический свет
). Если источник испускает монохроматический свет  , то интерференционная картина представляет собой чередование темных и светлых полос.
, то интерференционная картина представляет собой чередование темных и светлых полос.