|
|
Симплексные методы решения задач оптимизации в электроэнергетикеСимплексный метод относится к линейному программированию и применяется при решении задач оптимизации при наличии выпуклой целевой функции
и линейных уравнений-ограничений в форме неравенств
или же в матричной форме
Например, при наличии двух оптимизируемых параметров и четырех уравнений ограничений исходная модель имеет вид
Для решения задачи симплексным методом исходная модель приводится к стандартной, канонической форме. Для этого целевая функция и все уравнения-ограничения приводятся к форме равенств с неотрицательной правой частью. При этом все переменные также неотрицательны
Здесь Si – вспомогательная переменная, вводимая в i-е уравнение для приведения его к форме равенства, ее знак положителен для неравенств вида В канонической форме для данного примера число ограничений m=4, а число переменных увеличивается до n=6.
Рис. 53. Допустимое пространство решений
Допустимое пространство решений в координатах оптимизируемых параметров получается как пересечение прямых, уравнения которых получены приравниванием нулю вспомогательной переменной в одном из ограничений (см. рис. 53). Например, уравнение прямой, полученной приравниванием нулю вспомогательной переменной в первом ограничении S1=0 и проходящей через точки E и F, имеет вид
Точки A, B, C, D, E, F – экстремальные точки допустимого пространства решений, в которых обнуляются n–m переменных. Суть симплексного метода заключается в том, что оптимальное решение ищется среди экстремальных точек допустимого пространства решений по определенному алгоритму, уменьшающему число переборов. Например (см. рис. 54), если начальное приближение – точка A, то затем переход осуществляется к смежной точке, но не произвольной, а к той, которая обеспечивает наискорейший рост целевой функции.
Рис. 54. Геометрическая интерпретация симплексного метода
Симплексный метод включает следующие этапы: 1. составление начального базисного решения приравниванием нулю оптимизируемых параметров (в данном примере X1 и X2 и исходный базис при этом – S1, S2, S3, S4, см. табл. 3);
Табл. 3. Начальное базисное решение
2. определение включаемой в новый базис перемененной из числа небазисных переменных по максимальному по модулю отрицательному коэффициенту в z-строке (что соответствует наискорейшему росту целевой функции) или по наибольшему положительному при решении задачи максимизации (столбец, соответствующий включаемой переменной, является ведущим столбцом k); 3. определение исключаемой из базиса переменной по наименьшему положительному отношению правой части соответствующего ограничения к элементу ведущего столбца bi/aik (строка, соответствующая исключаемой переменной, является ведущей строкой r, Элемент на пересечении ведущей строки и ведущего столбца является ведущим элементом ark); 4. составление нового базисного решения (применительно к рассматриваемому примеру - см. табл. 4), в котором место исключаемой переменной в новом базисе занимает включаемая, все коэффициенты симплекс-таблицы пересчитываются по алгоритму Жордана- Гаусса
Табл. 4. Новое базисное решение
Метод искусственного базиса
Данный метод применяется в тех случаях, когда в системе имеются ограничения со знаками ≤, ≥, = и является модификацией ранее рассмотренного табличного симплексного метода. Решение производится путем введения в целевую функцию и ограничения искусственных переменных со знаками, зависящими от типа оптимума. Для исключения искусственных переменных из базиса они вводятся в целевую функцию с большими отрицательными коэффициентами –М или с большими положительными при решении задачи минимизации. Если в базисе отсутствуют искусственные переменные (все искусственные переменные исключены из базиса), то решение признается оптимальным. Исходная модель включает целевую функцию
и систему ограничений, включающую m ограничений-неравенств
и k ограничений-равенств
В качестве примера подобной исходной модели, включающей ограничения, как в форме равенств, так и в форме неравенств, можно рассмотреть минимизацию целевой функции z расходов при строительстве энергосистемы
В этой модели имеют место n ограничений неравенств по максимальной мощности электростанций и два ограничения равенства из условий мгновенного и долгосрочного баланса мощностей
где En – нормативный коэффициент эффективности капиталовложений в энергетике, K0i – капитальные вложения на единицу установленной мощности для i-й электростанции, [руб/МВт], Piуст – установленная мощность i-й электростанции, [МВт], Tmaxi – время использования максимальной мощности i-й электростанции, [час], γi – стоимость топлива для выработки электроэнергии для i-й электростанции, [руб/ кВт*ч], Pimax – максимальная мощность i-й электростанции, [МВт], Pн – мощность нагрузки, [МВт].
Алгоритм метода искусственного базиса включает следующие этапы: 1. введение в ограничения-неравенства вспомогательных переменных Xn+1….Xn+m для приведения ограничений к канонической форме; 2. введение в целевую функцию и все ограничения m+k искусственных переменных Xn+m+1….Xn+2m+k, в процессе которого модель приобретает вид
;
3. составление начального базисного решения (см. табл. 5), Табл. 5. Начальное базисное решение
где
4. определение включаемой в новый базис перемененной из числа небазисных переменных по максимальному по модулю отрицательному коэффициенту в z-строке искусственной целевой функции (столбец, соответствующий включаемой переменной, является ведущим столбцом k); 5. определение исключаемой из базиса переменная по наименьшему положительному отношению правой части соответствующего ограничения к элементу ведущего столбца bi/aik. (строка, соответствующая исключаемой переменной, является ведущей строкой r, элемент на пересечении ведущей строки и ведущего столбца является ведущим элементом ark); 6. составление нового базисного решения, в котором столбец, соответствующий исключаемой переменной удаляется из таблицы, место исключаемой переменой в базисе занимает включаемая переменная, позиция на пересечении ведущей строки и столбца Cб заполняется коэффициентом включаемой переменной в целевой функции, все коэффициенты симплекс-таблицы пересчитываются по алгоритму Жордана- Гаусса
Этот алгоритм повторяется до тех пор, пока из базиса не будут удалены все искусственные переменные.
Модифицированный симплексный метод В основу данного метода положены такие свойства линейной алгебры, которые позволяют в ходе решения задачи работать только с частью матрицы ограничений. Данный метод также называется методом обратной матрицы. В процессе работы алгоритма происходит спонтанное обращение матрицы ограничений по частям, соответствующим текущему базисному вектору. Это делает привлекательной машинную реализацию данного алгоритма вследствие экономии памяти под промежуточные переменные и сокращении времени вычислений. Использование данного метода особенно эффективно при n>>m. Общие и отличительные черты модифицированного симлексного метода относительно ранее рассмотренных показаны в табл. 6. Табл. 6. Традиционные и отличительные черты модифицированного симплексного метода
|
|
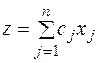



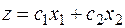


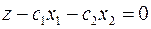

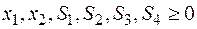 .
. и отрицательный для неравенств вида
и отрицательный для неравенств вида  .
.



 если i=r (т.е. для элементов ведущей строки),
если i=r (т.е. для элементов ведущей строки), если i≠r (т.е. для всех остальных элементов).
если i≠r (т.е. для всех остальных элементов).





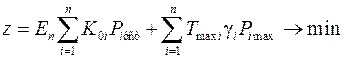 .
. ,
,


 ;
;