|
|
Внутренние силовые факторы. Основные определения и формулыУтверждено на заседании кафедры сопротивления материалов 28.02. 2012 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению расчетно-графической работы по сопротивлению материалов «ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ»
для бакалавров и специалистов
Ростов-на-Дону УДК 620.178.32 (076.5)
Методические указания по выполнению расчетно-графической работы по сопротивлению материалов «Построение эпюр внутренних силовых факторов». – Ростов н/Д: Рост. гос. строит. ун-т, 2012. – 24 с.
Содержат основные теоретические положения, примеры и порядок выполнения студентами расчетно-графической работы по сопротивлению материалов. Рассчитаны на студентов очного обучения.
УДК 620.178.32 (076.5)
Составители: канд. техн. наук, доц. Е.Э. Кадомцева канд. физ.-мат. наук, доц. Г.П. Стрельников
Редактор Н.Е. Гладких Темплан 2012г., поз. 88 Подписано в печать 4.06.12 Формат 60х84/16. Бумага писчая. Ризограф. Уч.-изд.л. 1,4. Тираж 200 экз. Заказ
Редакционно-издательский центр Ростовского государственного строительного университета. 344022, Ростов-на-Дону, Социалистическая, 162.
строительный университет, 2012
Основные типы балок и опорных связей
Балка соединяется с основанием при помощи опорных связей (опор). Существует несколько типов опор.
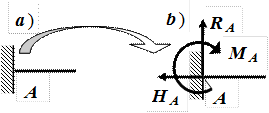
Шарнирно-неподвижная опора― рис. 1а
Рис. 1
Эта опора не позволяет сечению балки в точке А перемещаться в горизонтальном и вертикальном направлении, но при этом возможен поворот сечения в одной плоскости относительно оси цилиндрического шарнира. Поэтому в такой опоре возникает две реакции RA и HA (рис.1б).
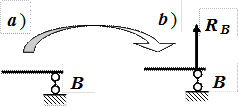
Шарнирно-подвижная опора― рис. 2а
Рис. 2
Эта опора допускает как поворот, так и перемещение сечения B по горизонтали. В такой опоре возникает только реакция RB (рис. 2б). Защемление или заделка― рис. 3а
Рис. 3
Опора не позволяет перемещений по двум направлениям и поворота сечения, близлежащего к опоре. В защемлении возникают следующие реакции: вертикальная сила RA, горизонтальная сила HA и момент MA (рис.3б). Для того чтобы балка работала, т.е. могла сопротивляться приложенным силам, необходимо ее закрепить. Наименьшее число связей, не позволяющих балке перемещаться в плоскости действия нагрузок, равно трем. Такие балки называются статически определимыми. Рассмотрим различные типы статически определимых балок, в зависимости от их опирания: консольная или жестко защемленная балка(рис.4a), балка на двух опорах ( однопролетная балка) с левой свисающей консолью(рис.4b) и балка с промежуточным шарниром(рис.4с).
a) b) c)
Рис. 4
Определение опорных реакций Для определения опорных реакций для плоской системы сил можно в общем случае составить три уравнения равновесия: S Fx =0. ― Сумма проекций всех сил на ось x равна нулю. S MA =0. ― Сумма моментов всех сил относительно точки A равна нулю. S MB=0. ― Сумма моментов всех сил относительно точки B равна нулю.
Составляя уравнения равновесия,обычно используют правило знаков, показанное на рис.5, т.е. горизонтальные и вертикальные силы положительны, если их направления совпадают с направлениями осей x и z. Положительное направление моментов ― против хода часовой стрелки. Рис. 5 Уравнение равновесия нужно стараться составлять так, чтобы в каждое уравнение входила только одна опорная реакция. Это облегчает нахождение опорных реакций. Внутренние силовые факторы. Основные определения и формулы В поперечном сечении балки или плоской рамы возникают следующие внутренние силовые факторы: продольная сила(N) ,поперечная силы (Q) и изгибающий момент (M). Положительные направления этих силовых факторов показано на рис.6. Продольная сила(N) считается положительной, если она вызывает растяжение рассматриваемой части балки (рамы); поперечная сила (Q) Рис.6
Внутренние силовые факторы определяются через внешние силы. Продольная сила (N) – это внутренняя сила, численно равная алгебраической сумме всех внешних сил, действующих по одну сторону от сечения параллельно оси балки. Поперечная сила (Q) – это внутренняя сила, численно равная алгебраической сумме всех внешних сил, действующих по одну сторону от сечения перпендикулярно оси балки. Изгибающий момент (M) –это внутренний момент, численно равный алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения относительно центра тяжести поперечного сечения (можно говорить относительно оси, проходящей через центр тяжести сечения и перпендикулярной плоскости действия сил). Правило знаков (рис.7). Продольная сила в поперечном сечении балки положительная(N= + Fxвнеш), если внешняя сила (Fxвнеш) направлена влево слева от сечения, а справа от сечения – вправо. Поперечная сила в поперечном сечении балки положительная Изгибающий момент в поперечном сечении балбалки положителен(M =+ Mвнеш), если момент внешней силы (Mвнеш) направлен походу часовой стрелки слева от сечения, а справа от сечения– против хода часовой стрелки. Рис.7
Продольная, поперечная сила и изгибающий момент отрицательны, если направления внешних сил и моментов внешних сил противоположны направлениям, указанным на рис.7. В ходе решения задач, приведенных ниже, будет показан фрагмент правила знаков, когда будем составлять выражения для продольных сил, поперечных сил и изгибающих моментов.
Эпюры и правила их построения
При расчетах на прочность очень важно знать распределение усилий по длине балки. Для этого строятся графики распределения усилий по длине балки, так называемые эпюры. Рассмотрим правила построения эпюр.
1. Определяем опорные реакции.
2. Разбиваем расчетную схему балки на участки. Границами участка являются точки приложения сосредоточенных сил, сосредоточенных моментов, точки начала и конца распределенной нагрузки.
3. Используя метод сечений, проводим поперечное сечение в пределах рассматриваемого участка, которое разбивает балку (раму) на две части. Выбираем левую или правую от сечения часть балки (рамы). Для определения внутренних усилий в сечении совершенно безразлично, какую часть рассматривать, левую или правую. Величины внутренних усилий будут одни и те же.
4. Составляем выражения для продольной силы, поперечной силы и изгибающего момента с учетом правила знаков.
5. Определяем значения продольных сил, поперечных сил и изгибающих моментов на границах участка. Если функциональная зависимость указанных силовых факторов нелинейная, вычисление производим еще и в промежуточной точке, например, где функция достигает экстремального значения.
6. Используя полученные значения продольных сил, поперечных сил и изгибающих моментов строим графики внутренних усилий. График каждого внутреннего усилия строится на отдельной линии, параллельной оси балки, и располагаются они непосредственно под балкой. Положительные значения продольных сил(N ) и поперечных сил(Q ) откладываются вверх, положительные значения изгибающих моментов(M ) откладываются вниз, т.к. эпюра M строится на растянутом волокне. Поле между графиком и нулевой линией (ось x) заштриховывается. На поле ставится знак внутреннего усилия в кружочке.
Исходные данные: а=2 м; b=3 м; F=4 кН; q1=6 кН/м; q2=5кН/м; m=9 кНм. Рис.8 Для заданной расчетной схемы консольной балки (рис.8) требуется: 1. Определить опорные реакции. 2. Построить эпюры поперечных сил (Q) и изгибающих моментов(M).
Решение Определение опорных реакций
Рис.9
Действие распределенных нагрузок q1и q2 заменим их равнодействующими: Rq1= q1·2м= 6 кН/м·2м=12кН; Rq2= q2·3м= 5 кН/м·3м=15кН.
Сумма проекций всех сил на ось x равна нулю: S Fx=0: HA= 0.
Сумма моментов всех сил относительно точки A равна нулю: S MA =0: –F·5м +Rq1(1м+3м) – m - Rq2·1,5м + MA=0; – 4кН·5м + 12кН·4м – 9кНм - 15кН ·1,5м + MA=0; - 3,5кНм + MA=0; MA=3,5кНм. Сумма моментов всех сил относительно точки Bравна нулю: S MB=0: –Rq1·1м – m + Rq2 (2м + 1,5м) + MA +RA (2м + 3м)=0;
–12кН·1м – 9кНм + 15кН ·3,5м + 3,5кНм +RA ·5м=0; 35кНм + RA ·5м =0; RA = Проверяем правильность вычисления опорных реакций (сумма проекций всех сил на вертикальную ось z должна быть равна 0)
S Fz = F– Rq1 + Rq2+ RA = 4кН – 12кН + 15кН + ( – 7кН)=19кН –19кН = 0. 2. Построение эпюр поперечных сил Q и изгибающих моментов M
Проводим сечение на I участке и рассматриваем левую от сечения часть балки (рис.10), т.к. слева от сечения сил приложено меньше, чем справа.
Рис.10
Q(x1) = F – q1 x1= 4кН– 6кН/м·x1;
Слева от сечения силаF направлена вверх, поэтому положительна, а сила q1 x1 (равнодействующая распределенной нагрузки на участке длинной x1) направлена вниз, поэтому отрицательна. Поперечная сила является линейной функцией координаты x1. Для построения ее графика определяем значение поперечной силы на границах участка.
Q (0) = 4кН– 6кН/м·0= 4кН (значение на левой границе участка); Q (2м) = 4кН– 6кН/м·2м= – 8кН (значение на правой границе участка). Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль: Q(x0) = 4кН– 6кН/м·x0=0; x0=
Переходим к определению изгибающего момента на Iучастке
Слева от сечения моменты всех сил берем относительно точки С1(центр тяжести поперечного сечения – рис.10). Момент силы F (плечо силы – x1) направлен по часовой стрелке, поэтому положительный, а момент силы q1 x1 (плечо силы – x1/2) направлен против хода часовой стрелке, поэтому отрицательный. Изгибающий момент (M) является квадратичной функцией координаты x1. Для построения его графика определяем значение изгибающего моментана границах участка и в найденной выше точке. M (0) = 4кН·0– 3кН/м· M (0,667м) = 4кН·0,667м– 3кН/м·(0,667м )2=1,33кНм; M (2м) = 4кН·2м– 3кН/м· (2м )2 = – 4 кНм (значение на правой границе участка). Проводим сечение на II участке и рассматриваем правую от сечения часть балки (рис.10).
Q(x2) = – RA – q2 x2= – (–7кН) – 5кН/м·x2 = 7кН– 5кН/м·x2; Положительное направление силы справа от сечения – вниз. Поперечная сила является линейной функцией координаты x2. Для построения ее графика определяем значение поперечной силы на границах участка.
Q(0) = 7кН– 5кН/м·0 = 7кН (значение на правой границе участка); Q(3м) = 7кН– 5кН/м·3м = – 8кН (значение на левой границе участка); Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль: Q(x0) = 7кН– 5кН/м·x0=0; x0= Переходим к определению изгибающего момента на IIучастке
= 3,5кНм –7кН·x2+2,5кН/м· Справа от сечения моменты всех сил, взятые относительно точки С2(центр тяжести поперечного сечения – рис.10), направлены против хода часовой стрелки, поэтому положительные. Изгибающий момент (M) является квадратичной функцией координаты x2. Для построения его графика определяем значение изгибающего моментана границах участка и в найденной выше точке.
M (0) = 3,5кНм –7кН·0+2,5кН/м·02=3,5кНм (значение на правой границе уч-ка); M (1,4м) = 3,5кНм –7кН·1,4м+2,5кН/м·(1,4м) 2 = –1,4 кНм; M (3м) = 3,5кНм –7кН·3м +2,5кН/м·(3м) 2 = 5 кНм (значение на левой границе участка).
Используя полученные значения, строим в масштабе эпюры поперечных сил и изгибающих моментов, как показано на рис.10.
Замечание. Здесь и в дальнейшем численные значения, полученные в ходе расчета, округляем до 3 значащих цифр.
|
|
 С Ростовский государственный
С Ростовский государственный


 считается положительной, если она стремится повернуть рассматриваемую часть балки (рамы) по ходу часовой стрелки; изгибающий момент (M) считается положительным, если он вызывает растяжение нижних волокон.
считается положительной, если она стремится повернуть рассматриваемую часть балки (рамы) по ходу часовой стрелки; изгибающий момент (M) считается положительным, если он вызывает растяжение нижних волокон. (Q= + Fzвнеш), если внешняя сила (Fzвнеш) направлена вверх слева от сечения, а справа от сечения– вниз.
(Q= + Fzвнеш), если внешняя сила (Fzвнеш) направлена вверх слева от сечения, а справа от сечения– вниз. Задача 1. Построение эпюр внутренних силовых факторов в консольной балке
Задача 1. Построение эпюр внутренних силовых факторов в консольной балке
 –7 кН.
–7 кН.
 I участок
I участок  (начало отсчета на левом конце балки);
(начало отсчета на левом конце балки); 0,666666 м=0,667 м;
0,666666 м=0,667 м; M(x1)= Fx1 –
M(x1)= Fx1 –  =4кН·x1– 6кН/м·
=4кН·x1– 6кН/м·  =4кН·x1– 3кН/м·
=4кН·x1– 3кН/м· 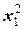
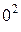 =0 (значение на левой границе участка);
=0 (значение на левой границе участка); II участок
II участок  (начало отсчета на правой границе участка);
(начало отсчета на правой границе участка); 1,4 м;
1,4 м; M (x2) = MA + RAx2+
M (x2) = MA + RAx2+  = 3,5кНм + (–7кН)·x2+5кН/м·
= 3,5кНм + (–7кН)·x2+5кН/м·  =
= ;
;