|
|
Построение эпюр внутренних усилийРасчет статически определимых элементарных расчетных схем на прочность Однопролетная балка Для заданной расчетной схемы балки требуется: 1.1.1. Провести полный кинематический анализ заданной расчетной схемы. 1.1.2. Определить опорные реакции для заданной расчетной схемы. 1.1.3. Построить эпюры изгибающих моментов и поперечных сил. Пример выполнения задания.Дано: расчетная схема балки (рис. 1.1.1); Рис. 1.1.1 Решение Проведение кинематического анализа заданной расчетной схемы Количественный кинематический анализ. Для проведения полного кинематического анализа необходимо заменить опорные связи их шарнирно-стержневым аналогом и обозначить эти сечения (см. рис. 1.1.2).
Рис. 1.1.2 Определим степень статической неопределимости заданной расчетной схемы (ЗРС) по формуле:
ü число жестких дисков системы: ü число простых шарниров, объединяющих жесткие диски системы: ü число опорных стержней: Имеем,
следовательно ЗРС статически определима. Качественный кинематический анализ. Проведем анализ ЗРС на геометрическую неизменяемость, которая обеспечивается наличием шарнирно-стержневого треугольника (ШСТ), образованного опорными связями, наложенными на диск (рис. 1.1.3).
Рис. 1.1.3 Таким образом, ЗРС геометрически неизменяема. Определение опорных реакций для заданной расчетной схемы На рис. 1.1.4 введем систему координат, оси которой определяют правило знаков для опорных реакций, заданных своими обозначениями, при этом неизвестные реакции считаются положительно направленными.
Рис. 1.1.4 Назначим уравнения равновесия для определения опорных реакций, причем для исключения взаимовлияния получаемых результатов выберем такие уравнения, из которых однозначно определялась бы каждая из исследуемых реакций и, не учитывалось влияние двух других, а именно:
Найдем опорные реакции, решив приведенные выше уравнения:
Знак “–“ перед числовым значением опорной реакции указывает на то, что направление данной реакции надо изменить на противоположное.
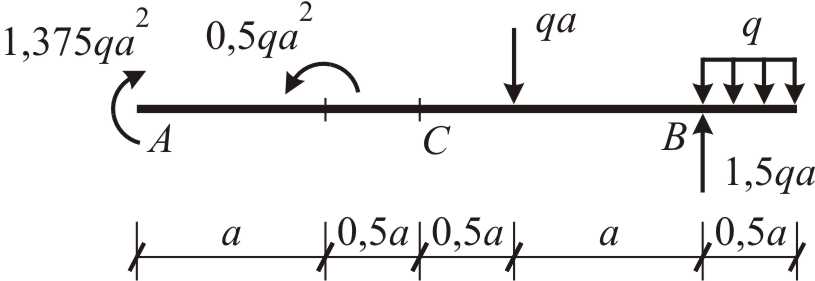
Рис. 1.1.5 Таким образом, реакции опорных связей определены, что позволяет указать на расчетной схеме все нагрузки в явном виде («в значениях»), см. рис. 1.1.5. Данные этого рисунка используются для проведения контроля правильности определения реакций опорных связей по ранее незадействованному уравнению Контроль: Построение эпюр внутренних усилий При плоском изгибе в поперечных сечениях балки возникают два внутренних силовых фактора (усилия): изгибающий момент M и поперечная сила Q. Для того чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента Mmax и положение сечения, в котором он возникает. Точно также надо знать наибольшую поперечную силу Qmax. В связи с этим возникает необходимость выяснить закон изменения M и Q по длине балки. Для этой цели обычно строят так называемые эпюры усилий. Эпюры усилий – графики распределения внутренних сил (усилий), построенные на осях расчетной схемы. Построение эпюр позволяет повысить наглядность картины распределения усилий по сечениям расчетной схемы от воздействия заданной нагрузки и определить сечения с максимальными значениями усилий. Для построения эпюр, используя метод сечений, определяют численные значения моментов и поперечных сил для ряда точек (контролируемых сечений) и по ним строят соответствующие графики. Назначение контролируемых сечений. Использование понятия контролируемого сечения позволяет разбить расчетную схему на участки, в пределах которых характер изменения усилия предопределен (см. Приложение 1). В балочных системах определяющим усилием является изгибающий момент, поскольку, имея эпюру моментов и расчетную схему, можно без сложных построений получить эпюру поперечных сил (см. Приложения 3, 4). Поэтому при назначении контролируемых сечений выделяем и нумеруем те сечения, в которых возникают характерные значения изгибающего момента M. К ним относятся: ü сечение по концам расчетной схемы; ü сечение, в точке приложения сосредоточенной силы (внешняя сила или опорная реакция); ü два сечения до и после точки приложения внешнего изгибающего момента; ü три сечения по концам и посередине участка действия распределенной нагрузки, свободной от сосредоточенной силы или изгибающего момента. В данном примере необходимо назначить семь контролируемых сечений (см. рис. 1.1.6). При этом согласно Приложения 3 будем иметь три участка с линейным изменением изгибающего момента (1–2, 3–4, 4–5) и один участок с параболическим законом (5–6–7).
Рис. 1.1.6 Вычисление ординат эпюры изгибающих моментов. Для определения численных значений усилия M в каждом контролируемом сечении применяется метод сечений, основанный на расчленении расчетной схемы по контролируемому сечению на две части. При этом формулируются условия равновесия только одной из частей с заменой отброшенной части на систему неизвестных усилий, передаваемых через плоскости разреза. Неизвестные усилия M и Q в контролируемых сечениях изображаются положительно направленными: · положительная поперечная сила Q стремится повернуть рассматриваемую часть балки по часовой стрелке (см. рис. 1.1.7); Правило знаков для поперечной силы Q
Рис. 1.1.7 · для изгибающего момента знак не ставят, важно, какие волокна этот момент растягивает.
Рис. 1.1.8
При использовании обозначения для искомого усилия вводится нумерация усилия двумя цифрами: Ø первая цифра – номер контролируемого сечения, в котором усилие определяется; Ø вторая цифра – номер сечения на противоположном конце рассматриваемого участка. Если в результате решения уравнения равновесия усилие M имеет отрицательный знак (рис. 1.1.9,а-г), то значит, изгибающий момент действует в противоположном направлении. Однако знак изгибающего момента не играет никакой роли, а вместо него вводится понятие «растянутое волокно поперечного сечения» (см. рис. 1.1.8). Вычислим значения изгибающих моментов в каждом из 7-ми назначенных контролируемых сечений, используя уравнения равновесия в моментах относительно точек расчленения расчетной схемы (рис. 1.1.9).
Рис. 1.1.9 (окончание)
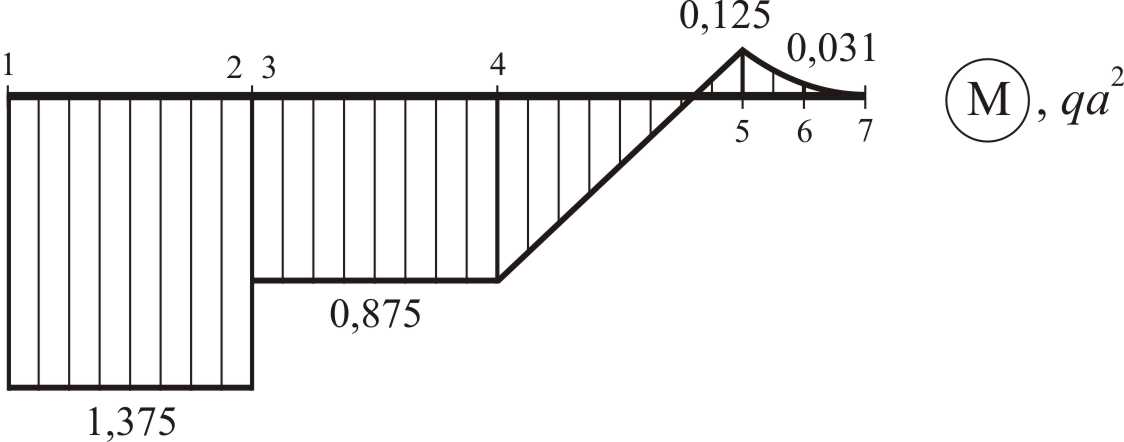
Построение эпюры изгибающих моментов. При построении эпюры изгибающих моментов необходимо: · отложить на осях расчетной схемы в контролируемых сечениях ординаты, равные найденным значениям моментов, со стороны растянутых волокон; · соединить ординаты, учитывая характер изменения усилия (линейный или параболический), см. Приложение 3. По данным рис. 9 построим эпюру изгибающих моментов (см. рис. 1.1.10).
Рис. 1.1.10
Вычисление ординат эпюры поперечных сил. Поперечная сила имеет геометрический смысл тангенса угла наклона касательной к эпюре изгибающего момента в рассматриваемом сечении и осью X балки. Поэтому вычисление ординат эпюры поперечных сил включает в себя: · расчленение эпюры изгибающих моментов на участки, в пределах которых момент изменяется по единому закону (линейному или параболическому); · вычисление для линейного участка эпюры изгибающих моментов модуля тангенса соответствующего угла (см. Приложение 4); · разложение криволинейного (параболического) участка эпюры изгибающих моментов на линейную и параболическую части и вычисление модулей тангенсов соответствующих углов (см. Приложение 4); · присвоение «инженерного» знака этим значениям: поперечная сила в сечении положительна, если участок с этим сечением на эпюре моментов нужно вращать по часовой стрелке для совмещения его оси с касательной на эпюре моментов (в этом же сечении), используя минимальный из углов поворота.
Рис. 1.1.11 Построение эпюры поперечных сил. При построении эпюры поперечных сил необходимо: · отложить на осях расчетной схемы в контролируемых сечениях ординаты, найденные по эпюре изгибающих моментов, причем положительные ординаты откладываются вверх от оси расчетной схемы, а отрицательные – вниз; · соединить ординаты, учитывая характер изменения усилия, см Приложение 1. По данным рис. 1.1.11 построим эпюру поперечных сил (см. рис. 1.1.12).
Рис. 1.1.12
Контроль правильности определения ординат эпюр усилий. Контроль правильности определения ординат эпюр усилий для ЗРС производится для произвольной части балки (рис. 1.1.13), для которой составляются уравнения равновесия (
Рис. 1.1.13 Уравнения равновесия отрезанной части ЗРС удовлетворяются тождественно, что свидетельствует о значительной достоверности проведенных построений. Кроме этого правильность построения эпюризгибающих моментов M и поперечных сил Q по характерным сечениям можно проверить, используя ряд общих правил. Одни из них являются следствиями из дифференциальных зависимостей между q, Q и M, другие вытекают непосредственно из метода сечений.
Общие указания к построению эпюр изгибающих моментов и поперечных сил 1. Если поперечная сила, изменяясь непрерывно по линейному закону, проходит через нулевое значение, то в соответствующем сечении изгибающий момент имеет экстремальное (максимальное или минимальное) значение. 2. В сечении, где приложен изгибающий момент (сосредоточенная пара сил): ü на эпюре M получается скачкообразное изменение ординат – скачок, равный приложенному внешнему моменту; ü на эпюре Q никаких изменений не происходит. 3. В сечении под сосредоточенной силой: ü на эпюре M происходит резкое изменение угла наклона (излом) смежных участков эпюры; ü на эпюре Q получается скачкообразное изменение ординат – скачок, равный приложенной внешней силе. 4. В точках, соответствующих началу и концу участка, в пределах которого к балке приложена распределенная нагрузка, параболическая и прямоугольная части эпюры M сопрягаются плавно, если на границах указанного участка не приложено сосредоточенных сил. 5. В сечении на свободном или шарнирно опертом конце балки: ü изгибающий момент M равен нулю, если там не приложен внешний изгибающий момент (сосредоточенная пара сил), а если он приложен – равен этому моменту; ü поперечная сила Q равна сосредоточенной силе (внешняя сила или опорная реакция), а если сила не приложена – поперечная сила равна нулю. 6. В сечении, совпадающем с заделкой изгибающий момент M и поперечная сила Q численно равны опорным реакциям. 7. Если на некотором участке: ü ü ü
Соответствие построенных эпюрусилий изложенным выше общим указаниям также свидетельствует о правильности проведенных построений. Ломаный брус Для заданной расчетной схемы в виде ломаного бруса необходимо: 1.2.1. Провести полный кинематический анализ. 1.2.2. Построить эпюры изгибающих моментов, поперечных и продольных усилий. Пример выполнения задания. Дано: расчетная схема (рис. 1.2.1) с указанием моментов инерции ее сечений, кратных масштабу J. Требуется построить эпюры усилий в ломаном брусе.
Рис. 1.2.1 Решение Особенностью ломаного бруса в сравнении с однопролетной балкой является наличие в его сечениях продольных усилий, возникающих даже от поперечной нагрузки.
|
|


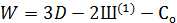
 ;
;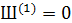 ;
; (
( 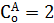 ,
,  , см. Приложение 1).
, см. Приложение 1).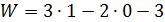 ,
,

 ;
; ;
; .
.
 ;
;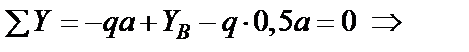
 ;
;
 .
.
 .
.




 (РВ/Н).
(РВ/Н).


 (РВ/Н).
(РВ/Н).


 (РВ/Н).
(РВ/Н).
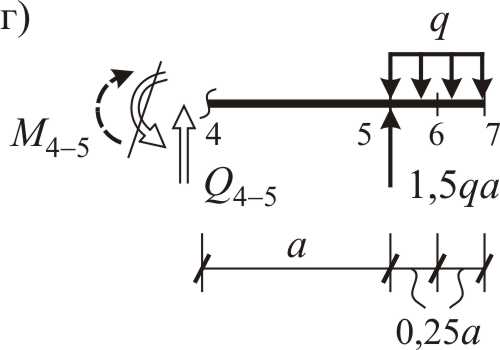 Рис. 1.1.9 (начало)
Рис. 1.1.9 (начало)

 (РВ/Н).
(РВ/Н).


 (РВ/В).
(РВ/В).


 (РВ/В).
(РВ/В).


 .
.

 .
.

 .
.

 .
.


 .
.

 и
и  ).
).


 , то изгибающий момент убывает (слева направо);
, то изгибающий момент убывает (слева направо); , то изгибающий момент возрастает (слева направо);
, то изгибающий момент возрастает (слева направо); , то изгибающий момент постоянен (чистый изгиб).
, то изгибающий момент постоянен (чистый изгиб).