|
|
Однаково розподілені випадкові величиниДля вирішення багатьох практичних завдань необхідно знати комплекс умов, завдяки якому результат сукупного впливу великої кількості випадкових чинників майже не залежить від випадку. Дані умови описані в декількох теоремах, що носять загальну назву закону великих чисел, де випадкова величина Найпростіша форма закону великих чисел - теорема Бернуллі, яка стверджує, що якщо ймовірність події однакова у всіх випробуваннях, то зі збільшенням числа випробувань частота події прагне до ймовірності події і перестає бути випадковою. Теорема Пуассона стверджує, що частота події в серії незалежних випробувань прагне до середнього арифметичного його імовірностей і перестає бути випадковою. Граничні теореми теорії ймовірностей, теореми Муавра-Лапласа пояснюють природу стійкості частоти появ події. Природа ця полягає в тому, що граничним розподілом числа появ події при необмеженому зростанні числа випробувань (якщо ймовірність події у всіх випробуваннях однакова) є нормальний розподіл. Центральна гранична теорема пояснює широке поширення нормального закону розподілу. Теорема стверджує, що завжди, коли випадкова величина утворюється в результаті складання великого числа незалежних випадкових величин з кінцевими дисперсіями, закон розподілу цієї випадкової величини виявляється практично нормальним законом. В основі якісних і кількісних тверджень закону великих чисел лежить нерівність Чебишева. Воно визначає верхню межу ймовірності того, що відхилення значення випадкової величини від її математичного сподівання більше деякого заданого числа. Чудово, що нерівність Чебишева дає оцінку ймовірності події Теорема Ляпунова. Нехай s 1, s 2, ..., s n, ... - необмежена послідовність незалежних випадкових величин з математичними очікуваннями m 1, m 2, ..., m n, ... і дисперсіями s 1 2, s 2 2, ..., s n 2 ... . Позначимо Тоді Нехай дана дискретна випадкова величина Закон великих чисел. Нехай { Інакше кажучи, ймовірність того, що середнє S n / n відрізняється від математичного очікування менше, ніж на довільно заданий Центральна гранична теорема. Нехай {
Доказ закону великих чисел Проведемо цей доказ у два етапи. Спочатку припустимо, що При t> Наступним чином: U k = якщо Якщо Тоді Нехай {f ( U 1, U 2, ..., U n. Висновок Закон великих чисел – у математичному значенні – закон теорії ймовірності, сформульованої у формі теорем Бернуллі, Пуассона і Чебишева з їхніми узагальненнями. Закон великих чисел встановлює стійкість середніх характеристик великої кількості дослідів, тобто наближених характеристик до деяких сталих величин. Названі теореми набули широкого застосування, започаткувавши один із центральних розділів теорії імовірності – граничного розподілу, а також стали одним із розділів математичної статистики. Водночас закон великих чисел у практичних дослідженнях набув закону статистики, є основою для розв'язку такої задачі за спостережуваними у реальності наслідками або подіями (явищами) знайти закони і причини цих подій. Оскільки кожна подія має свою причину, тобто породжена дією постійних і водночас випадкових причин, то закон виявляється «у формі випадковості», тобто у вигляді хаотичного коливного (розсіяного) ряду чисел. Відкриття такого закону можливе лише на основі розгляду відповідних йому подій у сукупності й обчисленні масових або середніх спостережень по них при використанні великих чисел. Однак аналіз подій у сукупності, обсяг яких завжди обмежений, дає можливість знаходити масові властивості та масові закономірності, які лише за певних умов і до того ж наближено можуть стати вираженням законів цих подій. Тобто оскільки на практиці число спроб при проведенні спостережень скінченне, то статистична величина неточно відображає закон цих подій, вона неминуче супроводжується випадковою похибкою, можливо, величина її може бути обчислена за допомогою методів теорії імовірності. Слід врахувати, що за однакового числа спостережень закономірність даних подій тим точніша, чим менша його розсіяність (дисперсія) тобто закономірність одиноких подій відображається менш точно, ніж масових (частіших) подій. Отже, за поодинокими подіями, як і за подіями з великою дисперсією, потрібно проводити велику кількість спостережень. Будь-який статистичний ряд – це коливний ряд чисел, і закон подій виражається у вигляді тенденції, що проходить між коливаннями цих чисел. Чим більше число однорідних спостережень, тим більш вираженим буде цей ряд чисел і тим точнішого виразу набуде тенденція. Збільшуючи число таких спостережень і переходячи до границі, можна отримати вираз тенденції без випадкових коливань, тобто вираз закону, що лежить в основі даної події і має назву емпіричного закону.
Список використаних джерел 1. Економічна енциклопедія: У трьох томах. Т. 1. / Редкол.: …С. В. Мочерний (відп. ред.) та ін. – К.: Видавничий центр “Академія”, 2000. – 864 с. 2. Чистяков В. П. Курс теории вероятностей, — М., 1982.
|
|
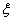 до дорівнює 1 або 0 залежно від того, чи буде результатом k-го випробування успіх або невдача. Таким чином, Sn є сумою n взаємно незалежних випадкових величин, кожна з яких приймає значення 1 і 0 з імовірностями р і q.
до дорівнює 1 або 0 залежно від того, чи буде результатом k-го випробування успіх або невдача. Таким чином, Sn є сумою n взаємно незалежних випадкових величин, кожна з яких приймає значення 1 і 0 з імовірностями р і q. для випадкової величини, розподіл якої невідомо, відомі лише її математичне сподівання і дисперсія.
для випадкової величини, розподіл якої невідомо, відомі лише її математичне сподівання і дисперсія. 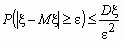 , Де M x і D x - математичне очікування і дисперсія випадкової величини x.
, Де M x і D x - математичне очікування і дисперсія випадкової величини x. 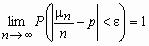 .
.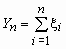 ,
, 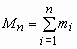 ,
, 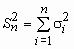 ,
, 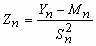 .
.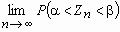 = Ф (b) - Ф (a) для будь-яких дійсних чисел a і b, де Ф (x) - функція розподілу нормального закону.
= Ф (b) - Ф (a) для будь-яких дійсних чисел a і b, де Ф (x) - функція розподілу нормального закону. = М (
= М (  > 0 при n
> 0 при n 

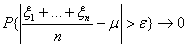 (1.2)
(1.2)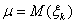 і
і  існують. Нехай Sn =
існують. Нехай Sn = 
 Ф (
Ф ( 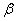 ) - Ф (
) - Ф ( 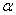 ) (1.3)
) (1.3)  більше, ніж
більше, ніж 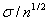 .
.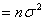 по теоремі про дисперсії суми. Згідно нерівності Чебишева, при будь-якому t> 0
по теоремі про дисперсії суми. Згідно нерівності Чебишева, при будь-якому t> 0 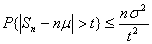 (2.1)
(2.1)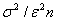 , А остання величина прагне до нуля. Це завершує першу частину докази.
, А остання величина прагне до нуля. Це завершує першу частину докази. 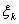 ). Цей випадок зводиться до попереднього методом зрізання.
). Цей випадок зводиться до попереднього методом зрізання. 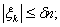 (2.2)
(2.2) 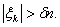
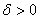 фіксовано.
фіксовано.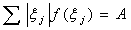 (2.4)
(2.4)  (2.5) де підсумовування проводиться по всіх тих j, при яких
(2.5) де підсумовування проводиться по всіх тих j, при яких 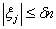 . Відзначимо, що хоча
. Відзначимо, що хоча  і залежить від п, але воно однакове для
і залежить від п, але воно однакове для