|
|
Единичная функция и переходная характеристика цепи
Единичную функцию определяют как функцию времени, равную нулю при t < 0 и равную единице при t > 0 (рис. 44,а):
а б Рис. 44
С помощью единичной функции процесс включения напряжения любой формы e(t) = f(t) на вход цепи в момент времени t = 0может быть представлен в виде произведения 1(t) f(t). Это произведение равно нулю при t < 0 и равно f(t) при t > 0. Если входной сигнал подается на цепь не в момент t = 0, а с запаздыванием на t1 (рис. 1.55, б), то его следует записать с помощью единичной функции с запаздывающим аргументом 1(t – t1) f(t). Отклик цепи на единичную функцию называется переходной характеристикой цепи и обозначается h(t) (единичную функцию можно получить на входе цепи включением в момент t = 0 или t = t1 источника с напряжением 1В). Если воздействие запаздывает на некоторое время, то на такое же время запаздывает и отклик цепи. Если воздействие увеличивается в а раз, то во столько же раз увеличивается отклик цепи. Размерность переходной характеристики цепи равна отношению размерностей выходной и входной величин. При внешнем воздействии, заданном в виде единичной функции напряжения, и отклике, являющемся тоже напряжением на каком-либо элементе цепи, переходная характеристика оказывается безразмерной величиной, численно равной выходному напряжению. Если же определяется ток в цепи, то переходная характеристика имеет размерность проводимости и называется переходной проводимостью. Для определения переходной характеристики необходимо рассчитать переходный процесс в цепи при нулевых начальных условиях при включении на вход единичной функции напряжения. Таким образом, переходная характеристика является функцией времени и определяется схемой цепи и величиной параметров элементов.
Интеграл Дюамеля
Пусть требуется найти ток в пассивном линейном двухполюснике, переходная характеристика которого известна, при включении на вход источника ЭДС сложной формы (рис. 45). Начальный запас энергии к моменту включения ЭДС считаем равным нулю.
Рис. 45
Выберем произвольно фиксированный момент наблюдения t и рассчитаем переходный ток к этому времени. Очевидно, что величину тока в этот момент определяет вся кривая входного напряжения от t = 0 до момента наблюдения t. В связи с этим введем новое обозначение текущего времени τ изменяющегося в пределах 0 ≤ τ ≤ t, и в дальнейшем будем различать e(t), i(t) как функции момента наблюдения t и e(τ) и i(τ) как функции текущего времени τ. Заменим плавную кривую e(τ) ступенчатой, что дает основание считать, в момент времени τ = 0 включается постоянное напряжение e(0)1(t), воздействующее на цепь в течение всего интервала времени от нуля до ∞. Затем через промежуток времени τ1 воздействует Δe1, затем вступает через τ2 Δe2 и т. д. Тогда
Под влиянием каждого скачка напряжения возникает переходный процесс, начинающийся в соответствующий момент τ. Под влиянием составляющей e(0)1(t) в цепи появится составляющая тока i(t) = e(0)h(t), поскольку отклик на единичную функцию есть переходная характеристика. Через τ1 под воздействием Δe11(t – τ1) в цепи появится составляющая тока Δi1 = Δe1h(t – τ1) т.к. Δe1 воздействует в промежутке времени t – τ1. В последующий момент времени τ2 вновь происходит скачкообразное изменение напряжения на величину Δe2, которое вызовет вновь составляющую тока Δi2 = Δe2h(t – τ2). Аналогично найдем, что в момент τk скачок напряжения Δek вызовет ток Δik = Δekh(t – τk). На основании метода наложения искомый переходный ток будет равен сумме составляющих, найденных для момента t, т. е.
Для того чтобы получить выражение тока, соответствующее плавно изменяющемуся входному напряжению, необходимо число скачков увеличивать до бесконечности (n → ∞), промежутки времени уменьшать до бесконечно малой величины dτ. Величину каждого скачка напряжения de можно представить в виде произведения скорости изменения напряжения de/dt на продолжительность этого промежутка dτ, т. е. Сумма в пределе перейдет в интеграл и для фиксированного момента времени значение тока будет
Полученное выражение носит название интеграла Дюамеля. Используя теорему свертки функций можно получить ещё одно выражение интеграла Дюамеля:
Пример 6. Для электрической цепи, приведенной в примере 1 рассчитать отклик на входной импульс (рис. 46).
Рис. 46 Решение. Рассчитаем переходную характеристику цепи как отклик на единичную функцию на входе. При нулевых начальных условиях изображение переходной характеристики – изображение тока в индуктивной ветви можно определить по закону Ома:
Перейдем от изображения к оригиналу по теореме разложения:
где pk – корни F2(p), в нашем случае F2(p) имеет корни p = 0, p1 = –680,
При p = 0 F1(0) = 1; При p1 = –680, При p2 = –19480, Таким образом, h(t) = 1,25∙10–2–1,3∙10–2e–680t+ 4,56∙10–4e–19480t. Соответствующий график h(t) приведен на рис. 47.
Рис. 47
Проверим правильность расчета переходной характеристики. При t = 0 h(0) должна быть равна нулю, так как переходная характеристика представляет собой ток через индуктивность при нулевых начальных условиях (на основании закона коммутации ток в индуктивности скачком измениться не может). Действительно, h(0) 0. При t → ∞ в цепи устанавливается стационарный режим, ток
Рассчитаем отклик цепи на входной сигнал.
На интервале где
Представим переходную проводимость в общем виде
где A0 = 1,25∙10–2, A1 = –1,3∙10–2, A2 = 4,56∙10–4. В течение промежутка времени от 0 до
Поскольку е(0) = 0, то первый член в выражении для искомого тока отсутствует и тогда
На интервале времени от
Следовательно,
В момент времени t = τи входное напряжение скачком уменьшается до нуля, что эквивалентно включению постоянной ЭДС обратной полярности и величиной, равной Em. Следовательно, при t > τи отклик цепи необходимо рассчитывать из выражения
График зависимости тока в индуктивной ветви от времени при заданном входном сигнале приведен на рис. 48 (для случая τи = 3/|p1|).
Рис. 48
|
|





 .
. .
.




 .
. ,
,
 .
. ;
; ;
;


 ,
, .
. ,
, ток в индуктивности
ток в индуктивности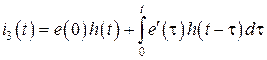 .
.


 .
. . Кроме того, при t =
. Кроме того, при t =  .
.
 .
.



 .
.

 .
.