|
|
Основная лемма вариационного исчисленияСвязь решения дифференциального уравнения 2-го порядка С нахождением минимума квадратичного функционала. Уравнение Эйлера-Лагранжа. Основная лемма вариационного Исчисления. Интегральное тождество. Естественные краевые условия
Связь решения дифференциального уравнения 2-го порядка с нахождением минимума квадратичного функционала. Пусть имеется краевая задача для дифференциального уравнения 2-го порядка:
Покажем, что математически проблема решения краевой задачи для дифференциального уравнения (на примере (1),(2)) эквивалентна задаче вариационного исчисления – о минимуме интеграла, для которого дифференциальное уравнение является уравнением Эйлера-Лагранжа. Рассмотрим функционал (интеграл)
Он получит для всякой функции Поставим задачу: найти кривую
y Пусть
(b,B)
и при достаточно малых
а b x быть
(3)
=
При малых (5¢)
Преобразуем первое слагаемое, интегрируя по частям:
которое должно быть равно нулю при любых уравнением Эйлера-Лагранжа Итак, мы установили, что функция
Уравнение, которому удовлетворяют экстремальные кривые, называется уравнением Эйлера-Лагранжа для данной вариационной проблемы. В данном случае это уравнение (6) – самосопряженное дифф. уравнение. Общее решение (6) содержит в своем составе две произвольные постоянные. Через две точки (а,А) и (в,В) можно, вообще говоря, провести одну кривую, удовлетворяющую уравнению (6). Можно показать, что именно эта кривая представляет решение экстремальной проблемы. Покажем это. Пусть
Первое слагаемое есть Замечание. Следует отметить, что всякое линейное дифф. уравнение 2-го порядка является уравнением Эйлера-Лагранжа для некоторого интеграла (функционала) типа
В общем случае для функционала
Уравнение Эйлера-Лагранжа имеет вид ( в классе гладких функций)
Действительно,
Пример. Уравнение изгиба балки
Примечания. 1) Пусть имеется функционал и граничные условия:
Соответствующее уравнение Эйлера-Лагранжа имеет вид:
(10¢)
2)
3)
Пример .
4) Методы решения дифференциальных уравнений путем минимизации функционалов (соответствующих) называют прямыми методами вариацион-ного исчисления. Методы минимизации функционалов путем решения соответствующих уравнений Эйлера-Лагранжа называются непрямымиметодами вариационного исчисления. Основная лемма вариационного исчисления
Вывод уравнений Эйлера-Лагранжа по
Если |
|

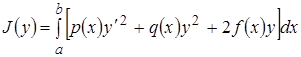 (3)
(3) , заданной при
, заданной при  , определенное значение. Таким образом, величина интеграла
, определенное значение. Таким образом, величина интеграла  зависит от выбранной кривой, т.е.
зависит от выбранной кривой, т.е.  ) и дающую минимальное значение интегралу
) и дающую минимальное значение интегралу 


 Пусть
Пусть  есть функция, дающая интегралу
есть функция, дающая интегралу  - любая непрерывная
- любая непрерывная со своей производной функция и
со своей производной функция и . Тогда
. Тогда 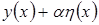



 удовлетворяет граничным условиям (2)
удовлетворяет граничным условиям (2) сколь угодно
сколь угодно (a,A)
(a,A)  близка к функции
близка к функции  дает
дает 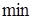
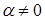 должно
должно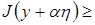
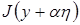 как функция от
как функция от  имеет минимум. Поэтому
имеет минимум. Поэтому (4)
(4)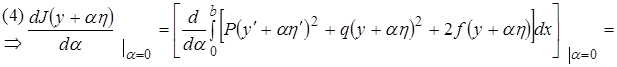
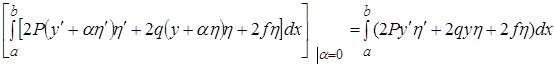 (4¢)
(4¢)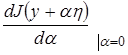 дает главную часть приращения интервала при переходе от кривой
дает главную часть приращения интервала при переходе от кривой  и это выражение называют вариацией интеграла
и это выражение называют вариацией интеграла 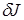 :
: , т.е. вариация
, т.е. вариация .
.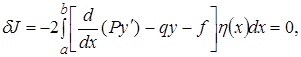 (5)
(5)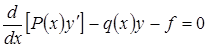 (6)
(6) необходимо должно удовлетворять уравнению (6). Значит, решение краевой задачи (1), (2) можно заменить решением вариационной задачи (3),(2).
необходимо должно удовлетворять уравнению (6). Значит, решение краевой задачи (1), (2) можно заменить решением вариационной задачи (3),(2).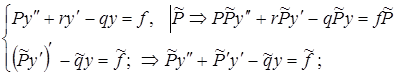

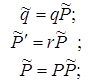

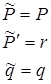
 - непрерывно дифференцируемая функция
- непрерывно дифференцируемая функция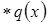 и
и  - непрерывны на
- непрерывны на  .
.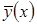 - другая функция, удовлетворяющая
- другая функция, удовлетворяющая тогда , если
тогда , если  и
и 
 (7)
(7) . Второе слагаемое с учетом условий
. Второе слагаемое с учетом условий 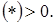 Значит
Значит 
 и
и  дает интегралу
дает интегралу  абсолютный экстремум
абсолютный экстремум  .
. умножением на
умножением на  можно
можно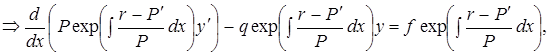 т.е.
т.е. , для которого выполняется (3).
, для которого выполняется (3). при
при  (8)
(8) ,
, 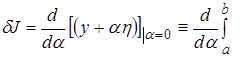
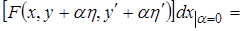
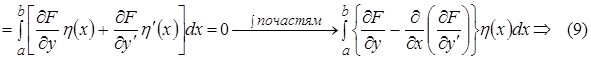
 с граничными условиями
с граничными условиями 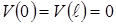 получается как уравнение Эйлера-Лагранжа из функционала:
получается как уравнение Эйлера-Лагранжа из функционала:
 .
.




 .
.  Mx q
Mx q



 z
z





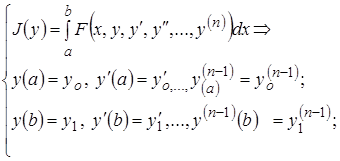
 - дифференциальное уравнение 2n порядка.
- дифференциальное уравнение 2n порядка. (11)
(11) или
или  (11¢)
(11¢)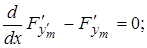
 (12)
(12) (12¢)
(12¢) дает
дает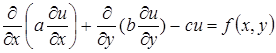
 и
и  для каждой функции
для каждой функции 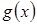 , имеющей непрерывную производную и обращающейся в нуль в точках
, имеющей непрерывную производную и обращающейся в нуль в точках  и
и  , то
, то  на
на