|
|
МЕТОДЫ СТАТИСТИЧЕСКОЙ ОЦЕНКИ ПАРАМЕТРОВ ЛИНЕЙНОЙ ЗАВИСИМОСТИФГБОУ ВПО «КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» КАФЕДРА ФИЗИКИ ЛАБОРАТОРНАЯ РАБОТА № «МОРИ» МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ Методическое указание к выполнению лабораторной работы по разделу «Механика» для студентов всех форм обучения по всем специальностям
Калининград
ОГЛАВЛЕНИЕ
Лист
1. ОБЩИЕ ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЕ УКАЗАНИЯ ........................................................................... 3 2. ВВЕДЕНИЕ ...................................... ....................................... 3 3. ОСНОВЫ ТЕОРИИ ПОГРЕШНОСТЕЙ .............................. 5 3.1. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ .... 5 3.2. ПОЛНАЯ ПОГРЕШНОСТЬ ПРЯМЫХ ИЗМЕРЕНИЙ ... 10 3.3. СЛУЧАЙНАЯ ПОГРЕШНОСТЬ…………………………… 10 3.4. ПРИБОРНАЯ ПОГРЕШНОСТЬ......................................... 11 3.5. ПОГРЕШНОСТЬ ОКРУГЛЕНИЯ .................................... 11 3.6. ПОГРЕШНОСТЬ КОСВЕННЫХ ИЗМЕРЕНИЙ………… 13 3.7. ОПРЕДЕЛЕНИЕ НЕОБХОДИМОГО КОЛИЧЕСТВА ИЗМЕРЕНИЙ .......................................................................... 14 3.8. ИСКЛЮЧЕНИЕ ПРОМАХОВ……………………………… 14 4. МЕТОДЫ СТАТИСТИЧЕСКОЙ ОЦЕНКИ ПАРАМЕТРОВ ЛИНЕЙНОЙЗАВИСИМОСТИ…………………………………. 15 4.1. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ ........................ 15 4.2. МЕТОД ПАРНЫХ ТОЧЕК ................................................. 17 4.3. ОКРУГЛЕНИЕ ОКОНЧАТЕЛЬНОГО РЕЗУЛЬТАТА ИЗМЕРЕНИЙ……………………………………………………… 18 4.4. ОСНОВНЫЕ ТРЕБОВАНИЯ К ГРАФИКУ ..................... 19 5. СПИСОК ЛИТЕРАТУРЫ ........................................................ 20 ПРИЛОЖЕНИЕ I. КОЭФФИЦИЕНТЫ СТЬЮДЕНТА ........... 21 ПРИЛОЖЕНИЕ 2. НЕОБХОДИМОЕ ЧИСЛО ИЗМЕРЕНИЙ ДЛЯ ПОЛУЧЕНИЯ ЗАДАННОЙ СЛУЧАЙНОЙ ПОГРЕШ- НОСТИ ...................................................................................... 22 ПРИЛОЖЕНИЕ 3. МАКСИМАЛЬНОЕ ОТНОСИТЕЛЬНОЕ ОТКЛОНЕНИЕ ......................................................................... 23 ПРИЛОЖЕНИЕ 4. ПРИМЕР РАСЧЁТА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ В ЛАБОРАТОРНОМ ПРАКТИКУМЕ .......... 24
ОБЩИЕ ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Методические указания предназначены для студентов I и II курсов, выполняющих лабораторные работы по курсу общей физики, и представляют собой практическое пособие для обработки результатов измерений. В них содержатся также некоторые сведения, необходимые для планирования эксперимента и анализа результатов измерений. Цель методических указаний заключается в том, чтобы научить студента самостоятельно проводить анализ результатов измерений, закрепить у него основные приемы расчёта погрешностей, научить правильно и экономно представлять графически результаты измерений. Данные методические указания могут быть также полезны студентам старших курсов в их самостоятельной научно-исследовательской работе. ВВЕДЕНИЕ Под измерением некоторой физической величины понимают процесс нахождения её значения при помощи специальных технических средств, т.е. посредством сравнения измеряемой физической величины с другой величиной, принятой за единицу измерения. При измерении любой физической величины (за исключением измерения некоторых дискретных величин) мы никогда не можем получить её истинное значение, что обусловливается как принципиально ограниченной возможностью измерительных приборов, так и природой самих измеряемых объектов. Поэтому основная задача измерений заключается не в определении истинного значения измеряемой величины, а в установлении некоторого интервала, называемого доверительным, внутри которого находится истинное значение этой величины. Другими словами, в результате измерения мы должны указать доверительный интервал (погрешность измерения) и "привязать" его к шкале значений измеряемой величины, т.е. определить положение центра доверительного интервала на шкале измеряемой величины х). Положение центра доверительного интервала на шкале значений измеряемой величины определяет её среднее арифметическое значение. В зависимости от характера измеряемой величины измерения делятся на прямые и косвенные, совокупные, совместные и т.д. Под прямыми понимают такие измерения, в которых искомая физическая величина сравнивается непосредственно с единицей измерения (эталоном), либо определяется при помощи измерительного прибора, проградуированного в соответствующих единицах. Например: а) Измерение линейных размеров тела при помощи линейки, штангенциркуля - случай непосредственного сравнения измеряемой величины с эталоном. б) Измерение температуры при помощи термометра, термометра сопротивления и т.д. Примечание. В некоторых случаях доверительный интервал не симметричен относительно среднего арифметического значения измеряемой величины. Однако в данном пособии мы ограничимся рассматриваемым выше случаем. Косвенные измерения - это такие измерения, когда измеряемая величина определяется из результатов прямых измерений других величин, которые связаны с ней некоторой функциональной связью. Например, объём цилиндра V связан с радиусом R и высотой h функциональной связью:
Измерение объёма V может быть проведено по формуле (1), то есть косвенно, если R и h известны из прямых измерений. При измерении физической величины экспериментатор получает результат измерения. Результаты измерений одной и той же величины могут различаться друг от друга в серии как из нескольких однотипных измерений, так и при использовании различных методик, приборов и т.д. Эти отклонения результатов измерения друг от друга количественно характеризуются погрешностями измерения. В зависимости от причин, вызывающих погрешности измерения, их можно разбить на три типа: систематические, промахи, случайные. I. Систематическая погрешность - это погрешность, которая либо постоянна во время измерений, либо изменяется по какому-то закону при повторных измерениях данной физической величины. Как правило, систематическая погрешность вызывается одной и той же причиной (например, тепловое расширение линейки, дрейф нуля измерительного усилителя, сбитая стрелка прибора). Различают: - систематические погрешности, природа и величина которых известна. - систематические погрешности известного происхождения, но неизвестной величины (например, люфт в микрометрической подаче, трение в опорах приборов и т.д.). Такие погрешности выявляются при
где δ – предельная абсолютная погрешность прибора; xm – предел измерения прибора. Допускаются следующие классы точности измерительных приборов 0.02; 0.05; 0.1; 0.2; 0.5; 1.0; 1.5; 2.5; 4.0. Обычно класс прибора наносится на его шкалу, либо делается отметка в паспорте прибора. - систематические погрешности, о существовании которых мы не подозреваем. Например, в процессе измерений была сбита стрелка измерительного прибора, вследствие чего все отсчёты по данному прибору будут либо завышены, либо занижены на одну и ту же величину. Такие погрешности выявляются тщательной проверкой приборов, либо сменой методики измерений. 2. Промахи - грубые ошибки, связанные, как правило, с ошибочными измерениями вследствие неправильного отсчёта по шкале измерительного прибора, неразборчивостью записей, и так далее. Измерения, содержащие промахи, должны быть отброшены как не заслуживающие доверия. Однако делать это нужно осторожно. В математической статистике существуют приёмы, позволяющие исследовать полученные результаты на предмет выявления промахов. 3. Случайная погрешность - погрешность, изменяющаяся случайным образом от измерения к измерению, вызываемая большим числом отдельных причин, действующих в каждом отдельном измерении различным образом. Благодаря тому, что случайные погрешности подчиняются определённым закономерностям, их всегда можно учесть. ОСНОВЫ ТЕОРИИ ПОГРЕШНОСТЕЙ 3.I. Элементы математической статистики Пусть в некотором эксперименте проведено N измерений некоторой величины X. Получены значения величины X, которые в общем случае отличаются друг от друга: X1; X2;. . . Xi, . . . XN (3) Если Величина
называется средним арифметическим (средним выборочным) значением измеряемой величины X. Разность
В основе теории погрешностей лежат положения, сформулированные Гауссом: - погрешности равной абсолютной величины и противоположных знаков - чем больше абсолютная погрешность, тем она менее вероятна. С учётом этих положений можно утверждать, что если Результаты измерений (3) можно представить наглядно, построив диаграмму, которая показывает частоту (вероятность) получения тех или иных значений измеряемой величины в серии (3). Такую диаграмму называют гистограммой и строят её следующим образом (рис.1). Весь диапазон изменения измеряемой величины в серии (3) разобьём на некоторое число одинаковых интервалов
Рис.1. Рис.2. Если измеряемая величина X меняется непрерывно в интервале
Вероятность получения результата измерения из некоторого конечного
Очевидно, что площадь под всей кривой p(x), как вероятность
В случае, если отклонение измеряемых величин в серии (3) обусловлены случайной погрешностью, то, как показывает опыт, плотность распределения вероятности результатов при большом числе измерений хорошо описывается функцией:
которая называется нормальной (или гауссовой) плотностью распределения вероятности. График функции (10) представлен на рис.2. Видно, что при Параметр σ в выражении (10) называется среднеквадратичным отклонением результатов измерения (среднеквадратичной погрешностью отдельного измерения) и характеризует степень разброса результатов измерения относительно среднего арифметического. Величину σ2 называют дисперсией результатов измерения. Чем больше σ, тем шире распределение (10) и тем больше вероятность заметных отклонений результатов измерения от среднего арифметического значения измеряемой величины. Следовательно, параметр σ характеризует качество измерений на данной установке, либо по данной методике. Поскольку в конкретном эксперименте число измерений N ограничено, то вместо дисперсии σ2 обычно рассматривают так называемую выборочную дисперсию S2, которая является оценкой для σ. Очевидно, что Проведем М серий измерений некоторой величины X, аналогичных серии (3), и по формуле определим средние арифметические значения измеряемой величины для каждой серии:
Очевидно, что в общем случае числа в серии (11) отличаются друг от друга и для этой последовательности можно было бы также построить гистограмму, которая при
Оказывается, что среднеквадратичные отклонения результатов в сериях (3), (11) связаны между собой:
Отсюда видно, что дисперсия средних значений измеряемой величины может быть сделана существенно меньшей, чем дисперсия результатов измерений. С учётом (13) по результатам измерений можно определить оценки среднеквадратичных отклонений результатов измерений:
Как уже указывалось ранее, в результате проведённых измерений необходимо определить интервал значений измеряемой величины (доверительный интервал), внутри которого находится её истинное значение. Предположим, что доверительный интервал известен и находится в пределах
Величина Р называется доверительной вероятностью. Чем меньше доверительный интервал, тем меньше соответствующая площадь под кривой p(X). Следовательно, вероятность того, что истинное значение величины X лежит в узком доверительном интервале, мала (P<<1) и, наоборот, с большой вероятностью (P≤1) мы можем гарантировать нахождение истинного значения в широком доверительном интервале. Но, очевидно, что в этом случае уменьшается ценность среднего арифметического, как оценки истинного значения измеряемой величины. С использованием доверительной вероятности Р окончательный результат измерения физической величины в случае, когда отклонения её обусловлены случайной погрешностью, записывается в виде :
где tP,N – коэффициент Стьюдента, определяемый по задаваемой доверительной вероятности Р и числу измерений N. Коэффициент Стьюдента учитывает отклонение реальной кривой плотности распределения результатов измерения от гауссовой кривой (10) при малом числе измерений, что, как правило, реализуется на практике. Значение доверительной вероятности Р, определяющей окончательный результат, выбирают, исходя из требований, предъявляемых к измерениям. Обычно выбирают 0,68≤Р≤0,95. Если выбрано Р=0,68, то случайная погрешность в этом случае равна среднеквадратичному отклонению
Случайная погрешность
3.2. Полная погрешность прямых измерений При проведении прямых измерений необходимо и, как правило, достаточно учитывать следующие погрешности: случайную
Порядок вычисления полной абсолютной погрешности следующий: вначале вычисляются по отдельности - случайная 3.3. Случайная погрешность. Обычно признаком присутствия в измерениях случайной погрешности является случайное отклонение измеряемой величины от измерения к измерению. В этом случае, проведя порядка десяти измерений, проводят следующие вычисления: I. По формуле (4) определяют среднее арифметическое значение измеряемой величины 2. Определяют абсолютные погрешности отдельных измерений по Если сумма этих погрешностей в серии измерений существенно отличается от нуля, необходимо увеличить число измерений. 3. Вычисляют среднеквадратичное отклонение по формуле (15) 4. Задаваясь доверительной вероятностью Р при данном числе измерений по таблице 1(см.приложение), определяют значение коэффициента Стьюдента tP,N. Тогда случайную абсолютную погрешность прямых измерений определяют по формуле: 3.4. Приборная погрешность. Приборную погрешность
где δ – предельная абсолютная погрешность прибора, вычисляется из формулы (2). λP – коэффициент, определяемый надёжностью измерения. Значения этого коэффициента: 3.5. Погрешность округления. Чтобы понять причины возникновения погрешности округления, рассмотрим пример. Предположим, что мы измеряем длину некоторого предмета штангенциркулем с ценой деления нониуса 0,01 мм. Известно, что длина предмета равна, например, 16,015 мм. Какой отсчёт мы получим по шкалам штангенциркуля? Очевидно, получим 16,01, либо 16,02. И тот и другой отсчеты правильные, так как штангенциркуль, имея цену деления нониуса 0,01 мм округляет результат измерения до 0,01 мм. Ясно, что погрешность такого округления не может превосходить половины цены деления измерителя. Аналогичные погрешности округления возникают при пользовании линейкой, микрометром, при отсчётах по шкалам стрелочных приборов, при пользовании цифровыми приборами и т.д. Абсолютная погрешность округления определяется по формуле:
где ω - интервал округления, который равен цене деления измерительного прибора, если отсчёт берется с точностью до деления, половине цены деления, если отсчёты округляются до половины цены деления и т.д. Окончательно формула для определения полной абсолютной погрешности принимает вид:
В силу разновеликости вкладов различных погрешностей в (20), как правило, нет смысла учитывать их все одновременно. В процессе измерений могут возникнуть следующие ситуации: 1. Приборная погрешность 2. Приборная погрешность существенно меньше случайной погрешности, тогда ею можно пренебречь. 3. Случайная и приборная погрешности близки друг другу. В У измерительных приборов, имеющих класс точности, погрешность округления обычно существенно меньше приборной погрешности и ею можно пренебречь. В то же время для ряда приборов (например, линейки, микрометры, штангенциркули т.д.) понятие приборной погрешности не имеет смысла и в этом случае при вычислении полной абсолютной погрешности предварительно сопоставляют погрешности случайную и округления. Полная относительная погрешность прямых измерений определяется по формуле:
где Δ – полная абсолютная погрешность,
Окончательный результат прямых измерений некоторой величины записывается в виде:
где Примечание: Вычисления случайной, приборной погрешностей и погрешности округления должны проводиться при одинаковой доверительной вероятности. Прямые измерения могут быть однократными и многократными. Выбор той или иной методики измерений определяется следующими соображениями: если измеряемая величина изменяется со временем достаточно быстро или характер её изменения неизвестен исследователю, то делают однократные измерения. Если же измеряемая величина достаточно долго остается неизменной, то делают многократные измерения. При этом могут возникнуть следующие ситуации: 1. Приборная погрешность является определяющей (то-есть существенно превосходит случайную погрешность). В этом случае достаточно провести однократное измерение. Однако, во избежание промахов, обычно делают два-три измерения. 2. Если определяющей является случайная погрешность, то делают столько измерений, чтобы средняя абсолютная погрешность (6) была невелика. Обычно достаточно сделать 5-10 измерений. 3.6.Погрешность косвенных измерений Пусть в некотором эксперименте определяются физическая величина U, являющаяся функцией нескольких аргументов X, Y, Z, t, величины которых определяются в прямых измерениях (например, в качестве U может быть плотность тела, тогда X, Y, Z, t соответственно, его линейные размеры и масса). Другими словами, задана функциональная связь:
На основании прямых измерений величин X, Y, Z, t определяют их средние значения и полные абсолютные погрешности. Подставляя средние значения аргументов в (23), получим:
либо
где ΔX, ΔY, ΔZ, Δ
3.7. Определение необходимого количества измерений Увеличивая количество измерений N даже при неизменной их точности, можно увеличить надёжность измерений либо сузить доверительный интервал. Необходимое количество измерений для достижения требуемой точности
где 3.8. Исключение промахов Существует несколько приёмов для проведения анализа и отсева грубых погрешностей измерений. Рассмотрим один из них. Если имеется некоторая выборка из генеральной совокупности с N≤25, то можно воспользоваться методом вычисления максимального относительного отклонения:
где
По таблице 3 Приложения по заданной доверительной вероятности Р находят предельное значение относительного отклонения
МЕТОДЫ СТАТИСТИЧЕСКОЙ ОЦЕНКИ ПАРАМЕТРОВ ЛИНЕЙНОЙ ЗАВИСИМОСТИ 4.I. Метод наименьших квадратов На опыте часто приходится измерять пары величин X и Y, когда одна из них является функцией другой. Проведя измерения, пытаются, как правило, найти аналитический вид такой кривой, которая проходила бы как можно ближе к экспериментальным точкам. Например, если величины X и Y связаны линейной зависимостью:
то задача исследований состоит в том, чтобы найти такие параметры m и C, при которых прямая наилучшим образом проходила бы через экспериментальные точки. Линейная зависимость существенно упрощает анализ метода наименьших квадратов. Однако, даже в случае, когда зависимость между измеряемыми величинами нелинейная, можно попытаться представить её в таких координатах, чтобы получалась линейная связь. Например, связь между сопротивлением полупроводника и температурой нелинейна:
где А, В - постоянные. Если провести замену
Предположим, что погрешность измерения величины X существенно меньше погрешности измерения Y, причём погрешностью ΔX можно пренебречь. (Такая ситуация часто реализуется в измерениях). Можно не принимать этого ограничения, но тогда анализ существенно усложняется. Отклонение результата i - го измерения от прямой можно представить так:
Сущность метода наименьших квадратов заключается в том, что оптимальное значение параметров m и C выбирается из условий минимальности суммы квадратов отклонения (32):
Рассматривая S как функцию переменных m и C, запишем условие её минимума:
Тогда искомые параметры линейной зависимости m, C могут быть найдены из системы уравнений:
Решая систему (35), найдём
Среднеквадратичные отклонения величин m и C могут быть определены по формулам:
В том случае, когда известно, что исследуемая теоретическая кривая должна проходить через начало координат (т.е. С=0), параметр m и его дисперсия могут быть найдены по формулам:
4.2. Метод парных точек В том случае, когда требуется определить лишь угол наклона прямой [по угловому коэффициенту m в (29)], нет смысла проводить громоздкие вычисления по методу наименьших квадратов. Пусть в результате измерений некоторых величин X, Y получено N точек. Возьмем пару точек 1 и (N/2)+1. Через них проходит прямая с угловым коэффициентом m1. Следующей паре точек 2 и (N/2)+2 отвечает коэффициент m2 и т.д. В результате получим N/2 значений параметра m, которые можно обработать обычным способом: найти среднее значение 4.3. Округление окончательного результата измерений Точность обработки числового материала должна быть согласована с точностью самих измерений. Вычисления, проведённые с большим числом десятичных знаков, чем это необходимо, необоснованно затрудняют вычисления. В то же время недостаточная точность вычислений ухудшает результаты измерений. Поэтому в вычислениях следует руководствоваться следующим правилом: погрешность, получающаяся в результате вычислений, должна быть по крайней мере на порядок меньше результирующей погрешности измерений. Необходимо руководствоваться следующими правилами действия над приближёнными числами: I. При сложении и вычитании в результате следует сохранить столько десятичных знаков, сколько их в приближённом числе с наименьшим числом десятичных знаков. 2. При умножении двух приближённых чисел, имеющих одинаковое число значащих цифр, окончательный результат должен содержать такое же количество значащих цифр. Если число значащих цифр в сомножителях различно, то результат должен иметь столько же значащих цифр, что и наименее точный сомножитель. 3. При возведении в степень (в том числе и в дробную) результат должен иметь столько же значащих цифр, что и основание. С другой стороны, среднеквадратичная погрешность измерений при сравнительно небольшом числе измерений (N~10) определяется с погрешностью более 30%, поэтому в результирующей погрешности следует оставлять одну значащую цифру, если она больше трёх, и две значащие цифры, если первая из них меньше четырёх. Например, если Δ = 0,635, то следует округлить Δ = 0,6, если же Δ = 0,218, то нужно оставить Δ =0,22. В среднем значении окончательного результата измерений последняя значащая цифра оставляется в том же десятичном разряде, что и последняя значащая цифра в погрешности. Ниже приведём примеры правильного и неправильного округления окончательного результата:
Неправильно: 1. (39,421±0,625) В 2. (121,37 ±2,39) с 3. (2,619·10-19±5,36·10-21) Кл 4. (19,025±0,26) г Во избежание накопления ошибок, связанных с округлением при вычислениях, рекомендуется в промежуточных расчётах сохранять число знаков на один - два больше, чем это рекомендуется вышеуказанными правилами. Примечание: Значащими цифрами числа называются все цифры от 1 до 9, а также нуль, если он стоит в середине или в конце числа. Например: число 0,39 имеет две значащих цифры, а числа 10,9 и 10,90 соответственно три и четыре значащих цифры. 4.4. Основные требования к графику 1. Наименьшее расстояние, считываемое с графика, должно быть не 2. Масштаб выбирается таковым, чтобы кривые заполняли все поле 3. Обычно на оси абсцисс откладывают аргумент, а на оси ординат –функцию. Масштаб графика должен быть простым. Лучше всего, если 1 см 4. На осях графика указывается символ, либо название измеряемой 5. Экспериментальные точки наносятся чётко без вспомогательных 6. Точки не соединяются ломаной прямой, а проводится сглаживающая кривая. 7. При сравнении теоретической кривой с данными эксперимента 8. Строят графики мягкими графитовыми карандашами. Применение 9. Если на график наносится несколько кривых, то каждой кривой
СПИСОК ЛИТЕРАТУРЫ 5.1. Зайдель А.Н. Элементарные оценки ошибок измерений. Л., Наука, 1967, 88 с. 5.2. Сквайре Дж. Практическая физика (пер. с англ.). М., Мир, 1972, 246 с. 5.3. Худсон Д. Статистика для физиков (пер. с англ.), М., Мир, 1979, 296 с. 5.4. Румшинский Л.З. Математическая обработка результатов эксперимента. М., Наука, 1971, 192 с. 5.5. ГОСТ 8.011-72 Показатели точности измерений и формы представления результатов измерения. 5.6. ГОСТ 16263-70. Метрология. Термины и определения. 5.7. Львовский Е.Н. Статистические методы построения эмпирических формул. М., Высшая школа, 1982, 224 с.
|
|
 (1)
(1) , (2)
, (2) , то говорят о полном наборе величин X или о генеральной совокупности. Реально N невелико, экспериментатор имеет дело с неполным набором величин X, который называется выборкой из генеральной совокупности.
, то говорят о полном наборе величин X или о генеральной совокупности. Реально N невелико, экспериментатор имеет дело с неполным набором величин X, который называется выборкой из генеральной совокупности. (4)
(4)
 (5)
(5) (6)
(6) и отложим их на оси абсцисс. На этих интервалах построим прямоугольники с высотой, равной
и отложим их на оси абсцисс. На этих интервалах построим прямоугольники с высотой, равной  , где
, где  - число результатов в серии (3), попавших в m-й интервал. Площади прямоугольников имеют смысл вероятности получения результата из соответствующего интервала оси абсцисс.
- число результатов в серии (3), попавших в m-й интервал. Площади прямоугольников имеют смысл вероятности получения результата из соответствующего интервала оси абсцисс.
 , а число измерений N неограниченно возрастает, то при
, а число измерений N неограниченно возрастает, то при  ,стремящемся к нулю, гистограмма, представленная на рис.1, перейдет в плавную кривую p(x), которую называют плотностью распределения вероятности результатов измерения (рис.2). Произведение
,стремящемся к нулю, гистограмма, представленная на рис.1, перейдет в плавную кривую p(x), которую называют плотностью распределения вероятности результатов измерения (рис.2). Произведение 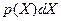 равно вероятности получения результата из интервала [X,X+dX]:
равно вероятности получения результата из интервала [X,X+dX]: (7)
(7) (8)
(8) (9)
(9) , (10)
, (10)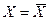 функция имеет максимум. Это означает, что чем меньше абсолютная погрешность отдельного измерения, тем она более вероятна.
функция имеет максимум. Это означает, что чем меньше абсолютная погрешность отдельного измерения, тем она более вероятна. . Поэтому далее будем рассматривать выборочную дисперсию S2 и оценку среднеквадратичного отклонения S.
. Поэтому далее будем рассматривать выборочную дисперсию S2 и оценку среднеквадратичного отклонения S.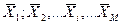 (11)
(11) перейдёт в непрерывную кривую плотности распределения вероятности средних значений измеряемой величины с параметрами
перейдёт в непрерывную кривую плотности распределения вероятности средних значений измеряемой величины с параметрами  и
и  :
: (12)
(12)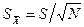 (13)
(13) (14)
(14) (15)
(15)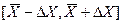 . Тогда, используя функцию плотности распределения вероятности результатов измерения (10),можно определить вероятность Р того, что истинное значение измеряемой величины находится в указанном интервале:
. Тогда, используя функцию плотности распределения вероятности результатов измерения (10),можно определить вероятность Р того, что истинное значение измеряемой величины находится в указанном интервале: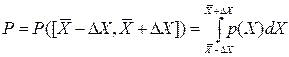 (16)
(16) , (17)
, (17) и окончательный результат записывается в виде:
и окончательный результат записывается в виде: (18)
(18) определяет абсолютное отклонение результатов измерения от истинного значения, поэтому она называется абсолютной случайной погрешностью. Отношение абсолютной случайной погрешности к среднему арифметическому значению измеряемой величины называется относительной случайной погрешностью.
определяет абсолютное отклонение результатов измерения от истинного значения, поэтому она называется абсолютной случайной погрешностью. Отношение абсолютной случайной погрешности к среднему арифметическому значению измеряемой величины называется относительной случайной погрешностью. , приборную
, приборную  и погрешность округления
и погрешность округления  . Тогда результирующая абсолютная погрешность прямых измерений может быть определена по формуле:
. Тогда результирующая абсолютная погрешность прямых измерений может быть определена по формуле: (19)
(19) , приборная
, приборная  погрешности и погрешность округления
погрешности и погрешность округления 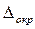 .
. .
. .
.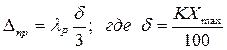 ,
, .
.
 (20)
(20) , (21)
, (21) , (22)
, (22) – нижняя и верхняя границы доверительного интервала.
– нижняя и верхняя границы доверительного интервала. (23)
(23) (24) Поскольку эта величина также является случайной, возникает вопрос об отыскании того доверительного интервала, внутри которого находится её истинное значение. Полуширина этого интервала может быть определена по формулам:
(24) Поскольку эта величина также является случайной, возникает вопрос об отыскании того доверительного интервала, внутри которого находится её истинное значение. Полуширина этого интервала может быть определена по формулам: , (25)
, (25) , (26)
, (26) – полные абсолютные погрешности прямых измерений величин X, Y, Z, t. Относительная погрешность косвенных измерений определяется по формуле:
– полные абсолютные погрешности прямых измерений величин X, Y, Z, t. Относительная погрешность косвенных измерений определяется по формуле: (27)
(27) при надёжности P можно определить, если предварительно сделать оценку среднеквадратичной погрешности измерения (по предварительным измерениям) и найти величину:
при надёжности P можно определить, если предварительно сделать оценку среднеквадратичной погрешности измерения (по предварительным измерениям) и найти величину: , (28)
, (28) ,
, – наибольшее или наименьшее (подозреваемое как промах) значение измеряемой величины;
– наибольшее или наименьшее (подозреваемое как промах) значение измеряемой величины; – среднее арифметическое значение измеряемой величина и её среднеквадратичное отклонение, вычисленные по выборке с учётом промахов по формулам (4) и (14).
– среднее арифметическое значение измеряемой величина и её среднеквадратичное отклонение, вычисленные по выборке с учётом промахов по формулам (4) и (14). . Если
. Если  ≤
≤ 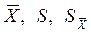 ) должны быть пересчитаны заново.
) должны быть пересчитаны заново. , (29)
, (29) , (30)
, (30) , то (30) примет вид:
, то (30) примет вид:  , то есть, получилось уравнение прямой. Поэтому, не нарушая общности, рассмотрим случай, когда величины X и Y связаны зависимостью (29). Пусть в некоторых измерениях мы получим N пар значений измеряемых величин:
, то есть, получилось уравнение прямой. Поэтому, не нарушая общности, рассмотрим случай, когда величины X и Y связаны зависимостью (29). Пусть в некоторых измерениях мы получим N пар значений измеряемых величин: (31)
(31) (32)
(32) (33)
(33) (34)
(34) (35)
(35) (36)
(36) , где (37)
, где (37) .
. (38)
(38) (39)
(39) (40)
(40) (41)
(41) и его среднеквадратичное отклонение
и его среднеквадратичное отклонение 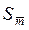 . Окончательный результат запишется в виде
. Окончательный результат запишется в виде 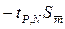 до
до  . Следует отметить, что при нахождении параметра m нет необходимости строить экспериментальный график.
. Следует отметить, что при нахождении параметра m нет необходимости строить экспериментальный график.