|
|
Метод узловых потенциалов в матричной формеМетод контурных токов в матричной форме В соответствии с введенным ранее понятием матрицы главныхконтуровВ, записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам. Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c=n-m+1. Выражение (6) запишем следующим образом:
В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j–го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j–й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения
где С учетом (8) соотношение (7) можно записать, как:
Полученное уравнение представляет собойконтурные уравнения вматричной форме. Если обозначить
то получим матричную форму записи уравнений, составленных по методу контурных токов:
где В развернутой форме (12) можно записать, как:
Рассмотрим пример составления контурных уравнений. Пусть имеем схему по рис. 2. Данная схема имеет четыре узла (m=4) и шесть обобщенных ветвей (n=6). Число независимых контуров, равное числу ветвей связи, c=n-m+1=6-4+1=3. Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.
.Диагональная матрица сопротивлений ветвей
Матрица контурных сопротивлений
Матрицы ЭДС и токов источников
Тогда матрица контурных ЭДС
Матрица контурных токов
Таким образом, окончательно получаем: где Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
где МатрицыZ и Y взаимно обратны. Умножив обе части равенства (14) на узловую матрицуАи учитывая первый закон Кирхгофа, согласно которому
получим:
Выражение (16) перепишем, как:
Принимая потенциал узла, для которого отсутствует строка в матрице А, равным нулю, определим напряжения на зажимах ветвей:
Тогда получаем матричное уравнение вида:
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
где В развернутом виде соотношение (22) можно записать, как:
то есть получили известный из метода узловых потенциалов результат. Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
Данная схема имеет 3 узла (m=3) и 5 ветвей (n=5). Граф схемы с выбранной ориентацией ветвей представлен на рис. 5. Узловая матрица (примем
Диагональная матрица проводимостей ветвей:
где Матрица узловых проводимостей
Матрицы токов и ЭДС источников
. .Следовательно, матрица узловых токов будет иметь вид:
.Таким образом, окончательно получаем: где Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов. Литература
Контрольные вопросы и задачи
Ответ: .
Ответ:
|
| Теория / ТОЭ / Лекция N 7. Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. |
Передача энергии w по электрической цепи (например, по линии электропередачи), рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, то есть тем, сколько энергии передается по линии в единицу времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи или преобразования энергии называется мощностью р. Сказанному соответствует математическое определение:
Выражение для мгновенного значения мощности в электрических цепях имеет вид:
Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за
Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока. Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания. Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику в течение времени t равна Среднее за период значение мгновенной мощности называется активной мощностью Принимая во внимание, что
Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию), поэтому |
|
 .
.
 ,
,
 - столбцовая матрица контурных токов;
- столбцовая матрица контурных токов;  - транспонированная контурная матрица.
- транспонированная контурная матрица.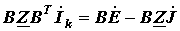
 ,
,
 .
.
 ,
,
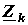 - матрица контурных сопротивлений;
- матрица контурных сопротивлений;  - матрица контурных ЭДС.
- матрица контурных ЭДС. ,
,
 то есть получили известный из метода контурных токов результат.
то есть получили известный из метода контурных токов результат. Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:
Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:



 .
.





 .
.
 .
.
 ,
, ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
. ,
,

 - диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю.
- диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю. ,
,
 . .
. .
 .
.
 .
.
 .
.

 ,
,

 - матрица узловых проводимостей;
- матрица узловых проводимостей;  - матрица узловых токов.
- матрица узловых токов.


 )
)
 ,
,
 .
.
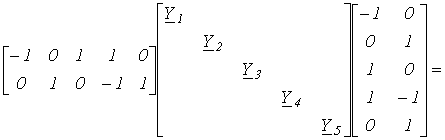
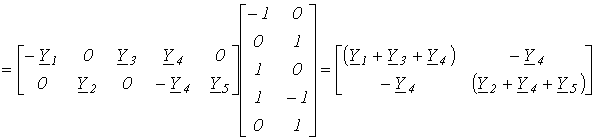 .
.



 ,
, ;
;  ;
;  ;
;  ;
; 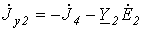 .
. .
.
 .
.
 , получим:
, получим: .
.

 .
. .
. , из (3) получим:
, из (3) получим: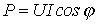 .
.
 , т.е. на входе пассивного двухполюсника
, т.е. на входе пассивного двухполюсника  . Случай Р=0,
. Случай Р=0, 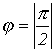 теоретически возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего только идеальные индуктивные и емкостные элементы.
теоретически возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего только идеальные индуктивные и емкостные элементы.