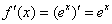|
|
Понятие суммы степенного рядаНачнем подходить к теме с воспоминаний. Как мы помним, любой числовой ряд может или сходиться, или расходиться. Если числовой ряд На уроке Степенные ряды. Область сходимости ряда мы рассматривали уже не числовые, а функциональные и степенные ряды. Возьмём тот самый подопытный степенной ряд, который всем понравился:
Еще раз подчеркиваю, что данный факт справедлив только для найденной области Чтобы всё стало окончательно понятно, рассмотрим примеры с картинками. Я выпишу простейшее табличное разложение синуса в степенной ряд:
(По какому принципу получены сами элементарные табличные разложения, мы рассмотрим чуть позже). Теперь вспоминаем школьный график синуса Вот такая симпатичная синусоида. Хмм…. Где-то я уже это видел…. Теперь фишка. Если начертить график бесконечного многочлена А что значит вообще «сходится»? По смыслу глагола – что-то куда-то идёт. Если я возьму первые три члена ряда Рассмотрим более печальный пример, табличное разложение арктангенса: Печаль заключается в том факте, что график бесконечного многочлена
Вне отрезка
Разложение функций в степенной ряд. Приступим к увлекательному занятию – разложению различных функций в степенные ряды. Сначала пара формул, затем практические задания. Если функция Данная формула получила имя некоего англичанина Тейлора (ударение на первый слог). На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда Это разложение в ряд обычно называют именем шотландца Маклорена (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора по степеням Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции: Теперь начинаем находить производные в точке ноль: первую производную, вторую производную, третью производную и т.д. Это просто, поскольку при дифференцировании экспонента превращается в саму себя:
Совершенно очевидно, что Подставляем единицы в формулу Маклорена и получаем наше табличное разложение! Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).
|
|
 сходится, то это значит, что сумма его членов равна некоторому конечному числу:
сходится, то это значит, что сумма его членов равна некоторому конечному числу: 
 . В ходе исследования было установлено, что этот ряд сходится при
. В ходе исследования было установлено, что этот ряд сходится при  . Если числовые ряды сходятся к ЧИСЛАМ, то к чему же сходятся функциональные и степенные ряды? Правильно подумали. Функциональные ряды сходятся к ФУНКЦИЯМ. В частности, суммой ряда
. Если числовые ряды сходятся к ЧИСЛАМ, то к чему же сходятся функциональные и степенные ряды? Правильно подумали. Функциональные ряды сходятся к ФУНКЦИЯМ. В частности, суммой ряда  :
:


 :
:
 , то получится… та же самая синусоида! То есть, наш степенной ряд
, то получится… та же самая синусоида! То есть, наш степенной ряд  сходится к функции
сходится к функции  и начерчу график многочлена пятой степени, то он лишь отдаленно будет напоминать синусоиду. А вот если составить многочлен из первых ста членов ряда:
и начерчу график многочлена пятой степени, то он лишь отдаленно будет напоминать синусоиду. А вот если составить многочлен из первых ста членов ряда:  и начертить его график, то он будет с синусоидой практически совпадать. Чем больше членов ряда – тем лучше приближение. И, как уже отмечалось, график бесконечного многочлена – есть в точности синусоида. Иными словами, ряд
и начертить его график, то он будет с синусоидой практически совпадать. Чем больше членов ряда – тем лучше приближение. И, как уже отмечалось, график бесконечного многочлена – есть в точности синусоида. Иными словами, ряд 

 совпадает с графиком арктангенса
совпадает с графиком арктангенса  только на отрезке
только на отрезке  (т.е. в области сходимости ряда):
(т.е. в области сходимости ряда):
 расходится, а график бесконечного многочлена пускается во все тяжкие и уходит на бесконечность.
расходится, а график бесконечного многочлена пускается во все тяжкие и уходит на бесконечность. , то это разложение единственно и задается формулой:
, то это разложение единственно и задается формулой:
 в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву
в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву  .
. :
:
 .
.

 , тогда:
, тогда: