|
|
Результаты практической работыСанкт-Петербург Издательство Политехнического университета УДК 528.48(075.8)
Инженерная геодезия. Решение инженерных задач на планах и картах: Учеб. пособие / Н.Д. Беляев, Ф.Н. Духовской, Н.Н. Загрядская, Е.Б. Михаленко. СПб.: Изд-во Политехн. ун-та, 2004. 66 с.
Пособие соответствует государственному стандарту по направлению 550100 «Строительство». Приведены основные сведения о современных топографических картах. Даны характеристики карт и планов, рассмотрены способы изображения рельефа, контуров и объектов местности, различные системы координат, применяемые в геодезии, номенклатура топографических карт и планов. Подробно изложена методика измерений по картам. Рассматриваются определение высот (отметок) и плановых координат точек, построение профилей, измерение площадей. Даются способы математической обработки результатов геодезических измерений и оценки их точности. Предназначено для студентов инженерно-строительного факультета в пределах программы бакалавриата.
Табл. 2. Ил. 51. Библиогр.: 5 назв.
Печатается по решению редакционно-издательского совета Санкт-Петербургского государственного политехнического университета.
ã Санкт-Петербургский государственный политехнический университет, 2004
ВВЕДЕНИЕ
Структуру и содержание учебного пособия определили программа, общий лимит времени, который отводится на дисциплину «Инженерная геодезия» на инженерно-строительном факультете (порядка 100 часов), принятая лекционно-практическая форма обучения. Лекционно-практический метод предусматривает такую форму обучения, когда положения теории во всех необходимых случаях сразу же закрепляются практическими упражнениями – решением задач, выполнением работ. При этом, в зависимости от содержания темы, решение отдельных задач выполняется преподавателем. Соответственно в тексте приведены рекомендуемые задачи. В других случаях после законченного изложения теории вопроса практическая часть приводится в конце параграфа. Здесь предусматривается самостоятельная работа студентов, но с помощью и под контролем преподавателя. Комплексное освоение материала курса осуществляется при самостоятельном выполнении студентами расчетно-графических работ.
ФОРМА И РАЗМЕРЫ ЗЕМЛИ
Общая форма Земли, как материального тела, определяется действием внутренних и внешних сил на ее частицы. Если бы Земля была неподвижным однородным телом и подвергалась действию только внутренних сил тяготения, она имела бы форму шара. Действие центробежной силы, вызванной вращением Земли вокруг ее оси, определяет сплюснутость Земли у полюсов. Под воздействием внутренних и внешних сил физическая (топографическая) поверхность Земли образует фигуру неправильной, сложной формы. Одновременно на физической поверхности Земли встречаются самые различные неровности: горы, хребты, долины, котловины и т. д. Описать такую фигуру при помощи каких-либо аналитических зависимостей невозможно. В то же время для решения геодезических задач в конечном виде необходимо основываться на определенной математически строгой фигуре – только тогда возможно получение расчетных формул. Исходя из этого задачу по определению формы и размеров Земли принято делить на две части: 1) установление формы и размеров некоторой типичной фигуры, представляющей Землю в общем виде; 2) изучение отступлений физической поверхности Земли от этой типичной фигуры. Известно, что 71 % земной поверхности покрывают моря и океаны, суши – только 29 %. Поверхность же морей и океанов характерна тем, что она в любой точке перпендикулярна к отвесной линии, т.е. направлению действия силы тяжести (если вода находится в спокойном состоянии). Направление действия силы тяжести можно установить в любой точке и соответственно построить поверхность, перпендикулярную к направлению этой силы. Замкнутая поверхность, которая в любой точке перпендикулярна к направлению действия силы тяжести, т.е. перпендикулярна к отвесной линии, называется уровенной поверхностью. Уровенная поверхность, совпадающая со средним уровнем воды в морях и океанах в их спокойном состоянии и мысленно продолженная под материками, называется основной (исходной, нулевой) уровенной поверхностью. В геодезии за общую фигуру Земли принимают фигуру, ограниченную основной уровенной поверхностью, и такую фигуру именуют геоидом (рис. 1).
Вследствие особой сложности, геометрической неправильности геоида, его заменяют другой фигурой – эллипсоидом, образующимся при вращении эллипса вокруг его малой оси РР1(рис. 2). Размеры эллипсоида определялись неоднократно учеными ряда стран. В Российской Федерации они были вычислены под руководством профессора Ф.Н. Красовского в 1940 г. и в 1946 г. постановлением Совета Министров СССР были утверждены: большая полуось а = 6 378 245 м, малая полуось b = 6 356 863 м, сжатие
Земной эллипсоид ориентируют в теле Земли так, чтобы его поверхность в наибольшей мере соответствовала поверхности геоида. Эллипсоид с определенными размерами и определенным образом ориентированный в теле Земли называется референц-эллипсоидом (сфероидом). Наибольшие отклонения геоида от сфероида составляют 100–150 м. В тех случаях, когда при решении практических задач фигуру Земли принимают за шар, радиус шара, равновеликого по объему эллипсоиду Красовского, составляет R = 6 371 110 м = 6371,11 км.
Рис. 3 При решении практических задач в качестве типичной фигуры Земли принимают сфероид или шар, а для небольших участков кривизну Земли вообще не учитывают. Такие отступления целесообразны, так как упрощается проведение геодезических работ. Но эти отступления приводят к искажениям при отображении физической поверхности Земли тем методом, который принято именовать в геодезии методом проекций. Метод проекций при составлении карт и планов заключается в том, что точки физической поверхности Земли А, В и так далее проектируются отвесными линиями на уровенную поверхность (см. рис. 3,а,б). Точки а, b и так далее называются горизонтальными проекциями соответствующих точек физической поверхности. Затем определяется положение этих точек на уровенной поверхности с помощью различных систем координат, и тогда их можно нанести на лист бумаги, т. е. на лист бумаги будет нанесен отрезок ab, который является горизонтальной проекцией отрезка AВ. Но, чтобы по горизонтальной проекции определить действительное значение отрезка AВ, необходимо знать длины аА и bВ (см. рис. 3,б), т.е. расстояния от точек A и В до уровенной поверхности. Эти расстояния называются абсолютными высотами точек местности. Таким образом, задача составления карт и планов распадается на две: определение положения горизонтальных проекций точек; определение высот точек местности. При проектировании точек на плоскость, а не на уровенную поверхность, появляются искажения: вместо отрезка ab будет отрезок а'b' вместо высот точек местности аА и bВ будут а'А и b'В (см. рис. 3,а,б). Итак, длины горизонтальных проекций отрезков и высоты точек будут различны и при проектировании на уровенную поверхность, т.е. при учете кривизны Земли, и при проектировании на плоскость, когда кривизна Земли не учитывается (рис. 4). Эти различия будут наблюдаться в длинах проекций DS = t – S, в высотах точек Dh = b'О – bО = b'О – R. Задача в отношении учета кривизны Земли сводится к следующему: принимая Землю за шар с радиусом R,необходимо определить, для какого наибольшего значения отрезка S можно не учитывать кривизну Земли при условии, что в настоящее время относительная погрешность
Рис. 4
Следовательно, участок сферической поверхности Земли диаметром в 20 км можно принимать за плоскость, т.е. кривизну Земли в пределах такого участка, исходя из погрешности Искажение в высоте точки Dh = b'О – bО = Rseca – R = R(seca – 1). Принимая
В инженерно-геодезических работах допускаемая погрешность обычно составляет не более 5 см на 1 км, и поэтому кривизну Земли следует учитывать при сравнительно небольших расстояниях между точками, порядка 0,8 м. ОБЩИЕ ПОНЯТИЯ О КАРТАХ, ПЛАНАХ И ПРОФИЛЯХ
Главное отличие плана от карты заключается в том, что при изображении участков земной поверхности на плане горизонтальные проекции соответствующих отрезков наносят без учета кривизны Земли. При составлении карт кривизну Земли приходится учитывать. Практические потребности в точности изображения участков земной поверхности различны. При составлении проектов строительных объектов они значительно выше, чем при общем изучении территории района, геологических обследованиях и т.д. Известно, что с учетомдопустимой погрешности при измерении расстояний DS = 1 см на 10 км участок сферической поверхности Земли диаметром в 20 км можно принимать за плоскость, т.е. кривизну Земли для такого участка можно не учитывать. Соответственно создание плана схематически можно представить следующим образом. Непосредственно на местности (см. рис. 3,а) измеряют расстояния АВ, ВС … , горизонтальные углы b1; b2 … и углы наклона линий к горизонту n1, n2 ... . Затем от измеренной длины линии местности, например AB, переходят к длине ее ортогональной проекции а'b' на горизонтальной плоскости, т.е. определяют горизонтальное проложение этой линии по формуле а'b' = ABcosn, и, уменьшая в определенное число раз (масштаб), откладывают отрезок а'b' на бумаге. Вычислив аналогичным путем горизонтальные проложения других линий, получают на бумаге многоугольник (уменьшенный и подобный многоугольнику а'b'c'd'е'), который является планом контура местности АВСDЕ. План – уменьшенное и подобное изображение на плоскости горизонтальной проекции небольшого участка земной поверхности без учета кривизны Земли. Планы принято подразделять по содержанию и масштабу. Если на плане изображены только местные объекты, то такой план называют контурным (ситуационным). Если дополнительно на плане отображен рельеф, то такой план называют топографическим. Стандартные масштабы планов 1:500; 1:1000; 1:2000; 1:5000. Карты обычно разрабатывают для обширной части земной поверхности, при этом приходится учитывать кривизну Земли. Изображение участка эллипсоида или шара нельзя перенести на бумагу без разрывов. В то же время соответствующие карты предназначаются для решения конкретных задач, например для определения расстояний, площадей участков и т.д. При разработке карт задача состоит не в полном устранении искажений, что невозможно, а в уменьшении искажений и математическом определении их значений с тем, чтобы по искаженным изображениям можно было вычислить действительные величины. Для этого применяют картографические проекции, дающие возможность изображать на плоскости поверхность сфероида или шара по математическим законам, обеспечивающим измерения по карте. Различные требования к картам определили наличие многих картографических проекций, которые подразделяют на равноугольные, равновеликие и произвольные. В равноугольных (конформных) проекциях сфероида на плоскость сохраняются углы изображаемых фигур, но масштаб при переходе от точки к точке изменяется, что приводит к искажению фигур конечных размеров. Однако небольшие участки карты, в пределах которых изменения масштаба не имеют существенного значения, можно рассматривать и использовать как план. В проекциях равновеликих (эквивалентных) сохраняется отношение площадей любых фигур на сфероиде и на карте, т.е. масштабы площадей везде одинаковы (при отличающихся масштабах по различным направлениям). В произвольных проекциях не соблюдается ни равноугольность, ни равновеликость. Они применяются для мелкомасштабных обзорных карт, а также для специальных карт в тех случаях, когда карты обладают каким-либо специфическим полезным свойством. Карта – построенное по определенным математическим законам, уменьшенное и обобщенное изображение поверхности Земли на плоскости. Карты принято подразделять по содержанию, назначению и масштабу. По содержанию карты бывают общегеографические и тематические, по назначению – универсальные и специальные. Общегеографические карты универсального назначения отображают земную поверхность с показом всех ее основных элементов (населенные пункты, гидрография и т.д.). Математическая основа, содержание и оформление специальных карт подчиняются их целевому назначению (карты морские, авиационные и многие другие сравнительно узкого назначения). По масштабам карты условно делят на три вида: крупномасштабные (1:10 000 и крупнее); среднемасштабные (1:200 000 – 1:1 000 000); мелкомасштабные (мельче 1:1 000 000). Карты, подобно планам, бывают контурными и топографическими. В Российской Федерации государственные топографические карты издают в масштабах 1:1 000 000 – 1:10 000. В тех случаях, когда карты или планы используют для проектирования инженерных сооружений, для получения оптимального решения особое значение приобретает наглядность в отношении физической поверхности Земли по какому-либо направлению. Например, при проектировании линейных сооружений (дорог, каналов и т.д.) необходимы: детальная оценка крутизны скатов на отдельных участках трассы, ясное представление о почвенно-грунтовых и гидрологических условиях местности, по которой проходит трасса. Такую наглядность, позволяющую принимать обоснованные инженерные решения, обеспечивают профили. Профиль – изображение на плоскости вертикального разреза земной поверхности по заданному направлению. Чтобы неровности земной поверхности были более заметными, вертикальный масштаб следует выбирать крупнее горизонтального (обычно в 10–20 раз). Таким образом, как правило, профиль является не подобным, а искаженным изображением вертикального разреза земной поверхности.
МАСШТАБЫ
Горизонтальные проекции отрезков (см. рис. 3,б отрезки ab или а'b')при составлении карт и планов изображают на бумаге в уменьшенном виде. Степень такого уменьшения характеризуется масштабом. Масштаб карты (плана) – отношение длины линии на карте (плане) к длине горизонтального проложения соответствующей линии местности:
Масштабы бывают численные и графические. Численный масштаб фиксируют двумя способами. 1. В виде простой дроби 2. В виде именованного соотношения, например в 1 см 20 м. Целесообразность такого соотношения определяется тем, что при изучении местности по карте удобно и привычно оценивать длину отрезков на карте в сантиметрах, а длину горизонтальных проложений на местности представлять в метрах или километрах. Для этого численный масштаб преобразовывают в разнотипные единицы измерения: 1 см карты соответствует такому-то количеству метров (километров) местности. Пример 1.На плане Решение: 1,5 ´ 5000 = 7500 см = 75 м (или 1,5 ´ 50 = 75 м). Пример 2. Горизонтальное проложение между двумя точками на местности равно 40 м. Чему будет равно расстояние между этими же точками на плане М = 1:2000 (в 1 см 20 м)? Решение: Чтобы избежать вычислений и ускорить работу, пользуются графическими масштабами. Таких масштабов два: линейный и поперечный. Для построения линейного масштаба выбирают исходный отрезок, удобный для данного масштаба (чаще длиной 2 см). Этот исходный отрезок называется основанием масштаба (рис. 5). Основание откладывают на прямой линии необходимое число раз, крайнее левое основание делят на части (обычно на 10 частей). Затем линейный масштаб подписывают, исходя из того численного масштаба, для которого он строится (на рис. 5,а для М = 1:25 000). Такой линейный масштаб позволяет определенным образом оценить отрезок с точностью в 0,1 доли основания, дополнительную часть этой доли приходится оценивать на глаз. Для обеспечения необходимой точности измерений угол между плоскостью карты и каждой ножкой циркуля-измерителя (рис. 5,б)не должен быть менее 60°, и измерение длины отрезка следует произвести не менее двух раз. Расхождение DS(в метрах) между результатами измерений должно быть
Рис. 5
Если отрезок длиннее построенного линейного масштаба, то его измеряют по частям. В этом случае расхождение между результатами измерения в прямом и обратном направлениях не должно превышать Для более точных измерений пользуются поперечным масштабом, имеющим на линейном масштабе дополнительное построение по вертикали (рис. 6).
Рис. 6
После того как необходимое количество оснований масштаба отложено (также обычно длиной 2 см, тогда масштаб называется нормальным), восстанавливают перпендикуляры к исходной линии и делят их на равные отрезки (на m частей). Если основание разделено на п частей и точки деления верхнего и нижнего основания соединены наклоннымилиниями (трансверсалями) так, как показано на рис. 6, то отрезок Поперечный масштаб гравируют на металлических линейках, которые называются масштабными. Перед применением масштабной линейки следует оценить основание и его доли по следующей схеме. Пусть численный масштаб 1:5000, именованное соотношение будет: в 1 см 50 м. Если поперечный масштаб нормальный (основание 2см, рис. 7), то основание составит 100 м; 0,1 основания – 10 м; 0,01 основания – 1 м. Задача по отложению отрезка заданной длины сводится к определению числа оснований, его десятых и сотых долей и, в необходимых случаях, к глазомерному определению части его наименьшей доли. Пусть, например, требуется отложить отрезок d = 173,35 м, т.е. требуется взять в раствор измерителя: 1 основание +7 (0,1 основания) +3 (0,01 основания) и на глаз расположить ножки измерителя между горизонтальными линиями 3 и 4 (см. рис. 7) так, чтобы линия АБ отсекала 0,35 промежутка между этими линиями (отрезок ДЕ). Обратная задача (определение длины отрезка, взятого в раствор измерителя) соответственно и решается в обратном порядке. Добившись совмещения игл измерителя с соответствующими вертикальной и наклонной линиями так, чтобы обе ножки измерителя находились на одной горизонтальной линии, считываем количество оснований и его долей (dBГ = 235,3 м).
Рис. 7
При проведении съемок местности для получения планов неизбежно возникает вопрос: какие наименьшие размеры объектов местности должны отобразиться на плане? Очевидно, чем крупнее масштаб съемки, тем меньше будет линейный размер таких объектов. Для того чтобы применительно к конкретному масштабу плана можно было принять определенное решение, вводится понятие о точности масштаба. При этом исходят из следующего. Опытным путем установлено, что измерить расстояние, пользуясь циркулем и масштабной линейкой, точнее, чем 0,1 мм, невозможно. Соответственно под точностью масштаба понимают длину отрезка на местности, соответствующую 0,1 мм на плане данного масштаба. Так, если М 1:2000, то точность будет: Следует иметь в виду, что при измерениях на плане взаимного положения контуров точность определяется не графической точностью, а точностью самого плана, где ошибки могут составлять в среднем 0,5 мм вследствие влияния других, кроме графических, погрешностей.
Практическая часть
I. Решите следующие задачи. 1. Определите численный масштаб, если горизонтальное проложение линии местности длиною 50 м на плане выражается отрезком в 5 см. 2. На плане II. Постройте линейный масштаб, для чего проведите линию длиной 8 см (см. рис. 5,а). Выбрав основание масштаба длиной 2 см, отложите 4 основания, крайнее левое основание разделите на 10 частей, произведите оцифровку для трех масштабов: III. Решите следующие задачи. 1. Отложите на бумаге в трех указанных масштабах отрезок длиной 144 м. 2. Пользуясь линейным масштабом учебной карты IV. Пользуясь масштабной линейкой, решите следующие задачи. 1. Отложите на бумаге длину линий местности, оформив результаты упражнения в табл. 1. Таблица 1 Результаты практической работы
УСЛОВНЫЕ ЗНАКИ
Объекты местности изображают на планах и картах условными знаками. Но одни объекты имеют значительные размеры (например, озеро, лес и т.д.), другие объекты малы (колодец, мост и т.д.). Объекты, размеры которых значительны, отображают в масштабе данной карты с сохранением подобия контуров, для малых объектов такое отображение невозможно. Кроме того, и большие и малые объекты необходимо сопроводить определенными характеристиками (для древостоя указать его среднюю высоту, для моста – грузоподъемность и т.д.). В связи с этим все условные знаки делят на три группы: масштабные (контурные), внемасштабные и пояснительные. Масштабные (рис. 8) служат для изображения объектов в масштабе карты или плана. Контур такого объекта наносится точечным пунктиром или тонкой сплошной линией и заполняется значками, отличающими его от других объектов. Внемасштабные условные знаки (рис. 9) применяют для изображения объектов, не выражающихся в данном масштабе. По ним невозможно судить о размерах объекта, но определенная точка знака соответствует положению объекта на местности. Такие знаки используют и для изображения объектов линейного характера (дороги, линии связи и т.д.). Они позволяют передать точное местоположение объектов по их оси.
Промежуточное положение между масштабными и внемасштабными занимают линейные условные знаки, являющиеся по длине масштабными, а по ширине внемасштабными. Пояснительные условные знаки (рис. 10), представленные значком, числом, надписью или их совокупностью, служат для дополнительной характеристики объектов.
Рис. 10
Условные знаки применительно к различным масштабам приводятся в специальных каталогах, издаваемых Главным управлением геодезии и картографии (ГУГК), и являются обязательными для всех учреждений. Точное воспроизведение условных знаков – одно из основных требований при вычерчивании плана.
Практическая часть
По двум каталогам условных знаков (для крупного и мелкого масштабов) сопоставить изображения нижеследующих объектов в масштабах 1. Точки плановых съемочных сетей. 2. Постройки огнестойкие жилые. 3. Линии электропередачи. 4. Воздушные проводные линии связи. 5. Шоссе. 6. Откосы спланированные неукрепленные. 7. Обрывы. 8. Леса. 9. Отдельно стоящие деревья. 10. Сплошные заросли кустарников. 11. Луговая травянистая растительность. 12. Пашни, огороды. Утвержденные требования к воспроизведению условных знаков приводятся в конце каталогов, в разделе «Пояснения к условным знакам».
ИЗМЕРЕНИЕ ОТРЕЗКОВ
Отрезки, длину которых необходимо определить, могут быть прямыми, ломаными и криволинейными. Измерение прямолинейных отрезков между точками производят с графической погрешностью 0,1 мм, расхождение между повторными измерениями данного отрезка не должно превосходить 0,3 мм.
Рис. 11
Измерение ломаных отрезков производят по частям или путем их последовательного спрямления (способ наращивания). При этом способе (рис. 11) устанавливают ножки измерителя в точках а и б, совмещают край линейки с направлением б–в, вращают измеритель вокруг ножки в точке б и устанавливают вторую ножку измерителя у края линейки в точке а1,т.е. на продолжении отрезка бв. После этого перемещают ножку циркуля из точки б в точку в и получают сумму отрезков аб и бв. Действуя аналогично, получают в растворе циркуля а3д общую длину ломаной линии абвгд. Для контроля измерения проводят в обратном направлении, от точки д к точке а. Для измерения криволинейных отрезков применяются специальные приборы – курвиметр, циркуль-измеритель с постоянным раствором, а также существует способ наращивания. Курвиметр состоит из колесика, связанного со стрелкой, которая указывает на циферблате длину линии в сантиметрах. Удерживая курвиметр перпендикулярно к плоскости карты, ведут его колесико по измеряемому отрезку. Перед применением курвиметра необходимо определить цену его деления. Для этого выбирают отрезок известной длины и устанавливают, какое число делений курвиметра п будет соответствовать этому отрезку. Тогда цена деления курвиметра
Перед началом измерения отсчет на циферблате курвиметра выводят на 0. Применение циркуля-измерителя с постоянным раствором сводится к измерению малых хорд. Берут раствор циркуля порядка двух-пяти миллиметров и определяют по отрезку с известной длиной dизв длину отрезка, взятого в раствор циркуля:
где п – число перестановок циркуля. После определения dраст измеряют длину криволинейного отрезка. Для измерений следует пользоваться циркулем с регулирующим винтом, dраст следует брать меньше при большей извилистости измеряемой линии. Применение способа наращивания при измерении криволинейных отрезков такое же, как и при измерении ломаных отрезков (измеряют малые хорды, на которые делится криволинейный отрезок). Практика измерений криволинейных отрезков показывает, что наиболее точным является применение циркуля-измерителя с постоянным раствором.
Практическая часть
Сопоставьте точность измерения прямолинейного отрезка тремя способами: по масштабной линейке, циркулем-измерителем с постоянным раствором, с помощью курвиметра. Перед измерениями, пользуясь графиком линейного масштаба учебной карты, определите цену деления курвиметра ски длину отрезка, взятого в раствор циркуля dраст. Измерьте на карте ломаную линию (длину контура: участка, относящегося к населенному пункту) двумя способами: по частям с помощью масштабной линейки и способом наращивания. Измерьте с помощью курвиметра два криволинейных отрезка: участок реки между сторонами километровой сетки (длина 12–14 см) и участок проселочной дороги.
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ
Границы участков, площади которых необходимо определить на плане или карте, могут иметь прямолинейное или произвольное очертание. При прямолинейных очертаниях определение площади возможно двумя способами: графическим (по расчетным формулам конкретных геометрических фигур) и аналитическим (по координатам вершин углов многоугольника).
Рис. 12
В первом случае участок разбивают преимущественно на треугольники, реже на прямоугольники и трапеции (рис. 12). Измеряют линейные элементы (стороны, высоты) и по формулам геометрии вычисляют площади каждой фигуры. Для контроля площади вычисляют дважды, меняя измеряемые элементы. Например, в треугольнике 1–2–3 в одном случае измеряют основание 1–2 и высоту 3–5, в другом – основание 1–3 и высоту 2–4. Расхождение между двумя значениями площадей не должно превосходить Вычисление площади аналитическим способом, по координатам вершин углов многоугольника, обеспечивает более высокую точность (до Расчетная формула для определения площади многоугольника (в простейшем случае треугольника – рис. 13):
Рис. 13
Произведя соответствующие алгебраические действия и преобразования, получим расчетные формулы:
где i = 1, 2, 3 ... – номера вершин полигона; При произвольных очертаниях границ участков определение площади возможно также двумя способами: графическим (палетки) и механическим (планиметры). Для определения площадей небольших участков с криволинейными контурами применяют палетки – квадратные (рис. 14) и параллельные (рис. 15).
Палетки изготавливают на прозрачном материале, расстояние между линиями 1–2 мм. Квадратная палетка применяется для малых участков, имеющих площадь на плане до 2 см2. Подсчитывают число полных клеток, доли неполных клеток учитывают на глаз. Точность измерения примерно Параллельную палетку применяют для участков, площадь которых на плане до 10 см2. Палетку на измеряемый контур накладывают так, чтобы точки 1 и 2 расположились между параллельными линиями. Тогда отрезки 3–4, 5–6 и так далее можно считать полусуммой оснований соответствующих трапеций. Найдя суммарную длину этих отрезков и умножив ее на высоту трапеции (т.е. на величину расстояния между параллельными линиями), получим площадь контура. При механическом способе применяют планиметры различных конструкций, чаще всего – полярный планиметр.
6.1. Устройство и поверки планиметра
Полярный планиметр (рис. 16) состоит из трех частей: полюсного 1 и обводного 2 рычагов и каретки счетного механизма. Полюсный рычаг с одной стороны имеет груз с иглой 3, которая является полюсом планиметра; перед началом измерений иглу вдавливают в бумагу. С другой стороны полюсный рычаг заканчивается шарниром 6, с помощью которого он соединяется с кареткой счетного механизма. На конце обводного рычага имеется обводный шпиль 7, которым обводят контур участка, удерживая рычаг за ручку 8. Для того чтобы шпиль не царапал карту, существует штифт 9, длину которого можно регулировать с помощью гайки. На обводном рычаге расположена каретка со счетным механизмом (рис. 17). Он состоит из счетного колеса 12, счетчика целых оборотов счетного колеса 13 и верньера 14. При измерении площади участка ободок счетного колеса 15 и ролик 16 должны находиться в пределах листа карты.
Рис. 16
Рис. 17
Счетное колесо разделено на 100 делений, каждые 10 делений оцифрованы. Десятые доли делений счетного колеса определяются по верньеру. Делением планиметра называется одна тысячная часть окружности счетного колеса. Отсчет по планиметру всегда состоит из четырех цифр. Первая цифра – ближайшая к указателю меньшая цифра счетчика оборотов 13, вторая и третья цифры – сотни и десятки делений на счетном колесе, предшествующих указателю верньера 14 (начальному штриху шкалы верньера, т.е. 0); четвертая цифра – номер штриха верньера, совпадающего с каким-либо штрихом счетного колеса (единицы делений). На рис. 17 отсчет по счетному механизму составляет 3578. Прежде чем приступать к измерению площади, необходимо убедиться в исправности планиметра. Он должен удовлетворять двум условиям. |
|


 .
.
 считается допустимой при самых точных измерениях расстояний (
считается допустимой при самых точных измерениях расстояний (  – 1 см на 10 км). Искажение по длине составит
– 1 см на 10 км). Искажение по длине составит . Тогда
. Тогда  . Ho
. Ho  и тогда
и тогда  . Соответственно
. Соответственно  и
и  км (с округлением до 1 км).
км (с округлением до 1 км).
 , получаем
, получаем 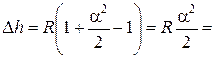
 . При разных значениях S получаем:
. При разных значениях S получаем: .
. – в числителе единица, в знаменателе степень уменьшения m,например
– в числителе единица, в знаменателе степень уменьшения m,например  (или М = 1:2000).
(или М = 1:2000). (в 1 см 50 м) расстояние между точками составляет 1,5 см. Определить горизонтальное проложение между этими же точками на местности.
(в 1 см 50 м) расстояние между точками составляет 1,5 см. Определить горизонтальное проложение между этими же точками на местности. см
см  .
. , где Т — число тысяч в знаменателе численного масштаба. Так, например, при измерении отрезков по карте М
, где Т — число тысяч в знаменателе численного масштаба. Так, например, при измерении отрезков по карте М 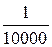 и пользовании линейным масштабом, который помещен обычно за южной стороной рамки листа карты, расхождения при двойных измерениях не должны превышать 1,5 ´ 10 = 15 м.
и пользовании линейным масштабом, который помещен обычно за южной стороной рамки листа карты, расхождения при двойных измерениях не должны превышать 1,5 ´ 10 = 15 м.
 , где п – число установок измерителя при измерении данного отрезка.
, где п – число установок измерителя при измерении данного отрезка.
 . Соответственно отрезок ef = 2cd; рq = 3сd и т. д. Если m = п = 10, то cd = 0,01 основания, т.е. такой поперечный масштаб позволяет определенным образом оценить отрезок с точностью в 0,01 доли основания, дополнительную часть этой доли – на глаз. Поперечный масштаб, у которого длина основания 2 см и m = п = 10, называют сотенным нормальным.
. Соответственно отрезок ef = 2cd; рq = 3сd и т. д. Если m = п = 10, то cd = 0,01 основания, т.е. такой поперечный масштаб позволяет определенным образом оценить отрезок с точностью в 0,01 доли основания, дополнительную часть этой доли – на глаз. Поперечный масштаб, у которого длина основания 2 см и m = п = 10, называют сотенным нормальным.
 , но dпл = 0,1 мм, тогда dместн = 2000 ´ 0,1 мм = 200 мм = 0,2 м. Следовательно, в этом масштабе (1:2000) предельная графическая точность при нанесении линий на план будет характеризоваться величиной 0,2 м, хотя линии на местности могли измеряться с более высокой точностью.
, но dпл = 0,1 мм, тогда dместн = 2000 ´ 0,1 мм = 200 мм = 0,2 м. Следовательно, в этом масштабе (1:2000) предельная графическая точность при нанесении линий на план будет характеризоваться величиной 0,2 м, хотя линии на местности могли измеряться с более высокой точностью. следует отобразить здание, длина которого в натуре 15,6 м. Определите длину здания на плане в мм.
следует отобразить здание, длина которого в натуре 15,6 м. Определите длину здания на плане в мм. ;
;  .
. . Здесь T – число тысяч в знаменателе численного масштаба.
. Здесь T – число тысяч в знаменателе численного масштаба.


 .
. ,
,
 [га], где m – знаменатель численного масштаба. Точность определения площадей примерно
[га], где m – знаменатель численного масштаба. Точность определения площадей примерно  измеряемой величины.
измеряемой величины. измеряемой величины).
измеряемой величины).
 .
.
 ;
; ,
, – номер последующей вершины;
– номер последующей вершины;  – номер предыдущей вершины.
– номер предыдущей вершины.
 .
.
