|
|
Вопрос № 3. «Элементы аналитической геометрии»Вопрос № 1. «Алгебра и начала математического анализа» 1. Понятие о степени с рациональным показателем. 2. Рациональные числа. Иррациональные числа. Понятие о мнимых и комплексных числах. 3. Логарифм. Свойства логарифмов. Основное логарифмическое тождество. 4. Десятичный и натуральный логарифмы, число e. 5. Понятие убывающей функции, пример, графическая иллюстрация. 6. Понятие возрастающей функции, пример, графическая иллюстрация. 7. Непрерывность функции. Точки разрыва. 8. Понятие о точках максимума (минимума) функции, пример, графическая иллюстрация. 9. Достаточные условия существования максимума (минимума) функции. 10. Понятие четной функции, пример, графическая иллюстрация. 11. Понятие нечетной функции, пример, иллюстрация на графике. 12. Понятие периодической функции, пример, иллюстрация на графике. 13. Схема исследования функции. 14. Понятие производной, ее геометрический и физический смысл. 15. Вторая производная. Точки перегиба. Выпуклость графика функции. 16. Степенная функция с нечетным показателем, ее свойства и график. 17. Логарифмическая функция, ее свойства и график. 18. Функция y = sin x, ее свойства и график. Доказательство одного из свойств. 19. Функция y = cos x, ее свойства и график. Доказательство одного из свойств.
20. Функция y = tgx, ее свойства и график. Доказательство одного из свойств. 21. Степенная функция с четным показателем, ее свойства и график. 22. Показательная функция, ее свойства и график. 23. Первообразная. Ее свойства. 24. Определенный интеграл, понятие, свойства. Геометрический смысл. 25. Нахождение площади криволинейной трапеции. Формула Ньютона-Лейбница. 26. Степенная функция с дробным показателем, ее свойства и график.
Вопрос № 2. «Стереометрия» 1. Основные аксиомы стереометрии. Задание плоскостей в пространстве (Теоремы) 2. Взаимное расположение прямых в пространстве. Параллельные прямые. Скрещивающиеся прямые. Угол между двумя прямыми в пространстве. 3. Параллельность прямой и плоскости (признаки). 4. Параллельность прямой и плоскости (свойства) 5. Перпендикулярность прямой и плоскости (свойства). 6. Перпендикулярность прямой и плоскости (признаки). 7. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Теорема о трех перпендикулярах. 8. Параллельность плоскостей (признаки). 9. Параллельность плоскостей (свойства). 10. Перпендикулярность плоскостей (свойства). 11. Перпендикулярность плоскостей (признаки) 12. Расстояние от точки до плоскости. 13. Расстояние между прямой и параллельной ей плоскостью. 14. Расстояние между параллельными плоскостями. 15. Призма, ее основания, боковые ребра, высота. Прямая и правильная призмы. 16. Формула площади полной поверхности призмы. Формула объема призмы. 17. Параллелепипед. Куб (определения, свойства ребер, граней). Площадь поверхности. Формулы объема прямоугольного параллелепипеда, куба. 18. Пирамида, ее основание, боковые ребра, высота. Правильная пирамида. 19. Формулы площади поверхности и объема пирамиды. 20. Правильные многогранники (тетраэдр, куб, октаэдр). 21. Цилиндр, его основания, образующая, боковая поверхность, высота. 22. Формулы площади поверхности и объема цилиндра. 23. Конус, его основание, образующая, боковая поверхность, высота. 24. Формулы площади поверхности и объема конуса. 25. Шар и сфера, их сечения. 26. Формулы объема шара и площади сферы. Вопрос № 3. «Элементы аналитической геометрии» 1. Понятие вектора. Сложение векторов. Умножение вектора на число. 2. Коллинеарные вектора. 3. Скалярное произведение векторов. Свойства. 4. Векторное произведение векторов. Свойства. 5. Угол между векторами. 6. Базис. Разложение вектора по базису. 7. Ортонормированный базис. Координаты вектора. 8. Скалярное произведение векторов, заданных своими координатами. 9. Векторное произведение векторов, заданных своими координатами. 10. Расстояние между двумя точками, заданными своими координатами. 11. Направляющий вектор прямой. 12. Нормальный вектор прямой. 13. Уравнение прямой с угловым коэффициентом. 14. Уравнение прямой в отрезках 15. Общее уравнение прямой. 16. Уравнение прямой, проходящей через две заданные точки. 17. Уравнения прямых, параллельных осям координат. 18. Уравнение прямой по точке и направляющему вектору. 19. Уравнение прямой по точке и нормальному вектору. 20. Условие параллельности прямых. 21. Условие перпендикулярности прямых. 22. Условие пересечения прямых. 23. Угол между двумя прямыми. 24. Уравнение окружности с центром в начале координат. 25. Уравнение окружности с центром в произвольной точке. 26. Сложение, вычитание, умножение на сколяр векторов, заданных своими ординатами. Практическое задание № 1. «Алгебра и начала математического анализа» 1. Найдите корень уравнения 2. Найдите корень уравнения 3. Решите неравенство 4. Решите неравенство 5. Прямая 6. На рисунке изображён график функции
7. Найти наибольшее значение функции 8. Найти наименьшее значение функции 9. Найти наибольшее значение функции 10. Найти экстремумы функции 11. Найдите первообразную 12. Вычислите интеграл 13. Вычислите интеграл 14. Вычислите интеграл 15. Вычислите интеграл 16. . Вычислите интеграл 17. Вычислите предел 18. Вычислите предел 19. Вычислите предел 20. Вычислите предел 21. Найти площадь фигуры, ограниченной параболой 22. Найти площадь фигуры, ограниченной функциями 23. Найти площадь фигуры, ограниченной функциями 24. Найти площадь фигуры, ограниченной одной полуволной графика функции 25. Найти площадь фигуры, ограниченной параболой 26. Найти площадь фигуры, ограниченной параболой Практическое задание № 2. «Стереометрия», «Элементы аналитической геометрии». 1. Вычислите периметр треугольника, вершинами которого служат точки А(6;7), В(3;3), С(1;-5). 2. Составьте уравнение прямой , проходящей через точку (-3;2) параллельно прямой 3. Составьте уравнение прямой , проходящей через точку (-2;2) перпендикулярно прямой 4. Составьте уравнение окружности с центром в точке (-1;4), проходящей через точку (3;5). 5. Найдите координаты вершин треугольника, стороны которого лежат на прямых 2x+y-6=0, x-y+4=0 и y+1=0. 6. Вычислить угол между векторами 7. Дан треугольник с вершинами в точках А(1;2), В(4;-5) и С(5;3). Вычислите его площадь. 8. Найдите вектор 9. Дан треугольник с вершинами в точках А(1;2), В(4;-5) и С(5;3). Вычислите величину угла А. 10. Точки O(0,0), 11. Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты 12. Во сколько раз объём конуса, описанного около правильной четырёхугольной пирамиды, больше объёма конуса, вписанного в эту пирамиду?
13. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
14. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
15. Объем параллелепипеда
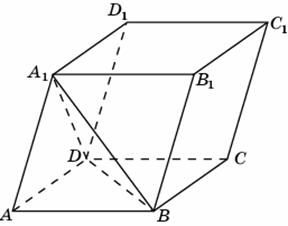
16. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
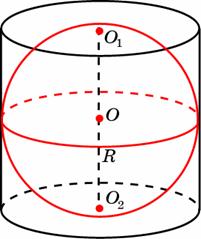
17. В цилиндрический сосуд налили 18. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 294 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 7 раз больше, чем у первого? Ответ выразите в сантиметрах. 19. Площадь большого круга шара равна 14. Найдите площадь поверхности шара. 20. Шар вписан в цилиндр. Площадь поверхности цилиндра равна 33. Найдите площадь поверхности шара.
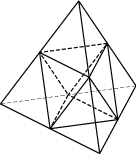
21. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в тридцать один раз? 22. Площадь поверхности тетраэдра равна 58. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
23. Диагональ куба равна 24. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60 25. Объем правильной шестиугольной пирамиды 2592. Сторона основания равна 12. Найдите боковое ребро. 26. Сторона основания правильной шестиугольной пирамиды равна 12, а угол между боковой гранью и основанием равен 45
Преподаватель _______________________________________Т. О. Сергиевская |
|
 .
. параллельна касательной к графику функции
параллельна касательной к графику функции  . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.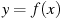 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 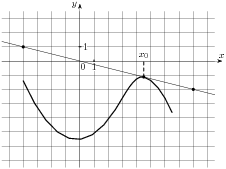
 на отрезке [-4;3]
на отрезке [-4;3]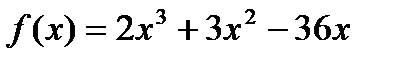 на отрезке [-2;1]
на отрезке [-2;1]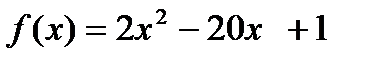
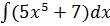
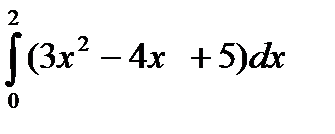
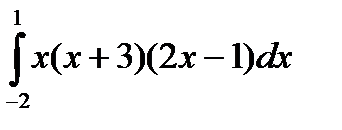
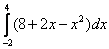
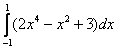
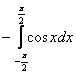
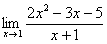
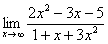

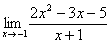
 , прямой
, прямой  и осью Ох.
и осью Ох. ,
,  и осью Ох.
и осью Ох. ,
,  и осью Ох.
и осью Ох. , расположенной над осью OX .
, расположенной над осью OX . и осью Ох.
и осью Ох. и осью Ох.
и осью Ох.
 .
. .
.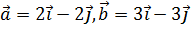
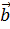 , коллинеарный
, коллинеарный  и удовлетворяющий условиям
и удовлетворяющий условиям 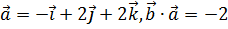
 ,
,  ,
, 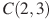 являются вершинами трапеции. Найдите длину ее средней линии DE.
являются вершинами трапеции. Найдите длину ее средней линии DE.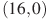 ,
,  ,
,  .
.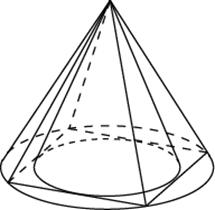
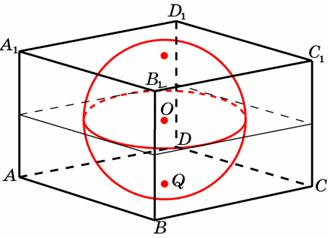
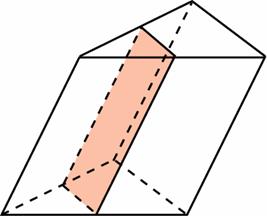
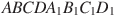 равен 9. Найдите объем треугольной пирамиды
равен 9. Найдите объем треугольной пирамиды  .
.
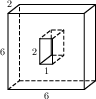
 воды. Уровень жидкости оказался равным 25 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 5 см. Чему равен объем детали? Ответ выразите в
воды. Уровень жидкости оказался равным 25 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 5 см. Чему равен объем детали? Ответ выразите в 
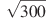 . Найдите его объем
. Найдите его объем . Высота пирамиды равна 9. Найдите объем пирамиды.
. Высота пирамиды равна 9. Найдите объем пирамиды.