|
|
Б) найти приближенное значение функции Z в точке Р,ПРОГРАММА И КОНТРОЛЬНЫЕ ЗАДАНИЯ По курсу высшей математики (для студентов экономических специальностей заочной формы обучения)
Курс первый, семестр второй
Основной формой обучения студента-заочника является самостоятельное изучение программного материала. В качестве основных пособий рекомендуются учебные пособия К выполнению контрольных работ следует приступить после самостоятельного решения достаточного количества задач по материалу, соответствующего этому заданию. В первом семестре студент должен изучить теоретический материал согласно представленной ниже программы, выполнить контрольные работы №3 и №4, защитить их в течение семестра и в сессию сдать экзамен (зачет) по курсу «Высшая математика». ПРОГРАММА КУРСА ВЫСШЕЙ МАТЕМАТИКИ ВО ВТОРОМ СЕМЕСТРЕ Раздел 1. Производная и дифференциал. 1. Определение производной, ее геометрический и механический смысл. Уравнение касательной и нормали. 2. Основные правила нахождения производных. Производная обратной и сложной функции. 3. Дифференцирование функций заданных неявно и параметрически. 4. Дифференцируемость функции. Дифференциал функции. 5. Теорема Лагранжа. Правило Лопиталя. 6. Производные и дифференциалы высших порядков. Исследование функций. 7. Условие монотонности функции. Экстремумы функции. Необходимые и достаточные условия существования экстремума. 8. Отыскание наибольшего и наименьшего значения функции, дифференцируемой на отрезке. 9. Направление выпуклости графика функции, точки перегиба 10. Асимптоты графика функции. 11. Общая схема исследования функции и построение ее графика.
Раздел 2. Дифференциальное исчисление функции нескольких переменных. 1. Функция нескольких переменных. Область определения. Предел функции. Непрерывность. 2. Частные производные. Полный дифференциал. 3. Дифференцирование сложной и неявной функций. Касательная плоскость и нормаль к поверхности. 4. Повторное дифференцирование. 5. Производная по направлению и градиент. 6. Экстремумы функции нескольких переменных. Необходимые и достаточные условия существования экстремума. 7. Условный экстремум. Метод множителей Лагранжа. Метод наименьших квадратов.
Раздел 3. Интегральное исчисление. 1. Первообразная и неопределенный интеграл, его свойства. 2. Таблица интегралов. Замена переменной и интегрирование по частям в неопределенном интеграле. 3. Стандартная техника интегрирования, использование таблиц интегралов. Интегралы, которые не выражаются через элементарные функции. 4. Определенный интеграл, теорема существования и свойства. 5. Замена переменной и интегрирование по частям в определенном интеграле. 6. Геометрические и физические приложения определенного интеграла. 7. Несобственные интегралы. Раздел 4. Дифференциальные уравнения. 1. Обыкновенные дифференциальные уравнения ( общие понятия). 2. Дифференциальные уравнения 1 порядка с разделяющимися переменными. 3. Однородные дифференциальные уравнения 1 порядка. 4. Линейные дифференциальные уравнения 1 порядка и уравнения Бернулли. 5. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и специальным видом правой части. 6. Система линейных дифференциальных уравнений с постоянными коэффициентами. КОНТРОЛЬНЫЕ ЗАДАНИЯ Общие требования В контрольную работу должны быть включены все задачи указанные в задании строго по своему варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются. При решении задач нужно руководствоваться следующими указаниями: · контрольная работа выполняется в тетради школьного типа; · контрольная работа выполняется ручкой с синей или фиолетовой пастой, с обязательным проведением полей для замечаний рецензента; · решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя и записывая номера задач; · каждое новое задание должно начинаться с новой страницы; · условие задания переписывается полностью без всяких сокращений; · графики, которые поясняют условие задачи или ее решение, должны выполняться аккуратно с применением чертежных инструментов; · решение сопровождается короткими, но исчерпывающими пояснениями; · в промежуточных вычислениях не следует вводить приближенные значения корней, чисел · при защите контрольной работы студент должен самостоятельно пояснить все решения задач и дать ответы на вопросы по теоретическому материалу, который связан с решениями; · в конце контрольной работы необходимо поставить подпись студента и дату выполнения работы. Номера задач, которые составляют задания, определяются для каждого студента индивидуально и выдаются преподавателем на установочной сессии
Задание 1. Найти производные данных функций: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Задание 2. Провести полное исследование функций и построить их графики: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Задание 3. а) найти б) найти приближенное значение функции Z в точке Р, в) написать уравнение касательной плоскости и нормали к поверхности Z в т. М0(x0, y0, z0), если P0(x0, y0) задана. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Задание 4. Исследовать на экстремум функцию 1. 4. 7. 10. 13. 16. 19. 22. 25. 28. Задание 5. Найти неопределенные интегралы 1. а) г) 2. а) г) 3. а) г) 4. а) г) 5. а) г) 6. а) г) 7. а) г) 8. а) г) 9. а) г) 10. а) г) 11. а) г) 12. а) г) 13. а) г) 14. а) г) 15. а) г) 16. а) г) 17. а) г) 18. а) г) 19. а) г) 20. а) г) 21. а) г) 22. а) г) 23. а) г) 24. а) г) 25. а) г) 26. а) г) 27. а) г) 28. а) г) 29. а) г) 30. а) г) Задание 6. 12 |
|
 . В пособиях
. В пособиях  имеется большое число задач, с которыми студенту нужно познакомиться при изучении соответствующего материала.
имеется большое число задач, с которыми студенту нужно познакомиться при изучении соответствующего материала. и
и  , а также смешанные дроби;
, а также смешанные дроби;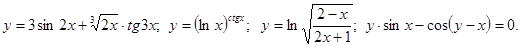
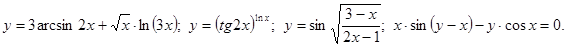

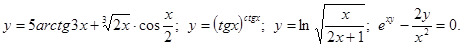
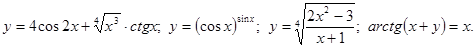
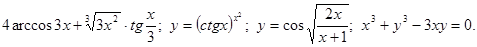
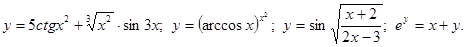
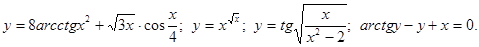
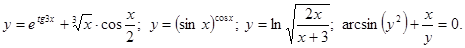
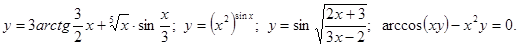
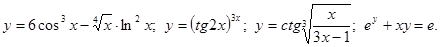
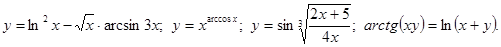
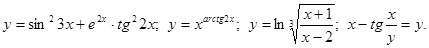
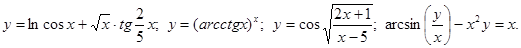
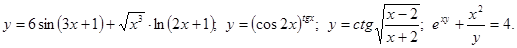
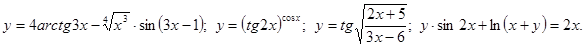
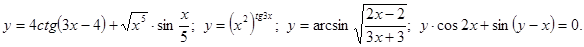
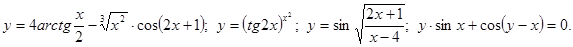
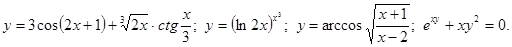
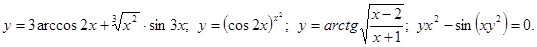
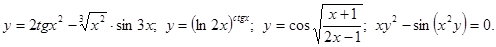
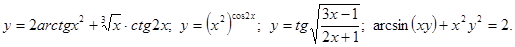
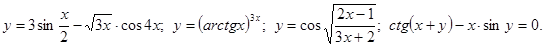
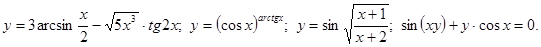
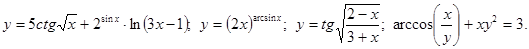
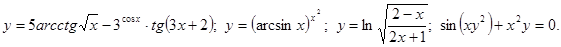
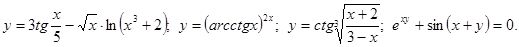
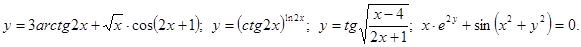
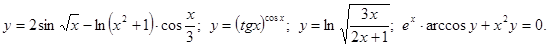
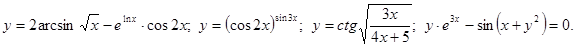
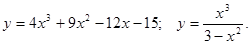
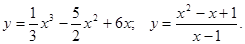
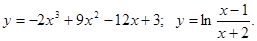
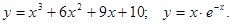
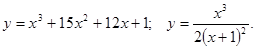
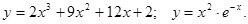
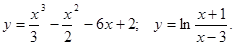
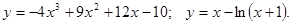
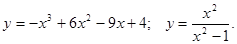
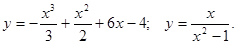

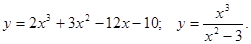
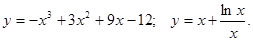
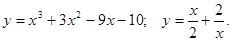
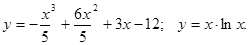
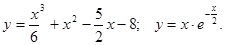
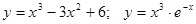 .
.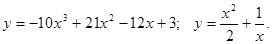
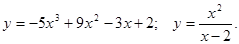
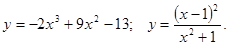
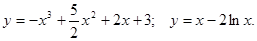
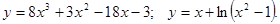



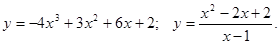
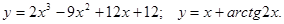

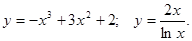
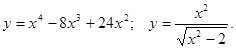
 ,
, .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.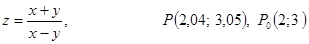 .
.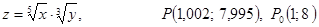 .
.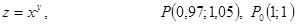
 .
.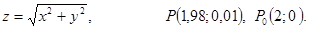

 .
.
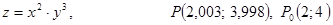 .
.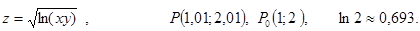
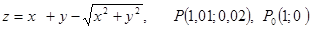 .
. .
. .
.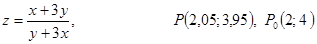 .
. .
. .
. .
. .
. .
. .
. .
. 2.
2. 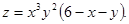 3.
3. 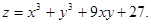
 5.
5.  6.
6. 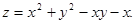
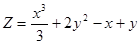 . 8.
. 8.  . 9.
. 9. 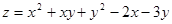
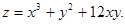 11.
11.  12.
12. 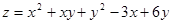
 14
14  15.
15. 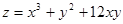
 17.
17.  18.
18. 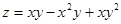 .
. 20.
20. 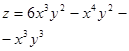 21.
21. 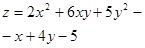
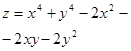 23.
23. 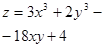 24.
24.  .
. 26.
26.  . 27.
. 27. 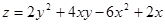
 29.
29.  30.
30. 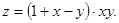
 б)
б)  в)
в) 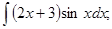
 д)
д) 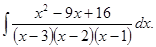
 б)
б)  в)
в) 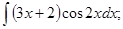
 д)
д) 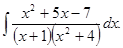
 б)
б)  в)
в) 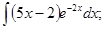
 д)
д) 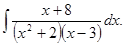

 ; б)
; б)  в)
в) 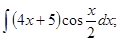
 д)
д) 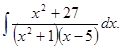
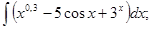 б)
б)  в)
в) 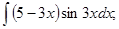
 д)
д) 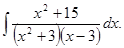
 б)
б)  в)
в) 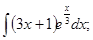
 д)
д) 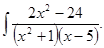
 б)
б)  в)
в) 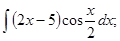
 д)
д) 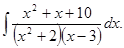
 б)
б)  в)
в) 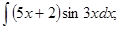
 д)
д) 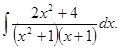
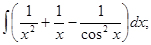 б)
б)  в)
в) 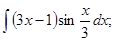
 д)
д) 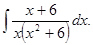
 б)
б)  в)
в) 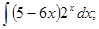
 д)
д) 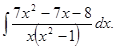
 б)
б) 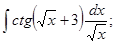 в)
в) 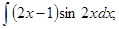
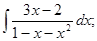 д)
д) 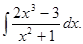
 б)
б)  в)
в) 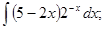
 д)
д) 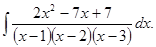
 б)
б)  в)
в) 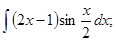
 д)
д) 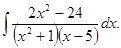
 б)
б)  в)
в) 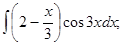
 д)
д) 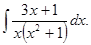
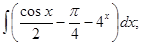 б)
б)  в)
в) 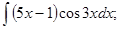
 д)
д) 
 б)
б)  в)
в) 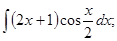
 д)
д) 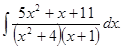
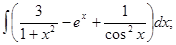 б)
б) 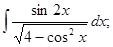 в)
в) 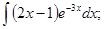
 д)
д) 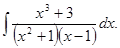
 б)
б)  в)
в) 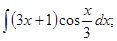
 д)
д) 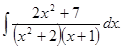
 б)
б)  в)
в) 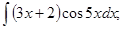
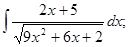 д)
д) 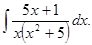
 б)
б) 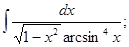 в)
в) 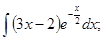
 д)
д) 
 б)
б) 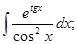 в)
в) 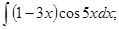
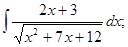 д)
д) 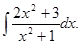
 б)
б)  в)
в) 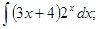
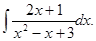
 б)
б)  в)
в) 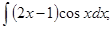

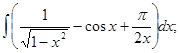 б)
б)  в)
в) 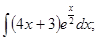
 д)
д) 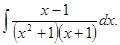
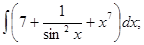 б)
б)  в)
в)  д)
д) 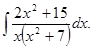
 б)
б)  в)
в) 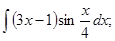
 д)
д) 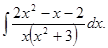
 б)
б)  в)
в) 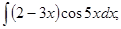
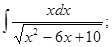 д)
д) 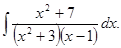
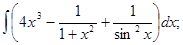 б)
б) 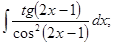 в)
в) 
 д)
д) 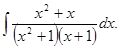
 б)
б)  в)
в) 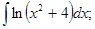
 д)
д) 
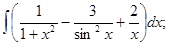 б)
б)  в)
в) 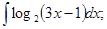
 д)
д) 