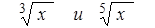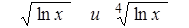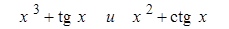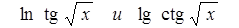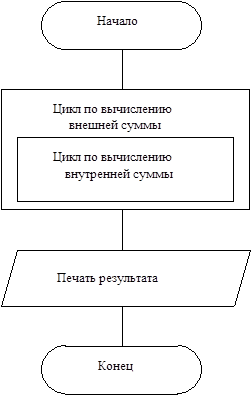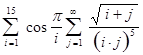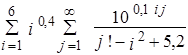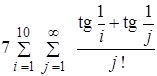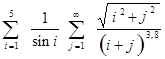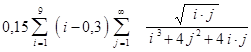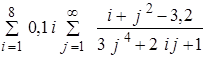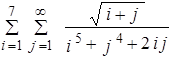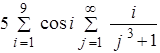|
|
Циклы с заранее неизвестным числом повторенийЦелью работы является освоение программирования алгоритмов с циклической структурой и выхода из цикла по условию, не зависящему от количества циклов. Примером такой задачи является вычисление суммы с бесконечным верхним пределом. Проверка цикла осуществляется следующим образом. Так как выражение под знаком суммы постепенно убывает с ростом слагаемых в сумме, то наступает момент, когда очередное слагаемое станет меньше наперед заданного числа (грубо говоря, точности вычисления сумм), и остальные слагаемые будут мало влиять на конечный результат. Поэтому, когда выражение под знаком суммы Так как количество слагаемых заранее неизвестно, то циклом FOR пользоваться нельзя. Для этих целей предназначаются циклические операторы WHILE и REPEAT. Необходимо помнить, что у них параметр цикла автоматически не изменяется и его надо менять принудительно. Поэтому при составлении блок-схемы алгоритма блок "Модификация" не используется. При вычислении суммы должен вычисляться факториал по формуле:
Где П знак произведения (аналогично знаку суммы), то есть 5! = 12345 = 120. Факториал можно вычислить отдельным циклом, а можно и в цикле вычисления суммы. Для этого вводится дополнительная переменная, например f = j !, и затем в цикле умножается на текущее значение j. Кроме значения суммы на печать полезно вывести значение счетчика циклов, то есть узнать, из скольких слагаемых состоит сумма. Примечание. В языке Турбо Паскаль под переменные типа INTEGER выделяется два байта, и допустимые для них значения находятся в диапазоне только от -32768 до 32767. Поэтому число 10!, реально равное 3628800, в этом случае будет представлено как 24320.Таким образом выражение под знаком суммы может никогда и не стать меньше заданной точности. Для работы с большими целыми числами рекомендуется использовать вещественный тип REAL с диапазоном представления от Варианты заданий
ЛабораторнаЯ работа № 5 Средства вывода. Таблицы При выводе больших объемов информации для удобства чтения ее необходимо оформлять в виде таблиц или графиков. Целью работы является изучение операторов ввода-вывода, вывод чисел в заданном виде и с определенной точностью, вывод последовательности чисел, оформленных в виде таблиц. Таблица состоит из заголовка, в котором указано, что, в каком столбце расположено, и непосредственно таблицы набора значений выводимых переменных. При выводе заголовка таблицы используется текстовая информация. Поэтому, чтобы правильно напечаталась таблица, необходимо сделать ее макет. Макет таблицы рисуется на бумаге в клетку, и каждая клетка принимается за одну позицию. При этом учитывается, где расположена таблица, т.е. сколько позиций надо отступить от левого края листа, каким образом проводятся вертикальные и горизонтальные линии (обычно вертикальные набор знаков I или !, горизонтальные знаки минус). Определяется ширина таблицы, которая зависит от количества выводимых значений и точности, с какой эти значения выводятся (длина числа зависит от количества цифр в числе). После этого, символ за символом, в операторы вывода заносится с макета информация о том, как должен выглядеть заголовок таблицы. Далее следует обычный циклический процесс с выводом в каждом цикле строки таблицы с рассчитанными значениями величин. Здесь оператор вывода наряду с текстовой информацией (вертикальная черта и пробелы), будет содержать и числовые значения. После вывода таблицы ее необходимо подчеркнуть, то есть вывести заключительную горизонтальную линию, состоящую из набора знаков минус. Пример. Вывести таблицу значений функции Блок-схема алгоритма представлена на рис 5.1, полученный результат на рис.5.2.
Рис.5.1. Блок-схема алгоритма для примера. - - - - - - - - - - - - - - - - - I X I S Q R T ( X ) I - - - - - - - - - - - - - - - - - I 2 I 1 . 4 1 4 2 1 3 2 I I 3 I 1 . 7 3 2 0 5 0 9 I I 4 I 2 . 0 0 0 0 0 0 0 I I 5 I 2 . 2 3 6 0 6 7 8 I I 6 I 2 . 4 4 9 4 8 9 6 I I 7 I 2 . 6 4 5 7 5 1 0 I I 8 I 2 . 8 2 8 4 2 7 3 I I 9 I 3 . 0 0 0 0 0 0 0 I I 1 0 I 3 . 1 6 2 2 7 7 2 I - - - - - - - - - - - - - - - - - Рис.5.2.Распечатка результата счета по программе для вывода таблиц. Варианты заданий
ЛабораторнаЯ работа № 6 Двойные и кратные циклы Целью работы является освоение программирования алгоритмов с двумя вложенными циклами. Примером такой задачи является вычисление двойной суммы, для которой укрупненная блок-схема алгоритма представлена на рисунке 6.1. Пример: вычислить с точностью до 0.001.
Здесь внешней суммой является сумма по i, а внутренней сумма по j. Можно рассматривать вычисление этих сумм отдельно, учитывая что вычисление внутренней суммы является частью вычисления внешней суммы, то есть телом внешнего цикла.
Рис.6.1. Укрупненная блок-схема алгоритма вычисления двойной суммы. Варианты заданий
ЛабораторнаЯ работа № 7 |
|
 будет меньше , то вычисления прекращаются и предполагается, что сумма найдена с заданной точностью.
будет меньше , то вычисления прекращаются и предполагается, что сумма найдена с заданной точностью.
 до
до  , или целый тип LongInt с диапазоном от -2.147.483.648 до 2.147.483.647.
, или целый тип LongInt с диапазоном от -2.147.483.648 до 2.147.483.647.
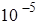

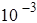

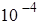



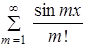




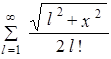










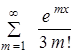
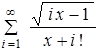

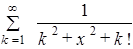




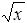 с точностью 7 знаков после запятой, причем Х изменяется от 2 до 10 с шагом 1.
с точностью 7 знаков после запятой, причем Х изменяется от 2 до 10 с шагом 1.