|
|
Раздел 3. Электрические цепи переменного токаРаздел 2. Электрические цепи постоянного тока
Задача №3 Найти сопротивление между точками А и D, приведенной на рисунке электрической схемы, если каждое из трех сопротивлений равно 1 Ом.(Сопротивлением соединительных проводов пренебречь).
Решение: Так как точки А и С, а также точки В и D соединены проводниками, сопротивление которых мы не учитываем, то схему представленную в условии задачи можно заменить эквивалентной схемой.
Из нее видно, что сопротивление между точками А и D можно вычислить по формуле для параллельного соединения проводников.
Откуда R
Ответ: Сопротивление между точками А и D равно R
Задача №4 U = Считая, что показания приборов не содержат погрешностей (ошибки исключены с помощью поправок), подсчитать мощность, выделяющуюся в сопротивлении RH. Найти погрешность измерения мощности.
Решение:
Мощность, выделяющаяся в сопротивлении Rн , подсчитанная по показаниям приборов, Риз = UI = 120 ∙ 12 = 1440 Вт, Действительное значение этой мощности Р = I Абсолютная погрешность измерения ΔP = Риз - Р = 1440 — 1425,6 = 14,4 Вт. Относительная погрешность измерения δ = ΔP/Р = 14,4/1425,6 = 0,0101 ≈ 1%. Таким образом, проведя измерение абсолютно точными приборами, получаем значение мощности, на 1 % отличающееся от действительного. Такая погрешность, вызванная самой схемой измерения, называется систематической или методической. Эта погрешность может быть найдена и непосредственно по известной формуле δ = RA / Rн Внутреннее сопротивление амперметра
RA = Погрешность
δ = RA / Rн = 0,1/9,9 = 0,0101.
Ответ: Погрешность измерения мощности δ = 0,0101 ≈ 1%.
Задача №5 Для изготовления обмотки нагревательного прибора при напряжении 220 В и токе 2 А применяется нихромовая лента. Определить длину ленты, приняв допустимую плотность тока δ = 10 нихрома= 1,1 Решение: S = Сопротивление обмотки: r= Определяем длину ленты: l = Ответ: Длина нихромовой ленты равна 20 м. Задача №6 Определить сопротивление медного провода линии передачи сечением S = 95мм ρмеди= 0,0175 αмеди = 0,004 Решение: r так как ρ задано как раз для температуры 20° С, то, подставляя значения lи S, находим: r Сопротивление провода при 0° С r Ответ: Сопротивление медного провода линии передачи сечением S = 95мм
Задача №7
Определить напряжение на выходе делителя напряжения, который подключен к источнику питания 10 В в следующих случаях: а) напряжение снимается со всего делителя напряжения; б) напряжения снимается с половины витков делителя напряжения; в) напряжение снимается с 1/4 витков делителя напряжения.
Решение:
Напряжение на выходе делителя определяется по формуле: U С другой стороны, ток переменного резистора находится из соотношения I = Следовательно, отношение напряжения на выходе делителя и напряжения питания пропорционально отношению сопротивлений R и R U Отсюда находим искомые значения напряжений на выходе делителя а) U б) U в) U Ответ: а) напряжение снимается со всего делителя напряжения U б) напряжения снимается с половины витков делителя напряжения U в) напряжение снимается с 1/4 витков делителя напряжения U
Задача №8
Определять токи и напряжения в электрической цепи, изображенной на рисунке, при следующих ее данных: Е = 2 в; r
Решение:
Находим проводимость параллельно соединенных ветвей gАБ = g2 откуда следует, что сопротивление этого участка r общее сопротивление всей цепи r = r Ток в неразветвленной части цепи I Напряжение между точками АБ U Токи в отдельных ветвях I I I Ответ: токи и напряжения в электрической цепи равны: U I I I I
Задача №9
При разомкнутом ключе К показания вольтметра 2,1 В. Когда ключ замкнут, амперметр фиксирует ток 1А. Внешнее сопротивление цепи R = 2 Ом. Определить ЭДС источника Е, внутреннее сопротивление источника R
Решение:
Когда цепь тока разорвана, вольтметр, подключенный к зажимам источника, практически фиксирует значение ЭДС. Следовательно, E = 2,1 В. Для определения R I = Откуда R
Так как известно, что внешнее сопротивление цепи R= 2 Ом, то внутренне сопротивление источника R Напряжение на зажимах источника U = E - R или U = RI Подставляя значения в приведенные выражения, получим U = 2,1 – 0,1 • 1 = 2 B; U = 2 • 1 = 2В; Применение формулы U = E - R
Ответ: E = 2,1 В. R U = 2 B;
Задача №10
Для электрической цепи представленной на рисунке, методом двух узлов, определить токи во всех ее ветвях. Задачу решить в общем виде, учесть, что известны следующие параметры электрической цепи: E1, E2, Ri1, Ri2,R1, R2, R3.
Решение:
Решение данной задачи состоит в расчете сложной цепи переменного тока методом двух узлов. Для этого надо применительно к представленной на рисунке электрической схеме: 1) выбрать направления всех токов одинаковыми 2) найти проводимости всех ветвей, См, G1 =
G2 =
G3 =
3) определить узловое напряжение Uab
Uab =
(E2G2 - со знаком "минус", так как E2 имеет противоположное I2направление);
I1 = (E1 – UAB)G1
I2 = (-E2 – UAB)G2
I3 = (0 – UAB)G3
Задача №11
Генератор постоянного тока с параллельным возбуждением работает на нагрузку, сопротивление которой Rн = 5 Ом, сопротивление обмотки якоря Rя = 0,2 Ом, сопротивление обмотки возбуждения RB=230 Ом, напряжение на зажимах генератора U =230 В. Определить: а)ЭДС генератора; б) электромагнитную мощность; в) потери мощности в обмотках якоря и возбуждения?
Решение:
Токи нагрузки
Iн = U/Rн = 230/5 = 46А
возбуждения
Iв = U/Rв = 230/230 = 1А
Якоря Iя = Iн + Iв = 46 + 1 = 47A
ЭДС генератора
Е = U + Iя ∙ Rя = 230+47 ∙ 0,2 = 239,4 В
Электромагнитная мощность
Pэ = Е ∙ Iя = 239,4 ∙ 47 = 11251,8 Вт.
Потери мощности в меди обмотки якоря Рмя = Iя
Потери мощности в меди обмотки возбуждения Рмв = Iв
Добавочные потери в соответствие ГОСТом составляют 1 % от полезной мощности генератора Рдоб = 0,01 UIн = 0,01 ∙ 230 ∙ 46 = 105,8 Вт
Потери в щеточных контактах
Рк = 2ΔUIя = 2 ∙ 0,5 ∙ 47 = 47 Вт
Ответ: ЭДС генератора Е = 239,4 В; электромагнитную мощность Pэ = 11251,8 Вт; потери мощности в обмотках якоря Рмя = 441,8 Вт и возбуждения Рмв = 230 Вт.
Задача №12
Чему равны одинаковые электрические токи, протекающие в двух параллельных проводах, которые расположены на расстоянии, а = 20 смдруг от друга, если на каждый метр провода действует сила F μ Для воздуха μ
Решение:
I
Ответ: Электрические токи, протекающие в двух параллельных проводах, которые расположены на расстоянии, а = 20 см равны 10000А.
Задача №13
Три конденсатора, емкости которых С
Решение:
Записываем формулу для определения общей емкости трехпоследовательно соединенных конденсаторов.
C Ответ: Общая емкость трех конденсаторов, соединенных последовательно равна 8,13 мкф.
Задача №14 Определите емкость батареи конденсаторов, если емкость первого конденсатора С
Решение:
Конденсаторы С C Конденсатор C
C
Ответ: C
Задача №15
Три одинаковых конденсатора соединены параллельно в батарею. Определите емкость батареи, если известно, что при подключении аккумулятора (U = 2 В) на обкладках каждого конденсатора накапливается заряд, равный 10
Решение:
При параллельном соединении конденсаторов имеем: C = C U = U Следовательно, С = 3 C т. к. C
Ответ: Емкость батареи конденсаторов равна С = 1,5 • 10
Задача №16
Три конденсатора С
Решение:
Записываем формулу для определения общей емкости трех параллельносоединенных конденсаторов. Но, так как, емкость всех трех конденсаторов одинакова то, можно воспользоваться, более простой формулой. С
Ответ: Общая емкость трех конденсаторов, соединенных параллельно равна 6 мкф.
Задача №17
Пространство между плоскопараллельными металлическими пластинам заполнено парафинированной бумагой. Определить допустимое и пробивное напряжения между пластинами при условии, что допустимое напряжение должно быть меньше пробивного в 2,5 раза. Расстояние между пластинами d = 0,I мм. εпр = 104
Решение:
Пробивное напряжение: U пр = ε пр • d =104 • 0,1 = 1000 в. Допустимое напряжение
Ответ: Пробивное напряжение между пластинами равно 1000 в. Допустимое напряжение по условию задачи должно быть меньше пробивного в 2,5 раза и равно 400 в.
Раздел 3. Электрические цепи переменного тока
Задача №18
Электротехническое устройство с потребляемой мощностью 50 Вт и напряжением питания 110 В нужно включить в сеть переменного напряжения 220 В частотой 50 Гц. Найти емкость конденсатора, который необходимо подключить последовательно данному устройству, чтобы скомпенсировать избыточное напряжение.
Решение:
Для решения задачи необходимо определить ток и напряжение компенсирующего конденсатора, что позволит найти его реактивное сопротивление, а следовательно, и емкость. Поэтому ток в цепи не должен превышать I = Напряжение на конденсаторе должно быть равно векторной разности напряжений питания и нагрузки: U Зная напряжение и ток конденсатора, находим его реактивное сопротивление: Х По известной формуле для определения емкостного сопротивления X находим искомую емкость конденсатора С =
Ответ: Емкость конденсатора, который необходимо подключить последовательно данному устройству, чтобы скомпенсировать избыточное напряжение С = 7,6 мкФ.
Задача №19
В электрическую цепь переменного тока напряжением U = 220В, частотой f = 50Гц включена катушка с индуктивностью L = 0,0127Гн и активным сопротивлением R Определить: 1) реактивное сопротивление катушки; 2) ток в катушке; 3) активную мощность катушки; 4) реактивную мощность катушки; 5) энергию, запасаемую в магнитном поле катушки.
Решение:
X Z = I = P = U Sin φ = Q = UI sinφ = 220 • 44 • 0,8 = 7744 Вар; W
Ответ: X Z = 5 Oм; I = 44A; P = 5808 Вт; Sin φ = 0,8; Q = 7744 Вар; W
Задача №20
К генератору переменного электрического тока с напряжением U = 240В и частотой f = 50Гц присоединен конденсатор с емкостью C = 40 мкф. Определить: 1) реактивное сопротивление емкости X 2) ток в электрической цепи; 3) реактивную мощность цепи Q 4) максимальную энергию, запасаемую в электрическом поле конденсатора W
Решение:
X I = Q W
Ответ: Реактивное сопротивление емкости X Ток в электрической цепи I = 3 A; Реактивная мощность цепи Q Максимальная энергия, запасаемая вэлектрическом поле конденсатора W
Задача №21
В электрическую цепь переменного тока напряжением U = 220 В, частотой f = 50 Гц включена катушка с индуктивностью L = 25,5 мГн и активным сопротивлением R Определить: X
Решение:
X Z = I = U U Cos φ =
Ответ: X Z = 10 Oм; I = 22 A; U U Cos φ = 0,6.
Задача №22
В электрическую сеть напряжением 220В включено 16одинаковых электрических ламп мощностью по 100Вткаждая. Определить необходимое сечение медного провода, соединяющего эти электрические лампочки.
Площадь поперечного сечения Наиболее допустимый медного провода, мм 0,50 10 0,75 13 1,0 15
Решение: Полная мощность Р = P ламп • 16 = 100 • 16 = 1600 Вт. Ток в проводе I = По таблице, приведенной в условии задачи, выбираем сечение провода; S = 0,50 мм
Ответ: Сечение медного провода, необходимое для подключения 16одинаковых электрических ламп мощностью по 100Вт каждая в электрическую сеть напряжением 220В равно 0,50 мм
Задача №23
Генератор переменного тока, используемый для получения переменной электродвижущей силы, имеет частоту вращения 2800 об/мин. Определить частоту, период и угловую частоту электрического тока, возникающего при подключении генератора к нагрузке, если число пар полюсов генератора равно 6.
Решение:
Частота электрического тока генератора
f = pn/60 = 6 ∙ 2800/60 = 280 Гц.
Период Т= 1 / f = 1/280 = 0,0036 с
и угловая частота
ω = 2π/Т = 2 π f = 2 ∙ 3,14 ∙ 280 = 1750 1/с. Ответ: Частота электрического тока равна f = 280 Гц, период электрического тока равен Т= 0,0036 с, угловая частота электрического тока равна ω = 1750 1/с.
Задача №24
В электрическую цепь переменного тока напряжением U = 220 В, частотой f = 50 Гц включена катушка с индуктивностью L = 25,5 мГн и активным сопротивлением R Определить: 1) максимальную мощность в активном сопротивлении P 2) активную мощность; 3) реактивную мощность; 4) полную мощность.
Решение:
P P = UI cos φ = 220 • 22 • 0,6 = 2904 Вт. Q = UI sin φ =220 • 22 • 0,8 = 3872 Вар. S = UI = 220 • 22 = 4840 BA.
Ответ: P P = 2904 Вт. Q = 3872 Вар. S = 4840 BA.
Задача №25
Лампа накаливания включена параллельно с линейным резистором R2 = 30 Ом.
Построить зависимость эквивалентного сопротивления Rэк цепи от напряжения U на его зажимах. Методом последовательных приближений определить напряжение U при токе в неразветвленной части цепи I = 5А. Вольт-амперная характеристика лампы задана в таблице. U, B I, A 0,6 1,1 1,5 1,85 2,15 2,4
Решение:
Построим вольт-амперные характеристики элементов цепи.
На рисунке: I(U) — характеристика лампы и I2(U) — характеристика резистора R2. Сложив ординаты этих характеристик при различных значениях напряжения, получим вольт-амперную характеристику всей цепи, т. е. зависимость тока в неразветвленной части цепи от приложенного напряжения I(U). Эквивалентное сопротивление схемы найдем как отношение Rэк = U/I для различных значений приложенного напряжения. Результаты вычислений приведены на графике представленном на рисунке.
|
|


 =
=  +
+  +
+  =
=  ;
; =
=  =
= 
 0,33 Ом.
0,33 Ом. = Мощность, потребляемая нагрузочным сопротивлением RH = 9,9 Ом, измеряется с помощью вольтметра и амперметра. Вольтметр показывает 120В, амперметр 12А.
= Мощность, потребляемая нагрузочным сопротивлением RH = 9,9 Ом, измеряется с помощью вольтметра и амперметра. Вольтметр показывает 120В, амперметр 12А.
 ∙ Rн = 122 ∙ 9,9 = 1425,6 Вт.
∙ Rн = 122 ∙ 9,9 = 1425,6 Вт. - Rн =
- Rн =  - 9,9 = 0,1 Ом
- 9,9 = 0,1 Ом :
: - удельное сопротивление нихрома.
- удельное сопротивление нихрома. =
=  = 0,2 мм
= 0,2 мм  = 110 ом.
= 110 ом. =
=  = 20 м.
= 20 м. - температурный коэффициент меди.
- температурный коэффициент меди. = ρ•
= ρ•  ;
; = 21,7 ом.
= 21,7 ом. = r
= r  =21,7 + 21,7 • 0,004 (-20
=21,7 + 21,7 • 0,004 (-20  C) = 20 ом.
C) = 20 ом.
 = I • R
= I • R
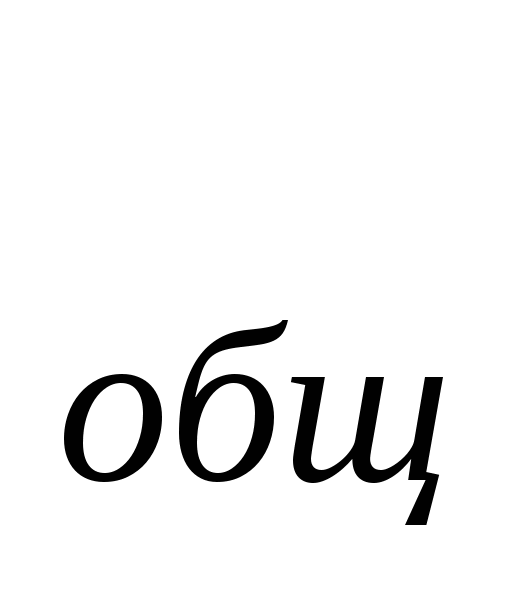 т.е.
т.е. • U
• U 
 = 10 В;
= 10 В; = 5 В;
= 5 В; = 2,5 В.
= 2,5 В. = 0,5 ом; r
= 0,5 ом; r  = 100 ом; r
= 100 ом; r  =25 ом.
=25 ом.
 + g3 + g4 =
+ g3 + g4 =  +
+  +
+  = 0,25
= 0,25  ,
, =
=  = 4 ом.
= 4 ом. =
=  = 0,25 А.
= 0,25 А. =
=  =
=  =
=  и напряжение на зажимах источника U.
и напряжение на зажимах источника U.
 ,
, =
=  = 2,1 Ом.
= 2,1 Ом.





 - магнитная постоянная.
- магнитная постоянная. =
=  = 10000А.
= 10000А. =
= 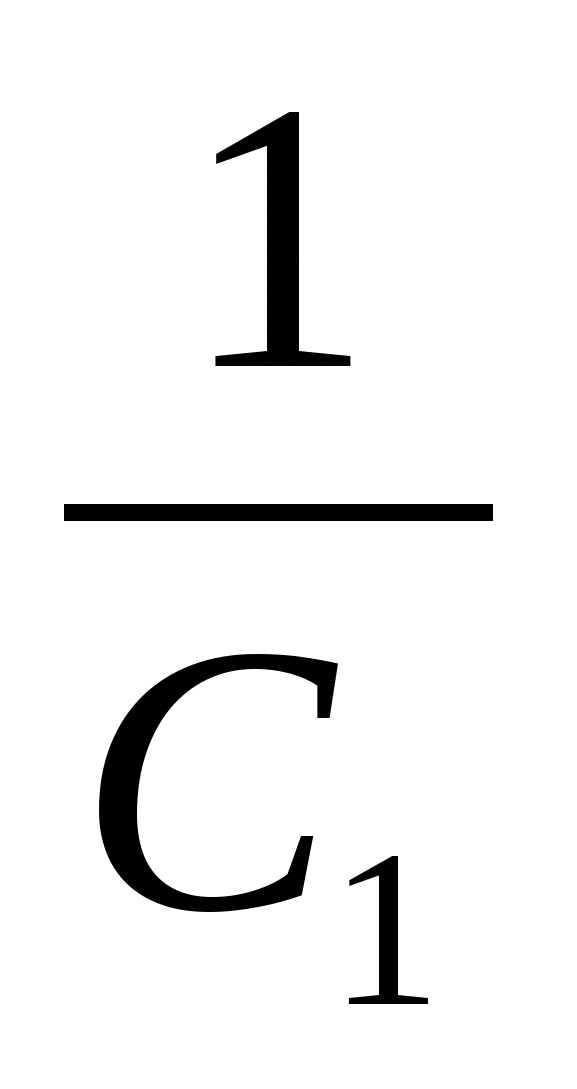 +
+  +
+  =
=  +
+  =0,05 + 0,04 + 0,033 = 0,123.
=0,05 + 0,04 + 0,033 = 0,123. = 8,13 мкф.
= 8,13 мкф.
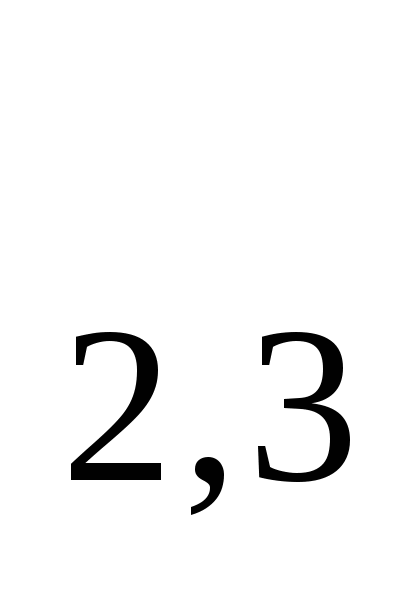 = С
= С  ;
; =
=  =
=  =
=  = 0,86 мкф.
= 0,86 мкф. Кл.
Кл.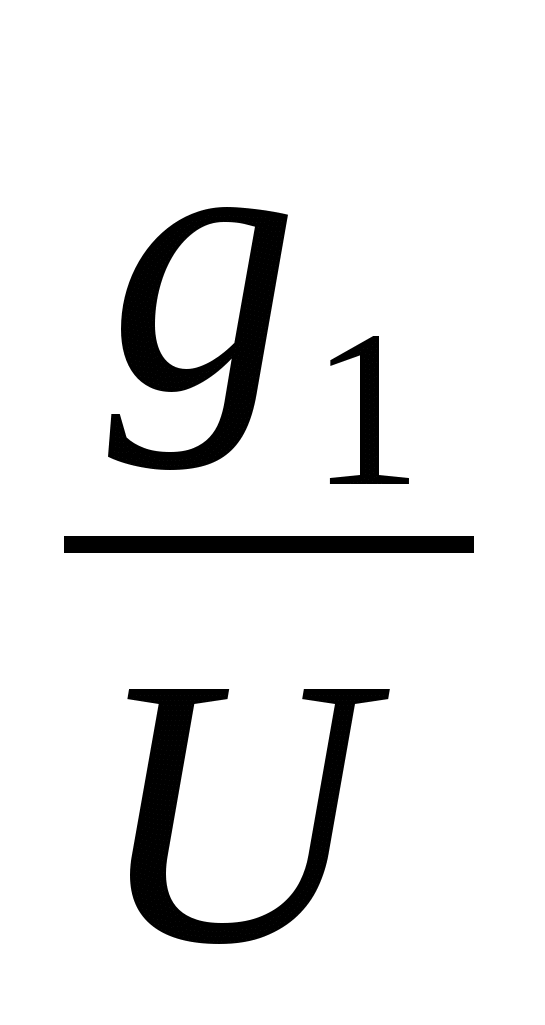 ,
, = 1,5 • 10
= 1,5 • 10  = 3 • 2 = 6 мкф.
= 3 • 2 = 6 мкф. – пробивная напряженность парафинированной бумаги.
– пробивная напряженность парафинированной бумаги. = 400 в.
= 400 в. =
=  = 0,455 A.
= 0,455 A. =
=  =
= 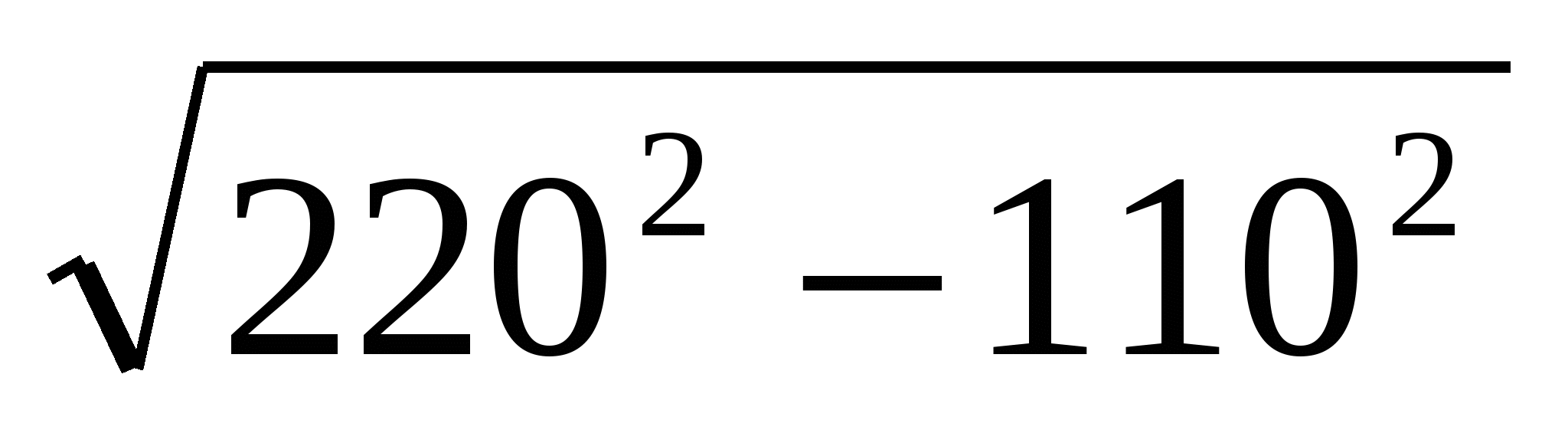 = 191 В.
= 191 В. =
=  = 420 Ом.
= 420 Ом. ;
; =
=  = 7,6 • 10
= 7,6 • 10 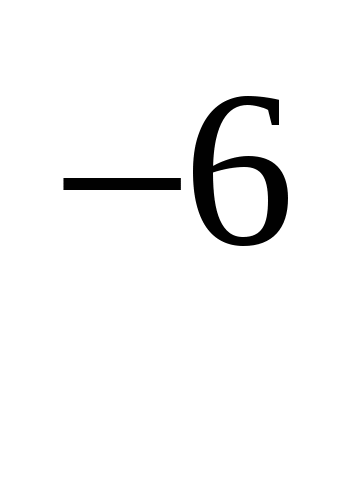 Ф = 7,6 мкФ.
Ф = 7,6 мкФ.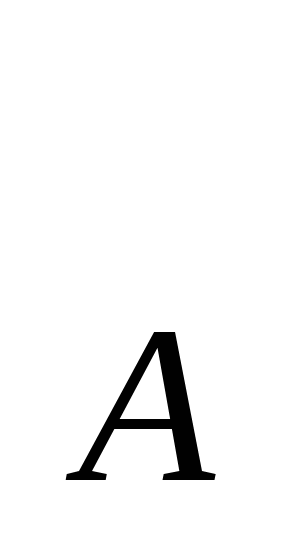 = 3Ом.
= 3Ом. = ωL = 2
= ωL = 2  fL = 2 • 3,14 • 50 • 0,0127 = 4 Oм;
fL = 2 • 3,14 • 50 • 0,0127 = 4 Oм;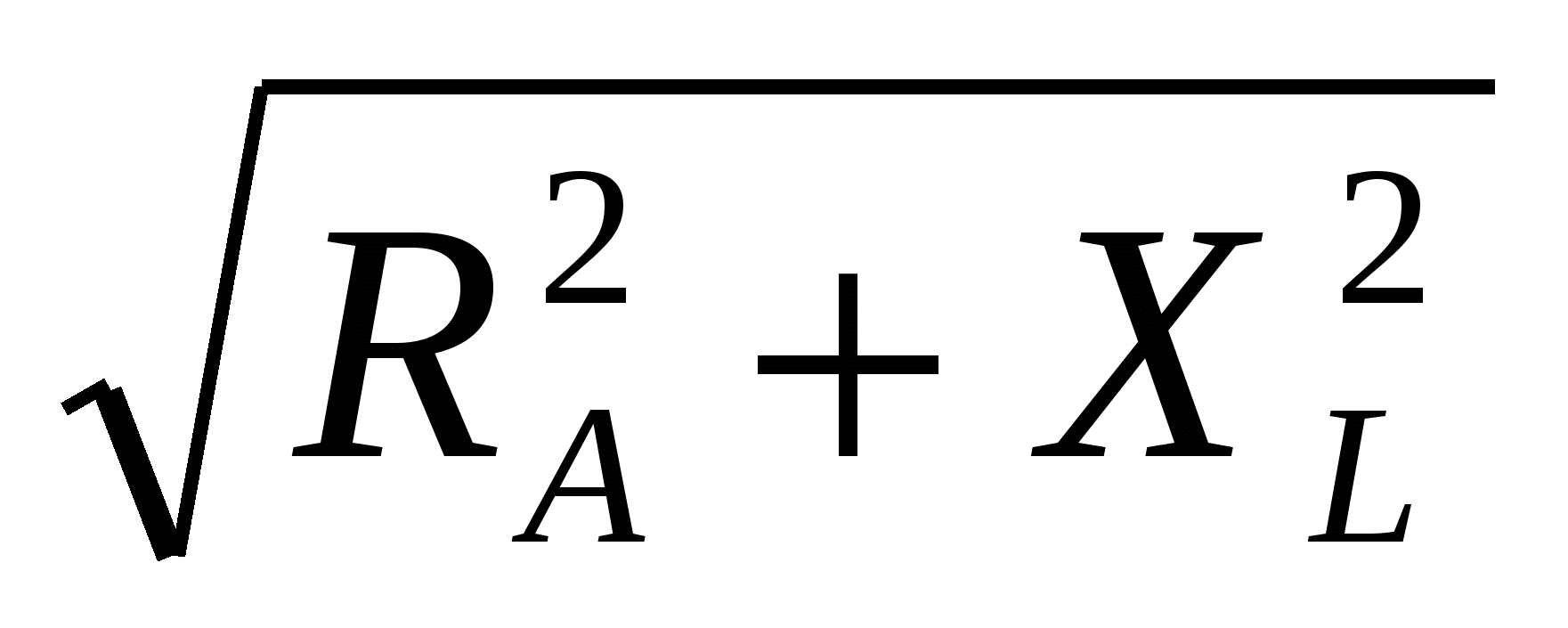 =
=  =5 Oм;
=5 Oм; =
=  = 44A;
= 44A; =
=  = 0,8;
= 0,8; = LI
= LI  .
. =
= 
 = 80 Ом.
= 80 Ом. =
=  = 3 A.
= 3 A. ; cosφ.
; cosφ. = 2 • 3,14 • 50 • 0,0255 = 8 Oм;
= 2 • 3,14 • 50 • 0,0255 = 8 Oм;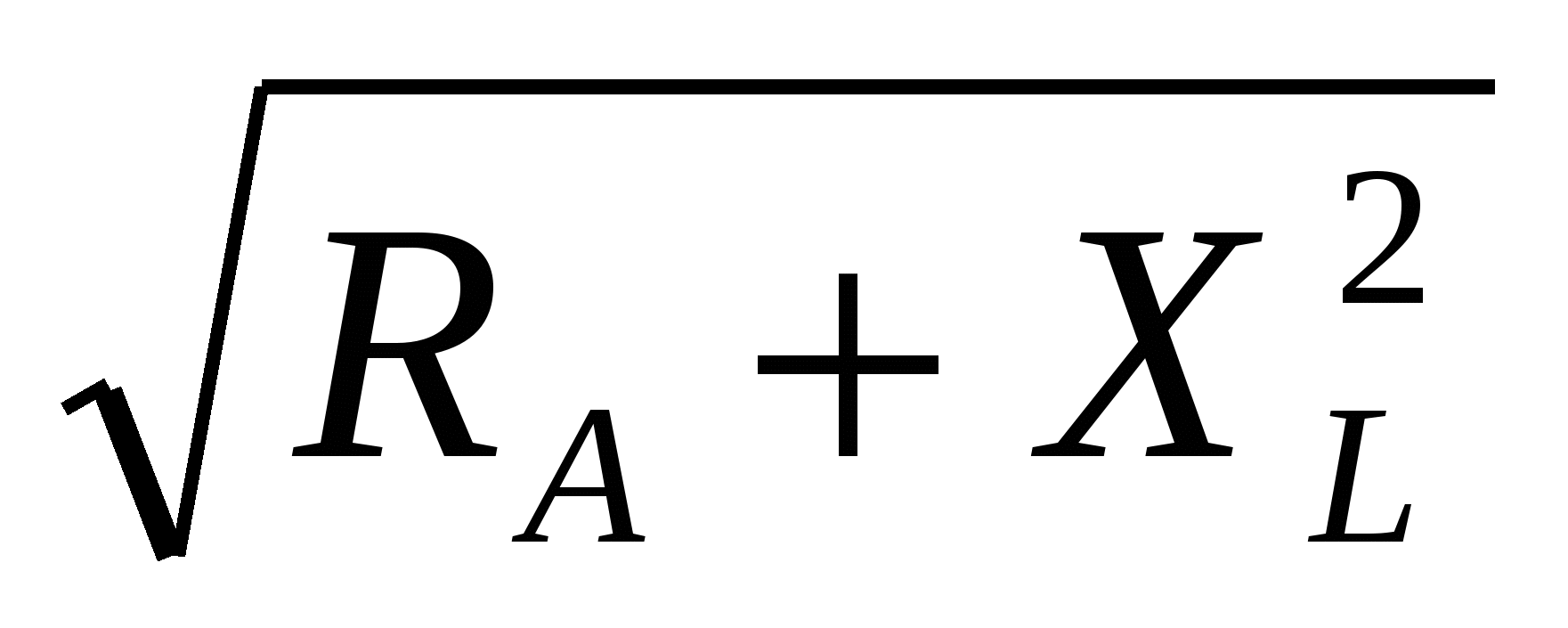 =
=  = 10 Oм;
= 10 Oм; = 22 A;
= 22 A; =
=  = 0,6.
= 0,6. =
=  = 7,273 А.
= 7,273 А. ;
;
