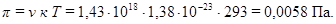|
|
Равновесное давление Р, Па 300 2500 6800 12000 25000ХИМИЯ, Ч.2 Типовые задачи с решениями Физическая химия Пример 1Рассчитать тепловые эффекты двух следующих реакций: а) б) если известны стандартные теплоты образования всех компонентов данных реакций. Решение: Выполним расчеты для 250С и давления 1 атм, приняв условие постоянства давления в ходе реакций. В этом случае тепловой эффект должен быть равен изменению энтальпии системы: а) б) Следует помнить, что все исходные для расчетов величины берутся из справочников по физико-химическим свойствам веществ. Стандартная энтальпия образования простых веществ, находящихся в наиболее устойчивой в стандартных условиях аллотропной модификации, принята равной нулю. Пример 2. Рассчитать тепловой эффект полиморфного превращения 1 моля графита в алмаз при стандартных условиях, если известны стандартные теплоты сгорания графита и алмаза при Т = 298,15 К и Р = 1атм. а) б) Решение: Запишем реакцию полиморфного превращения графита в алмаз:
Расчет показывает, что
Следовательно, процесс превращения графита в алмаз при стандартных условиях (если бы он имел место) должен был бы происходить с поглощением небольшого количества тепла. Пример 3.Как изменится температура кипения воды с ростом давления, если при температуре t = 100 оС ΔНисп = 539,7 кал/г, Vпар = 1651 см3/г, Vж = 1 см3/г. Решение:
В отличие от температуры плавления, температура кипения очень сильно зависит от давления, что связано с большой величиной DV, которой сопровождаются процессы испарения и сублимации. Пример 4.Давление пара жидкости при 10 оС и 20 оС равно, соответственно, 75000 и 107390 Па. Определить молярную теплоту испарения вещества. Решение: Воспользуемся уравнением Клаузиуса – Клапейрона в виде:
где p1 = 75000 Па; p2 = 107390 Па; T1 = 273,15 + 10 = 283,15 К; T2 = 273,15 + 20 = 293,15 К; R = 8,314 Дж/(моль·К). Тогда
В отличие от теплоты парообразования, которая изменяется в широких пределах, энтропия парообразования – величина более или менее постоянная. Так, для многих неорганических и органических веществ выполняется правило Трутона:
где Тн.т.кип. – нормальная температура кипения жидкости, т.е. температура кипения при внешнем давлении, равном 1 атм. Пример 5.Определить изменение энтропии при равновесном переходе 2 кг жидкой воды в пар при P = 1,0133·105 Па. Удельная теплота испарения воды равна ΔНисп = 2260,98 кДж/кг. Решение: Жидкая вода и пар при давлении 1,0133·105 Па находятся в равновесии при температуре 373,15 К. Тогда
Пример 7.В сосуд для измерения электрической проводимости, заполненный 1/32 н СН3СООН, помещены электроды площадью S = 3·10-4 м2 на расстоянии l = 2·10-2 м друг от друга. При напряжении U = 10 В через раствор идет ток силой I = 4,3058·10-3 А при T = 298 K. Определить степень диссоциации, константу диссоциации и рН раствора, если при указанной температуре предельные подвижности ионов H+ и CH3COO– соответственно равны: Решение.
Следовательно
Константа диссоциации
Пример 8.Определить рН раствора, если при 298 К ЭДС элемента
равна 0,15 В. Стандартный потенциал хингидронного электрода при этой температуре равен 0,699 В, потенциал каломельного электрода ‑ 0,337 В. Решение:
Пример 9.За 14 дней активность Ро210 уменьшилась на 6,85 %. Определить значение константы скорости реакции первого порядка и период полураспада t1/2. Решение: Из условий задачи N1 = 0,9315·N0, поэтому
Тогда
Коллоидная химия Пример 1.Найти средний сдвиг Решение: По уравнению Стокса – Эйнштейна находим коэффициент диффузии
По уравнению Эйнштейна – Смолуховского определяем средний сдвиг частиц
Пример 2.Рассчитать осмотическое давление 0,9 % масс. гидрозоля белка сыворотки крови при 293 К. Радиус частиц 1·10-7 м, плотность раствора принять за 1000 кг/м3, плотность частиц белка 1500 кг/м3. Решение: Расчет осмотического давления проводим по уравнению Вант – Гоффа
Находим число частиц в 1 м3 раствора (то есть частичную концентрацию ν). Масса одной частицы радиуса r и плотности ρ равна
Определяем массу всех частиц белка в 1 м3 раствора. В 100 г или 100 см3 раствора содержится 0,9 г белка, следовательно, в объеме 1 м3=106 см3 масса белка равна
Таким образом, частичная концентрация равна
Осмотическое давление равно
Пример 3. Используя уравнение Лэнгмюра, вычислить адсорбцию валериановой кислоты и площадь S, приходящуюся на молекулу на поверхности раздела водный раствор-воздух при Т=340 К и концентрации С=0,003 кмоль/м3 , если известны константы уравнения Шишковского: а =18,2 · 10-3; b =20,14. Решение:По уравнению Шишковского σ = σ0 – a ln (1 + bc); после дифференцирования получим
Подстановка правой части этого уравнения в уравнение Гиббса для адсорбции приводит к выражению:
При сопоставлении этого уравнения с уравнением Ленгмюра Г = Гmaxkc/1+kc видим, что k = b = 20,14:
Гmax = a/RT = 18,2·10-3/8314·340 = 6,4·10 моль/м2;
S = 1/Гmax· NA = 1/6,4·10-9·6,02·1023 = 26·10-17м2.
Пример 4. По экспериментальным данным адсорбции СО2 на цеолите с помощью графического метода определите константы уравнения Ленгмюра: Равновесное давление Р, Па 300 2500 6800 12000 25000 Адсорбция А·103, кг/кг 30 140 152 176 191 Решение Экспериментальные данные по определению изотермы адсорбции обычно обрабатывают с помощью уравнения Ленгмюра, записанного в линейной форме: 1/А = 1/Аmax + 1/А К ·1/Р или Р/А = 1/Аmax К + Р/А . Такая линейная зависимость позволяет графически определить оба постоянных параметра: А и К. Строим изотерму адсорбции в координатах Р/А = f(P). Из графика следует, что 1/Аmax·К = 1200; tga=1/Amax=5,09. Отсюда Аmax = 197·10-3 кг/кг; К = 0,004. Пример 5. Вычислить радиус частиц гидрозоля Fe(OH)3 при температуре 290 К, вязкости среды 1,1·10-3 Па·с, если среднеквадратичный сдвиг частиц при броуновском движении за t = 10 c составил 7,4·10-6 м. Решение Из уравнения Эйнштейна-Смолуховского среднеквадратичный сдвиг частиц пропорционален. Δ2 = 2RT·t / NA·6πηr = RT·t /3NAπηr, отсюда радиус частиц r= RT · t/3NApπηΔ2. Подставив численные значения, получим r = 7,07·10-8 м. |
|
 ;
; ,
, ;
; .
. ;
;


 ,
, 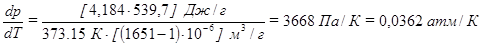 ,
,
 ,
, ,
,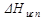 = 24720 Дж/моль.
= 24720 Дж/моль.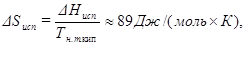

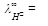 34,982·10-3 См м2 моль-экв-1,
34,982·10-3 См м2 моль-экв-1,  4,090·10-3 См м2 моль-экв-1.
4,090·10-3 См м2 моль-экв-1. ,
, 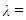 æ / C, æ
æ / C, æ  ,
, 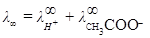 .
.

 ,
,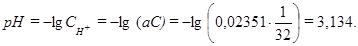
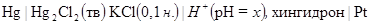

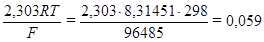 ;
;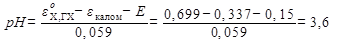 .
. дней
дней  .
. дней.
дней. при броуновском движении шарообразных частиц табачного дыма радиусом r = 10-6 м при температуре 293 К за время 10 с. Вязкость воздуха
при броуновском движении шарообразных частиц табачного дыма радиусом r = 10-6 м при температуре 293 К за время 10 с. Вязкость воздуха  Па с.
Па с.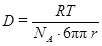 =
= 

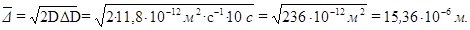
 .
.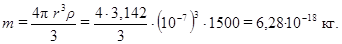

 .
.