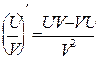|
|
ТЕМА 3:ВСТУП ДО МАТЕМАТИЧНОГО АНАЛІЗУ.29. Поняття множини, функції, послідовності. Означення функції. 30. Способи задання функції. Основні елементарні функції. 31. Нескінченно малі та нескінченно великі величини. Зв¢язок між ними. Властивості нескінченно малих величин. 32. Границя послідовності. Основні теореми про границі. Обчислення границь. 33. Границя функції. Визначені границі. Розкриття невизначеностей. 34. Неперервність функції. Властивості неперервних функцій. Точки розриву функцій та їх класифікація.
ТЕМА 4: ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ. 35. Задачі, що приводять до поняття похідної. Означення похідної. ЇЇ геометричний та механічний зміст. 36. Залежність між неперервністю та диференційованістю функцій. Правила диференціювання. 37. Похідні основних елементарних функцій. Приклади застосування похідної до розв¢язування задач з економіки. 38. Означення диференціалу функції. Правила знаходження диференціалу. 39. Диференціал складної функції. Застосування диференціалу до наближених обчислень. 40. Зростання та спадання функції. Опуклість функцій. 41. Монотонність функції. Екстремуми функції. 42. Дослідження функції та побудова графіка функції. ТЕМА 5: ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ. 43. Основні поняття та означення функції багатьох змінних. 44. Границя та неперервність функції двох змінних. 45. Частинні похідні. 46. Повний приріст функції багатьох змінних, повний диференціал. 47. Похідна за напрямком. Градієнт. 48. Застосування диференціального числення функцій багатьох змінних до наближених обчислень. 49. Поняття екстремуму функцій двох змінних. Екстремуми функції багатьох змінних. 50. Знаходження умовного екстремуму функції двох змінних методом множників Лагранжа.
ТЕМА 6: ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ 51. Первісна функції. Невизначений інтеграл. 52. Таблиця невизначених інтегралів. Безпосередне інтегрування виразів. 53. Метод підстановки та інтегрування за частинами. 54. Інтегрування раціональних дробів. 55. Інтегрування найпростіших ірраціональних функцій. 56. Означення визначеного інтегралу. Інтегральні суми. 57. Обчислення визначеного інтегралу. Формула Ньютона-Лейбніца. 58. Застосування визначених інтегралів для обчислення площ плоских фігур 59. Застосування визначених інтегралів для обчислення об¢ємів тіл обертання. 60. Основні поняття та означення диференціальних рівняннь. Задача Коші. 61. Диференціальні рівняння з відокремлюваними зміннами. 62. Диференціальні рівняння першого порядку. 63. Лінійні та однорідні диференціальні рівняння першого порядку. 64. Лінійні диференціальні рівняння зі сталими коефіцієнтами. ТЕМА 7. ЧИСЛОВІ ТА СТЕПЕНЕВІ РЯДИ. 65. Числові ряди. Основні поняття та означення. Збіжність рядів. 66. Властивості збіжних рядів. Гармонійний ряд. Необхідна умова збіжності рядів. 67. Достатні ознаки збіжності рядів: ознаки порівняння, Даламбера, Коші. 68. Знакозмінні ряди. Абсолютна та умовна збіжність. 69. Поняття функціонального ряду. Степеневі ряди. Теорема Абеля. Область збіжності степеневого ряду. 70. Розклад функції в ряд Тейлора та Маклорена. 71. Застосування рядів до наближених обчислень.
Т А Б Л И Ц Я І Н Т Е Г Р А Л І В
1.
3.
5.
7.
9. 11. 13. Формула Ньютона-Лейбніца
Т А Б Л И Ц Я П О Х І Д Н И Х 1. (xn)¢ = nxn-
3.(ax)¢ = ax lna 4. (ex)¢ = ex 5.(logax)¢ = 1/x lna 6. (lnx)¢ = 1/x 7.(cos x)¢ = - sin x 8.(sinx)′ = cosx
8.(tg x)¢=1/cos2x 9.(ctg x)¢=-1/sin2x
10. (arcsinx)=1/√1-x2 11. (arccos)′=-1/√1-x2
12. (arctgx)′=1/1+x2) 13.(arcctgx)′ = -1/1+x2 Правила диференціювання (U + V)¢ = U¢ + V¢ (UV)¢ = U¢V+V¢ U Перелік навчально-методичної літератури 1. Лейфура В. М. та ін. Математика. - К. : Техніка, 2003. - 640 с. 2. П. П. Овчинников. Вища математика. - К. : Техніка, 2000, Ч.1-2. - 1380 с. 3. М. Бугір. Математика для економістів. - Т. : Підручники, 1998.- 192 с. 4. С. М. Пастушенко. Вища математика.- К. : Діал, 2002. - 160 с. 5. Ю. К. Рудавський. математика для інженерів. - Л.: Бескид - Бід, 2002. - 262 с. 6. М. Б. Богомолов. Практичні заняття з математики. - К. : Вища математика, 1979. - 476 с. 7. Л. М. Хомченко. Вища математика. К. : Центр. Методика -інформатика, 2002.-199 с. 8. В. А. Слободская. Краткий курс висшей математики. - М. : Висшая школа, 1969. - 544с.
|
|
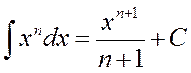 2.
2. 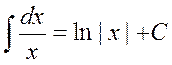
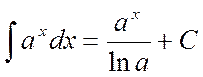 4.
4. 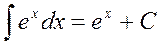
 6.
6. 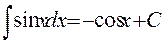
 8.
8. 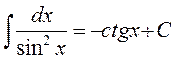
 10.
10. 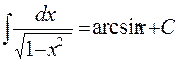
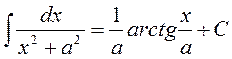 12.
12. 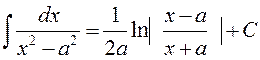
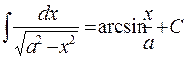
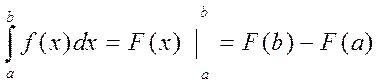
 1 2. (√x)′=1/2√x
1 2. (√x)′=1/2√x