|
|
Пояснения к рабочей программеИзучение этого раздела следует начать с элементов квантовой механики и рассмотреть такие вопросы, как корпускулярно-волновой дуализм материи, гипотезу де Бройля, уяснить, что движение любой частицы согласно этой гипотезе всегда сопровождается волновым процессом. Исходя из соотношений неопределенностей Гейзенберга, определить границы применимости классической механики и понять, что из этих соотношений вытекает необходимость описания состояния микрочастиц с помощью волновой функции, обратить внимание на ее статистический смысл. Целесообразно рассмотреть применение уравнения Шредингера к стационарным состояниям (прямоугольная потенциальная яма бесконечной глубины), следует знать правила квантования энергии, орбитального момента импульса в атоме водорода и выяснить смысл трех квантовых чисел. При изучении темы «Периодическая система элементов» необходимо обратить внимание на физический смысл спинового числа и принцип запрета Паули, на основе которого рассмотреть распределение электронов в атоме по состояниям. Переходя к изучению элементов физики атомного ядра и элементарных частиц, студент должен хорошо представлять себе состав атомного ядра и его характеристики: массу, линейные размеры, момент импульса, магнитный момент ядра, дефект массы ядра, энергию и удельную энергию связи ядра. Рассматривая состав ядра и взаимодействие нуклонов в ядре, нужно знать свойства ядерных сил и обратить внимание на их обменную природу. В процессе изучения радиоактивного распада ядер важно понять дискретный характер энергетического спектра α-частиц и γ-излучения, свидетельствующий о квантовании энергии ядер; понять закономерности β-распада, связанного с законами сохранения энергии и момента импульса. Изучая тему «Ядерные реакции», важно понять, что во всех ядерных реакциях выполняются законы сохранения: энергии, импульса, момента импульса, электрического заряда, числа нуклонов. Особое внимание уделите реакциям синтеза легких и делению тяжелых ядер, вопросам ядерной энергетики и проблемам управления термоядерными реакциями. При изучении темы «Элементы физики твердого тела» основное внимание должно быть уделено: элементам теории кристаллической решетки, элементам зонной теории твердых тел, полупроводникам, проводникам (металлам). Рассматривая эти вопросы, существенно понять характер теплового движения в твердых телах, дебаевскую теорию теплоемкости, распределение электронов по энергиям при Т=0 и Т>0, иметь качественное представление о сверхпроводимости, выяснить различие между металлами, диэлектриками и полупроводниками, рассмотреть собственную и примесную проводимости полупроводников и вольтамперную характеристику р – n -перехода. Кроме тем, затронутых в предыдущем разделе, контрольная работа № 3 представлена набором задач, включающих также следующие вопросы: определение длины волны де Бройля движущихся частиц, соотношения неопределенностей Гейзенберга, применение уравнения Шредингера для частицы, находящейся в одномерной потенциальной яме с бесконечно высокими стенками, рентгеновское излучение и закон Мозли, закон радиоактивного распада, определение дефекта массы, энергии связи и удельной энергии связи ядра, энергии ядерных реакций. В эту контрольную работу включены также задачи по теме: «Элементы физики твердого тела», в которых определяются параметры объемно-центрированных и гранецентрированных кубических решеток, удельная и молярная теплоемкости при постоянном объеме по теории Дебая при Т<<θD, примесная электропроводность некоторых полупроводников.
ОСНОВНЫЕ УРАВНЕНИЯ И ФОРМУЛЫ Длина волны де Бройля: где h – постоянная Планка, р – импульс частицы. Соотношение неопределенностей Гейзенберга для координаты и импульса: где ∆х – неопределенность координаты частицы, ∆р – неопределенность проекции импульса частицы насоответствующую координатную ось. Соотношение неопределенностей Гейзенберга для энергии и времени: где ∆E – неопределенность энергии частицы в некотором состоянии, ∆t – время нахождения частицы в этом состоянии. Плотность вероятности нахождения частицы в соответствующем месте пространства: где ψ – волновая функция частицы. Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме: где l – ширина ямы, х – координата частицы в яме (0<x<l), n – квантовое число (n=1,2,3,….). Энергия частицы в бесконечно глубокой одномерной потенциальной яме: где m – масса частицы. Серийные формулы спектра водородоподобных атомов: где λ – длина волны спектральной линии, R – постоянная Ридберга, Z – порядковый номер элемента, n=1,2,3,… k = n+1, n+2,… . Спектральные линии характеристического рентгеновского излучения:
где а – постоянная экранирования. Дефект массы ядра: где mp – масса протона, mп – масса нейтрона, mн – масса атома водорода Энергия связи ядра: Удельная энергия связи: Закон радиоактивного распада: где N0 – начальное число радиоактивных ядер в момент времени t=0, N – число нераспавшихся радиоактивных ядер в момент времени t, λ – постоянная радиоактивного распада. Активность радиоактивного вещества: Закон поглощения гамма-излучения веществом: где Iо – интенсивность гамма-излучения на входе в поглощающий слой вещества, I – интенсивность гамма-излучения после прохождения поглощающего слоя вещества толщиной х, μ – линейный коэффициент поглощения. Энергия ядерной реакции: где m1 и m2 – массы покоя частиц, вступающих в реакцию, Среднее число фононов с энергией εi в кристалле: где k – постоянная Больцмана, Т – термодинамическая температура. Молярная изохорная теплоемкость кристаллической решетки при температуре Т<< θD: при температуре Т >> θD: θD – характеристическая температура Дебая. Среднее число свободных электронов с энергией Еi в металле: где ЕF – энергия Ферми. Примесная электропроводность полупроводников:
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить дебройлевскую длину волны протона. Решение. Длина волны де Бройля λ определяется по формуле: Так как по условию задачи: то кинетическая энергия Т протона сравнима с его энергией покоя ео, импульс р и кинетическая энергия связаны релятивистским соотношением: Подставляя в (3) условие (2), найдем: Учитывая равенство (4), запишем (1) в виде: Подставляя в (5) числовые значения, получим: Ответ: λ =1,77·10-15 м. 2. Масса движущегося электрона в три раза больше его массы покоя. Чему равна минимальная неопределенность координаты электрона? Решение.Используя соотношению неопределенностей Гейзенбергаможно записать: Ответ: 3. Среднее время жизни атома в возбужденном состоянии составляет 10 нс. Вычислить естественную ширину спектральной линии (λ=0,7мкм), соответствующую переходу между возбужденными уровнями атома. Решение. При переходе электрона из одного стационарного состояния в другое излучается (или поглощается) энергия, равная: где Еn и Еk – энергетические уровни атома, соответствующие h– му и k– му уровням, λ – длина волны излучения. Из (1) следует, что неопределенность длины волны ∆λ излучения связана с неопределенностью энергии уровней ∆Еn и ∆Еk атома соотношением: Согласно соотношению неопределенностей Гейзенберга:
Из (2) с учетом (3) найдем минимальную неопределенность длины волны излучения, которая называется естественной шириной спектральной линии: Если одно из состояний, между которыми совершается переход, является основным, то: Ответ: 4. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности. Решение. Волновая функция ψ, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной l, имеет вид: Ответ: 5. Длина волны линии Lα вольфрама равна 0,148 нм. Найти постоянную экранирования. Решение. В соответствии с законом Мозли: Ответ: 6. Вычислить дефект массы, энергию связи и удельную энергию связи ядра Решение. Дефект массы ∆m ядра определяется по формуле: Ответ: 7. Сколько атомов распадается в 1г трития Решение. Перепишем закон радиоактивного распада, учитывая, что среднее время жизни радиоактивного изотопа t находится как: Ответ: 8. На поверхность воды падает гамма-излучение с длиной волны 0,414 пм. На какой глубине интенсивность излучения уменьшится в два раза?
Ответ: 9. Вычислить энергию ядерной реакции: Решение. Энергия ядерной реакции определяется по формуле: Ответ: Q=-17,3 МэВ. 10. Полоний имеет простую кубическую решетку. Постоянная решетки равна 0,334 нм. Вычислить плотность полония. Решение. Плотность полония можно вычислить по формуле:
Обозначения решеток: ПК – простая кубическая; ОЦК – объемоцентрированная кубическая; ГЦК – гранепентрированная кубическая. Из таблицы следует, что для простой кубической решетки: Ответ: 11. Молярная изохорная теплоемкость аргона при температуре 4 К равна 0,174 Дж/моль∙К. Определить значение молярной изохорной теплоемкости аргона при температуре 2К. Решение. Согласно теории Дебая, теплоемкость кристаллической решетки при низких температурах Т, когда Т<<θD (квантовая область), где θD – характеристическая температура Дебая, пропорциональна кубу термодинамической температуры: Ответ: 12. Дебаевская температура кристалла равна 150 К. Определить максимальную частоту колебаний кристаллической решетки. Сколько фононов такой частоты возбуждается в среднем в кристалле при температуре 300 К? Решение.Дебаевская температура: Ответ: КОНТРОЛЬНАЯ РАБОТА № 3
301. В вакууме распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны 0,1 А/м. Определить амплитуду напряженности электрического поля волны и среднюю по времени плотность энергии волны. 302. В однородной и изотропной среде 303. Уравнение плоской электромагнитной волны, распространяющейся в среде с 304. В вакууме распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны 100 В/м. Какую энергию переносит эта волна через площадку 50 см2 , расположенную перпендикулярно направлению распространения волны, за время t = 1 мин. Период волны Т<<t. 305. В среде 306. Уравнение плоской волны, распространяющейся в упругой среде, имеет вид 307. Колеблющиеся точки удалены от источника колебаний на расстояние 0,5 и 1,77 м в направлении распространения волны. Разность фаз их колебаний равна 3π/4. Частота колебании источника 100 с-1. Определить длину волны и скорость ее распространения. 308. Чему равна разность фаз колебаний двух точек, если они удалены друг от друга на расстояние 3 м и лежат на прямой, перпендикулярной фронту волны. Скорость распространения волны 600 м/с, а период колебаний 0,02 с. 309. Определить длину звуковой волны в воздухе при температуре 20°С, если частота колебаний 700 Гц. 310. Найти скорость распространения звука в двухатомном газе, если известно, что плотность этого газа при давлении 105 Па равна 1,29 кг/м3. 311. Расстояние между двумя когерентными источниками 0,9 мм, а расстояние от источников до экрана 1,5 м. Источники испускают монохроматический свет с длиной волны 0,6 мкм. Определить число интерференционных полос, приходящихся на 1 см экрана. 312. В опыте Юнга одна из щелей перекрывалась прозрачной пластинкой толщиной 11 мкм, вследствие чего центральная светлая полоса смещалась в положение, первоначально занятое десятой светлой полосой. Найти показатель преломления пластины, если длина волны света равна 0,55 мкм. 313. На мыльную пленку падает белый свет под углом 45°. При какой наименьшей толщине пленки отраженные лучи будут окрашены в зеленый цвет (λ=0,54 мкм)? Показатель преломления мыльной воды 1,33. 314. На пленку из глицерина толщиной 0,25 мкм падает белый свет. Каким будет казаться цвет пленки в отраженном свете, если угол падения лучей равен 60°? 315. Для устранения отражения света на поверхность стеклянной линзы наносится пленка вещества с показателем преломления 1,3 меньшим, чем у стекла. При какой наименьшей толщине этой пленки отражение света с длиной волны 0,48 мкм не будет наблюдаться, если угол падения лучей 30°? 316. На тонкий стеклянный клин падает нормально свет с длиной волны 0,72 мкм. Расстояние между соседними интерференционными полосами в отраженном свете равно 0,8 мм. Показатель преломления стекла 1,5. Определить угол между поверхностями клина. 317. На тонкий стеклянный клин падает нормально монохроматический свет. Наименьшая толщина клина, с которой видны интерференционные полосы в отраженном свете, равна 0,12 мкм. Расстояние между полосами 0,6 мм. Найти угол между поверхностями клина и длину волны света, если показатель преломления стекла 1,5. 318. Кольца Ньютона образуются между плоским стеклом и линзой с радиусом кривизны 10 м. Монохроматический свет падает нормально. Диаметр третьего светлого кольца в отраженном свете равен 8 мм. Найти длину волны падающего света. 319. Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. Длина волны света 0,5 мкм. Найти радиус кривизны линзы, если диаметр четвертого темного кольца в отраженном свете равен 8 мм. 320. В установке для наблюдения колец Ньютона пространство между линзой и стеклянной пластинкой заполнено жидкостью. Определить показатель преломления жидкости, если диаметр второго светлого кольца в отраженном свете равен 5 мм. Свет с длиной волны 0,615 мкм падает нормально. Радиус кривизны линзы 9 м. 321. Под каким углом к горизонту должно находиться Солнце, чтобы его лучи, отраженные от поверхности воды, были максимально поляризованы? 322.Естественный свет падает на кристалл алмаза под углом полной поляризации. Найти угол преломления света. 323. Естественный свет падает на поверхность диэлектрика под углом полной поляризации. Коэффициент отражения света равен 0,085. Найти степень поляризации преломленного луча. 324. Естественный свет падает на поверхность диэлектрика под углом полной поляризации. Коэффициент пропускания света равен 0,92. Найти степень поляризации преломленного луча. 325. Естественный свет падает на поверхность диэлектрика под углом полной поляризации. Степень поляризации преломленного луча составляет 0,09. Найти коэффициент отражения света. 326. Естественный свет проходит через два поляризатора, угол между главными плоскостями которых равен 30°. Во сколько раз уменьшится интенсивность света после прохождения этой системы? Считать, что каждый поляризатор отражает и поглощает 10% падающего на них света. 327. Чему равен угол между главными плоскостями двух поляризаторов, если интенсивность света, прошедшего через них, уменьшилась в 5,3 раза? Считать, что каждый поляризатор отражает и поглощает 13% падающего на них света. 328. Естественный свет проходит через два поляризатора, угол между главными плоскостями которых 30°. Во сколько раз изменится интенсивность света, прошедшего эту систему, если угол между плоскостями поляризаторов увеличить в два раза? 329. Кварцевую пластинку толщиной 3 мм, вырезанную перпендикулярно оптической оси, поместили между двумя поляризаторами. Определить постоянную вращения кварца для красного света, если его интенсивность после прохождения этой системы максимальна, когда угол между главными плоскостями поляризаторов 45°. 330. Раствор сахара с концентрацией 0,25 г/см3 толщиной 18 см поворачивает плоскость поляризации монохроматического света на угол 30°. Другой раствор толщиной 16 см поворачивает плоскость поляризации этого же света на угол 24°. Определить концентрацию сахара во втором растворе. 331. Определить длину волны, отвечающую максимуму испускательной способности черного тела при температуре 37 °С и энергетическую светимость тела. 332. Максимум испускательной способности Солнца приходится на длину волны 0,5 мкм. Считая, что Солнце излучает как черное тело, определить температуру его поверхности и мощность излучения. 333. Считая, что Солнце излучает как черное тело, определить интенсивность солнечного излучения вблизи Земли. Температуру поверхности Солнца принять равной 5780 К. 334. Считая, что Солнце излучает как черное тело, вычислить насколько уменьшается масса Солнца за год вследствие излучения и сколько это составляет процентов. Температуру поверхности Солнца принять равной 5780 К. 335. Вычислить температуру поверхности Земли, считая ее постоянной, в предположении, что Земля как черное тело излучает столько энергии, сколько получает от Солнца. Интенсивность солнечного излучения вблизи Земли принять равной 1,37 кВт/м2. 336. Определить давление солнечных лучей нормально падающих на зеркальную поверхность. Интенсивность солнечного излучения принять равной 1,37 кВт/м2. 337. Плотность потока энергии в импульсе излучения лазера может достигать значения 10 Вт/м2. Определить давление такого излучения нормально падающего на черную поверхность. 338. Свет с длиной волны 0,5 мкм нормально падает на зеркальную поверхность и производит на нее давление 4 мкПа. Определить число фотонов, ежесекундно падающих на 1 см2 этой поверхности. 339. Давление света с длиной волны 0,6 мкм, падающего нормально на черную поверхность, равно 1 мкПа. Определить число фотонов, падающих за секунду на 1 см2 этой поверхности. 340. Давление света, нормально падающего на поверхность, равно 2 мкПа. Определить концентрацию фотонов вблизи поверхности, если длина волны света равна 0,45 мкм, а коэффициент отражения 0,5. 341. Определить максимальную скорость фотоэлектронов, вылетающих из вольфрамового электрода, освещаемого ультрафиолетовым светом с длиной волны 0,2 мкм. 342. Катод вакуумного фотоэлемента освещается светом с длиной волны 0,38 мкм. Фототок прекращается при задерживающей разности потенциалов равной 1,4 В. Найти работу выхода электронов из катода. 343. Цинковый электрод освещается монохроматическим светом. Фототок прекращается при задерживающей разности потенциалов 0,4 В. Вычислить длину волны света, применявшегося при освещении. 344. Красной границе фотоэффекта соответствует длина волны 0,332 мкм. Найти длину монохроматической световой волны, падающей на электрод, если фототок прекращается при задерживающей разности потенциалов равной 0,4 В. 345. Найти величину задерживающей разности потенциалов для фотоэлектронов, испускаемых при освещении цезиевого электрода ультрафиолетовыми лучами с длиной волны 0,3 мкм. 346. В результате комптоновского рассеяния на свободном электроне длина волны гамма-фотона увеличилась в два раза. Найти кинетическую энергию и импульс электрона отдачи, если угол рассеяния фотона равен 60°. До столкновения электрон покоился. 347. В результате комптоновского рассеяния на свободном электроне энергия гамма-фотона уменьшилась в три раза. Угол рассеяния фотона равен 60°. Найти кинетическую энергию и импульс электрона отдачи. До столкновения электрон покоился. 348. Гамма-фотон с энергией 1,02 МэВ в результате комптоновского рассеяния на свободном электроне отклонился от первоначального направления на угол 90°. Определить кинетическую энергию и импульс электрона отдачи. До столкновения электрон покоился. 349. Гамма-фотон с длиной волны 2,43 пм испытал комптоновское рассеяние на свободном электроне строго назад. Определить кинетическую энергию и импульс электрона отдачи. До столкновения электрон покоился. 350. Первоначально покоившийся свободный электрон в результате комптоновского рассеяния на нем гамма-фотона с энергией 0,51 МэВ приобрел кинетическую энергию 0,06 МэВ. Чему равен угол рассеяния фотона? 351. Среднее расстояние электрона от ядра в невозбужденном атоме водорода равно 52,9 пм. Вычислить минимальную неопределенность скорости электрона в атоме. 352. Используя соотношение неопределенностей, показать, что в ядре не могут находиться электроны. Линейные размеры ядра принять равными 5,8∙10-15 м. 353. Чему равна минимальная неопределенность координаты покоящегося электрона? 354. Вычислить минимальную неопределенность координаты покоящегося протона? 355. Кинетическая энергия протона равна его энергии покоя. Чему равна при этом минимальная неопределенность координаты протона? 356. Масса движущегося электрона в два раза больше его массы покоя. Вычислить минимальную неопределенность координаты электрона. 357. Чему равна минимальная неопределенность координаты фотона, соответствующего видимому излучению с длиной волны 0,55 мкм. 358. Среднее время жизни эта-мезона составляет 2,4×10-19 с, а его энергия покоя равна 549 МэВ. Вычислить минимальную неопределенность массы частицы. 359. Среднее время жизни возбужденного состояния атома равно 12 нс. Вычислить минимальную неопределенность длины волны λ=0,12 мкм излучения при переходе атома в основное состояние. 360. Естественная ширина спектральной линии λ=0,55 мкм, соответствующей переходу атома в основное состояние, равна 0,01 пм. Определить среднее время жизни возбужденного состояния атома. 361. Альфа-частица находится в бесконечно глубокой одномерной потенциальной яме. Чему равна ширина ямы, если минимальная энергия частицы составляет 6 МэВ. 362. Электрон находится в бесконечно глубокой одномерной потенциальной яме шириной 0,1 пм. Вычислить длину волны излучения при переходе электрона со второго на первый энергетический уровень. 363. Протон находится в бесконечно глубокой одномерной потенциальной яме шириной 0,01 пм. Вычислить длину волны излучения при переходе протона с третьего на второй энергетический уровень. 364. Атом водорода находится в бесконечно глубокой одномерной потенциальной яме шириной 0,1 м. Вычислить разность энергий соседних уровней, соответствующих средней энергии теплового движения атома при температуре 300 К. 365. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l в основном состоянии. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности. 366. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l в основном состоянии. Чему равно отношение плотности вероятности обнаружения частицы в центре ямы к классической плотности вероятности. 367. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l в первом возбужденном состоянии. В каких точках ямы плотность вероятности обнаружения частицы максимальна, а в каких минимальна. 368. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. Определить вероятность обнаружения частицы в пределах от 0 до l/3. 369. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l в основном состоянии. Найти отношение вероятностей нахождения частицы в пределах от 0 до l/3 и от l/3 до 2l/3. 370. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l. Вычислить отношение вероятностей нахождения частицы в пределах от 0 до l/4 для первого и второго энергетических уровней. 371. Вычислить дефект массы, энергию связи и удельную энергию связи дейтерия. 372. Вычислить дефект массы, энергию связи и удельную энергию связи альфа-частицы. 373. Вычислить дефект массы, энергию связи и удельную энергию связи ядра 374. Вычислить дефект массы, энергию связи и удельную энергию связи ядра 375. Вычислить дефект массы, энергию связи и удельную энергию связи ядра |
|
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, , mа и mя – масса атома и его ядра
, mа и mя – масса атома и его ядра  , Z и А – зарядовое и массовое числа.
, Z и А – зарядовое и массовое числа. .
.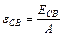 .
. ,
, .
. ,
, ,
, – сумма масс покоя частиц, образовавшихся в результате реакции.
– сумма масс покоя частиц, образовавшихся в результате реакции. ,
, ,
, ,
, ,
, , где е – элементарный заряд, n_ и n+ – концентрация электронов и дырок, b_ и b+ – подвижность электронов и дырок.
, где е – элементарный заряд, n_ и n+ – концентрация электронов и дырок, b_ и b+ – подвижность электронов и дырок. , (2)
, (2) (3).
(3). . (4)
. (4) . (5)
. (5) м.
м. .Поскольку неопределенность скорости
.Поскольку неопределенность скорости  , как и сама скорость, не может превышать скорость света с в вакууме, то:
, как и сама скорость, не может превышать скорость света с в вакууме, то:  . Так как:
. Так как: 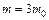 , то получим:
, то получим:  . Проводя вычисления, найдем:
. Проводя вычисления, найдем:  м.
м.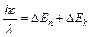 , (1)
, (1) . (2)
. (2)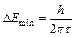 . (3)
. (3) . (4)
. (4) , поскольку для основного состояния τ = ∞. Для возбужденных состояний с одинаковым временем жизни
, поскольку для основного состояния τ = ∞. Для возбужденных состояний с одинаковым временем жизни  имеем:
имеем:  . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим:  м.
м. , где w – плотность вероятности обнаружения частицы в точке с координатой х. Если частица находится на втором энергетическом уровне, то:
, где w – плотность вероятности обнаружения частицы в точке с координатой х. Если частица находится на втором энергетическом уровне, то: 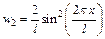 . В соответствии с принципом соответствия Бора, выражение для классической плотности вероятности получается при n→∞:
. В соответствии с принципом соответствия Бора, выражение для классической плотности вероятности получается при n→∞: 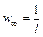 . Приравниваем по условию задачи последние два выражения и получаем:
. Приравниваем по условию задачи последние два выражения и получаем:  . Решая это уравнение, найдем:
. Решая это уравнение, найдем:  В пределах ямы (0 ≤ x ≤ l) таких точек четыре:
В пределах ямы (0 ≤ x ≤ l) таких точек четыре: 
 . Подставляя числовые данные, получаем:
. Подставляя числовые данные, получаем: 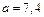 .
. .
. , или:
, или:  . Из справочных таблиц находим:
. Из справочных таблиц находим:  =1,00783 а.е.м.,
=1,00783 а.е.м.,  =1,00867 а.е.м.,
=1,00867 а.е.м.,  =15,99492 а.е.м. Подставляя числовые данные (для
=15,99492 а.е.м. Подставляя числовые данные (для  числа Z=8 и А=16), получим:
числа Z=8 и А=16), получим: 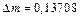 а.е.м. Энергия связи ядра ЕСВ определяется по формуле:
а.е.м. Энергия связи ядра ЕСВ определяется по формуле: 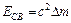 . Если дефект массы ∆m выражать в а. е. м., а энергию связи в МэВ, то:
. Если дефект массы ∆m выражать в а. е. м., а энергию связи в МэВ, то: 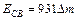 . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим:  МэВ. Удельную энергию связи εСВ находим по формуле:
МэВ. Удельную энергию связи εСВ находим по формуле:  МэВ.
МэВ. за среднее время жизни этого изотопа.
за среднее время жизни этого изотопа. , и
, и  , получим:
, получим:  . Число атомов, распавшихся за время
. Число атомов, распавшихся за время  . Найдем число атомов N0 содержащихся в массе m=1 г изотопа
. Найдем число атомов N0 содержащихся в массе m=1 г изотопа 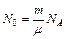 , где m=3∙10-3 кг/моль – молярная масса изотопа
, где m=3∙10-3 кг/моль – молярная масса изотопа 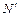 в виде:
в виде:  . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим:  .
. Решение. Из закона поглощения гамма-излучения веществом выразим х:
Решение. Из закона поглощения гамма-излучения веществом выразим х:  . Для определения коэффициента линейного ослабления вычислим энергию гамма-фотонов:
. Для определения коэффициента линейного ослабления вычислим энергию гамма-фотонов:  . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим:  =3 МэВ. По графику зависимости μ от ε (рис. 4) находим, что μ=0,04 см-1. Подставляя числовые значения в выражение для х, получим:
=3 МэВ. По графику зависимости μ от ε (рис. 4) находим, что μ=0,04 см-1. Подставляя числовые значения в выражение для х, получим: 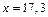 см.
см. . Выделяется или поглощается энергия при этой реакции?
. Выделяется или поглощается энергия при этой реакции? . Если массу частиц выражать в а.е.м., а энергию реакции в МэВ, то формула принимает вид:
. Если массу частиц выражать в а.е.м., а энергию реакции в МэВ, то формула принимает вид: 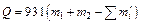 . Из справочных данных находим:
. Из справочных данных находим:  а.е.м.,
а.е.м.,  а.е.м.,
а.е.м.,  . Дефект массы реакции равен:
. Дефект массы реакции равен:  а.е.м. Подставляя значение дефекта массы реакции в выражение для
а.е.м. Подставляя значение дефекта массы реакции в выражение для  , получим:
, получим:  МэВ. Поскольку Q<0, энергия в результате реакции поглощается.
МэВ. Поскольку Q<0, энергия в результате реакции поглощается.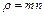 , где m – масса атома полония, n – число атомов в единице объема. Полоний имеет простую кубическую решетку. Некоторые характеристики кубических решеток приведены в следующей таблице.
, где m – масса атома полония, n – число атомов в единице объема. Полоний имеет простую кубическую решетку. Некоторые характеристики кубических решеток приведены в следующей таблице.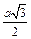

 , где а – постоянная решетки. Массу атома полония можно вычислить по формуле:
, где а – постоянная решетки. Массу атома полония можно вычислить по формуле:  . Получим:
. Получим:  . Проводя вычисления, найдем:
. Проводя вычисления, найдем:  кг/м3.
кг/м3. . При высоких температурах, когда Т >> θD (классическая область), теплоемкость кристаллической решетки описывается законом Дюлонга и Пти:
. При высоких температурах, когда Т >> θD (классическая область), теплоемкость кристаллической решетки описывается законом Дюлонга и Пти: 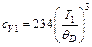 ,
,  . Отсюда:
. Отсюда:  или
или 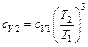 . Подставляя числовые данные, получим:
. Подставляя числовые данные, получим:  Дж/моль×К.
Дж/моль×К. , где
, где  – максимальная частота колебаний кристаллической решетки. Тогда:
– максимальная частота колебаний кристаллической решетки. Тогда:  . Подставляя числовые значения, получаем:
. Подставляя числовые значения, получаем:  Гц. Среднее число фононов с энергией εi:
Гц. Среднее число фононов с энергией εi:  . Находим:
. Находим:  .
. распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны 50 В/м. Найти амплитуду напряженности магнитного поля и фазовую скорость волны.
распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны 50 В/м. Найти амплитуду напряженности магнитного поля и фазовую скорость волны. , имеет вид:
, имеет вид:  . Определить диэлектрическую проницаемость среды и длину волны.
. Определить диэлектрическую проницаемость среды и длину волны. . Определить длину волны, скорость ее распространения и частоту колебаний,
. Определить длину волны, скорость ее распространения и частоту колебаний, .
. .
. .
.