|
|
Тема: «Кінематика прямолінійного та криволінійного руху»Розділ І. ФІЗИЧНІ ОСНОВИ МЕХАНІКИ
РІВНОЗМІННЕ ОБЕРТАННЯ
1.Колеса радіусом r = 0,1 м обертається зі сталим кутовим прискоренням ε = 3,14 рад/с2. Визначити для точок, що знаходяться на ободі колеса, в момент часу t = 1с: 1).Кутову швидкість ω; 2). Лінійну швидкість υ; 3). Тангенціальне прискорення at; нормальне прискорення аn; повне прискорення а. Обертання почалося зі стану спокою.
2.Шків обертається зі сталою швидкістю, що відповідає частоті v = 30 об/с. З деякогомоменту часу шків починає гальмувати і обертається рівноуповільнено з кутовим прискоренням ε = 3 рад/с2. За який час шків зупиниться? Скільки обертів він за цей час зробить?
3.Колесо, що обертається рівноуповільнено, зменшило свою кутову швидкість ω з 80 рад/с2 до 20 рад/с2 за 0,5 хвилини, здійснивши при цьому 60 обертів. Визначити кутове прискорення ε колеса.
4.Шків, що обертаеться рівноприскоренно, досяг кутової швидкості ω = 40 рад/с через N = 40 обертів від початку руху. Визначити кутове прискорення ε шківа.
5.Колесо, що обертається рівноуповільнено, при гальмуванні зменшило свою частоту v впродовж 2 хвилин з 600 об/хв.. до 180 об/хв. Визначити кутове прискорення ε і кількість обертів колеса за цей час.
6.Маховик за 5 хвилин від початку руху придбав швидкість, що відповідає частоті ν = 600 об/хв. Визначити кутове прискорення колеса ε та кількість обертів колеса N за цей час. Рух вважати рівноприскореним.
7.Вентилятор обертається зі швидкістю що відповідає частоті 1200 об/хв. Після відключення вентилятор, обертаючись рівноуповільнено, зробив 200 обертів. Скільки часу пройшло з моменту виключення вентилятора до його повної зупинки?
8.Колесо, що обертається рівноуповільнено, зменшило частоту обертання за 2 хвилини від 1800 об/хв.. до 900 об/хв.. Визначити кутове прискорення ε і кількість обертів N, що зробило колесо за цей час.
9. Шків, що обертається рівноуповільнено, зменшив свою частоту ν за 30 секунд від 100 до 60 об/с. Визначити кутове прискорення ε і кількість обертів, що воно зродило за цей час.
10.Махове колесо за час 2 хвилини з початку обертання, придбало швидкість, що відповідає частоті ν = 840 об/хв. Визначити кутове прискорення ε і кількість обертів, що воно зродило за цей час.
11.Точка рухається вздовж кривої зі сталим тангенціальним прискоренням аt = 0,5 м/с2. Визначити повне прискорення а на ділянці кривої радіусом кривизни r = 3 м, якщо точка рухається на цій ділянці зі швидкістю υ = 2 м/с.
НЕРІВНОЗМІННИЙ РУХ
12.Залежність відстані, що пройшло тіло, від часу описується рівнянням S(t)=2t-0.4t2+t3. Визначити в момент часу t = 2с: 1). Відстань S, що пройде тіло; 2). Швидкість υ; 3). Прискорення тіла.a
13.Рівняння швидкості тіла має вигляд: υ(t) = 0,5t + 0,01t2 + 0,02. Знайти: 1). Прискорення тіла за 10 с від початку руху; 2). Відстань, що пройде тіло за 0,5 хв. від початку руху; 3). Швидкість тіла на 5-й секунді руху.
14.Прискорення тіла характеризується рівнянням: a(t)=2+3t. Визначити відстань S, що пройде тіло, його швидкість υ та прискорення за 0,5 хв. від початку руху.
15.Залежність шляху від часу має вигляд: S(t)=10+5t+0,14t2+0,01t3. Через який час від початку руху прискорення тіла a буде дорівнювати 1 м/с2.
16.Рівняння шляху що пройшло тіло, має вигляд: S(t)=3-2t+2t2.Знайти відстань S, що пройшло тіло, його швидкість υ та прискорення тіла a через 10 с від початку руху.
17.Рівняння залежності шляху від часу має вигляд: S(t)=6-3t+2t2.Знайти відстань S, що пройде тіло, його швидкість υ та прискорення a на 5-й секунді руху.
18.Залежність швидкості матеріальної точки від часу визначається рівнянням: υ(t)=2t2+3t+5. Визначити: 1). Швидкість υ на 5-й секунді; 2). Прискорення a через 2 секунди від початку руху; 3). Переміщення тіла S через 1 хвилину від початку руху.
19.Рух матеріальної точки визначається рівнянням S(t)=100+t-0,5t2+0,1t3. Визначити: 1). Відстань S, що пройшла точка за 10 с.; 2). Швидкість υ на 3-й секунді; 3). Прискорення a на 3-й секунді від початку руху.
20.Прискорення тіла визначається рівнянням a(t)=10+0,5t. Визначити: 1). Переміщення тіла S за 2 хвилини від початку руху; 2). Швидкість тіла υ на 30-й секунді; 3). Прискорення a на 10-й секунді.
21.Залежність швидкості матеріальної точки від часу визначається рівнянням: υ(t)=0,1t2+0,5t+50. Визначити: 1). Швидкість υ на 55 секунді; 2). Прискорення a через 2 хвилини від початку руху; 3). Переміщення тіла S з 10-ї до 20-ї секунди руху.
22.Колесо, що обертається так, що залежність кута обертання радіуса колеса від часу визначається рівнянням: φ(t)=20+2t+0,2t2+0,2t3. Визначити радіус колеса, якщо відомо, що наприкінці другої секунди руху нормальне прискорення точок на ободі дорівнює an=3,46 м/с2.
23.Колесо радіусом r = 0,02 м обертається так, що залежність кута обертання радіуса колеса від часу визначається рівнянням: φ(t)=1+t+t2+t3. Для точок на ободі колеса визначити: 1). Кутову швидкість ω та лінійну швидкість υ наприкінці 10 секунди руху; 2). Кутове прискорення ε в момент часу t=2 с.; 3). Тангенціальне прискорення at, нормальне прискорення an та повне прискорення a в момент часу t= 5 с.
24.Колесо радіусом r = 0,5 м обертається так, що залежність кута обертання радіуса колеса від часу визначається рівнянням: φ(t)=100+2t2+0,1t3. Для точок на ободі колеса в момент часу t=3 с. визначити: 1). Кутову швидкість ω; 2). Лінійну швидкість υ; 3). Кутове прискорення ε; 4). Тангенціальне прискорення at, нормальне прискорення an та повне прискорення a.
25.Рух точки по колу радіусом R = 4 м задано рівнянням φ = 10 – 2t + t2. Знайти тангенціальне at, нормальне an та повне прискорення a в момент часу t = 2 с.
26.Точка рухається по колу таким чином, що залежність шляху від часу визначається рівнянням: S(t)=10+2t+t2. Визначити лінійну швидкість υ цієї точки, її тангенціальне, нормальне та повне прискорення за 3 секунди від початку руху, якщо радіус кола дорівнює r=1 м.
27.3.Залежність пройденого тілом шляху S від часу t задається рівнянням S = А+ Вt+Сt2+ Dt3, де С = 0,14 м/с2, D = 0,01 м/с3 . Через який проміжок часу після початку руху прискорення тіла буде дорівнювати 1 м/с2.
28.5. Залежність пройденого тілом шляху від часу задається рівнянням S = А – Вt2 + Ct3, (А = 2м, В = 3м/с2, С = 4м/с3 ). Знайти значення швидкості і прискорення для моменту часу t = 2 с.
29.7. Кінематичні рівняння руху двох матеріальних точок мають вид: х = А1t + В1t2 + С1t3 та x = А2t + В2t2 + С2t3, де В1 = 4 м/с2, С1 = -3 м/с3, В2 = -2 м/с2, С2 = 1 м/с3. Знайти момент часу для якого прискорення цих точок будуть однакові.
30.9. Рух матеріальної точки задано рівнянням х = Аt + Вt2, де А = 4 м/с, В = - 0,005 м/с2. Знайти момент часу, для якого швидкість точки дорівнює нулю. Знайти величину прискорення в цей момент часу.
31.11. Залежність пройденого тілом шляху від часу задається рівнянням S = Аt + 6Вt2 – 2 Сt3, де А= 4 м/с, В = 5 м/с2, С = 6 м/с3. Знайти швидкість і прискорення тіла через 2 секунди після початку руху.
32.13. Залежність пройденого тілом шляху S від часу t задається рівнянням S = А+ Вt + Сt2 +Dt3, де С = 0,28 м/с2, D = 0,02 м/с3. Через який проміжок часу пiсля початку руху прискорення тіла зросте в 4 рази?
33.15. Залежність пройденого тілом шляху від часу задається рівнянням S = А – 2 Вt2 + Сt3, (А= 20м, В = 8м/с2, С = 10м/с3). Записати вирази для швидкості і прискорення. Знайти їх значення для моменту часу t = 4 с.
34.17. Кінематичні рівняння руху двох матеріальних точок, мають вид: 35.19. Рух матеріальної точки задано рівнянням х = Аt + 2Вt2, де А = 16 м/с, В = - 0,005 м/с2. Знайти момент часу зупинки точки. Знайти величину прискорення в цей момент часу. 36.21. Залежність пройденого тілом шляху від часу задається рівнянням S = Аt + Вt2 + Сt2 , де А= 2 м/с, В = 3 м/с2, С = 4 м/с3. Знайти швидкість і прискорення тіла через 2 секунди після початку руху.
37.22. Кінематичні рівняння руху двох матеріальних точок мають вид: х1 = А1t + В1t2 + C1t3 та х2 =А2t + В2t2 + C2t3, де В1 = 4 м/с2, С1 = - 3 м/с2 , В2 = - 2 м/с2, С2 = 1 м/с3. Знайти момент часу для якого прискорення цих точок будуть однакові.
38.23. Залежність пройденого тілом шляху від часу задається рівнянням S = Аt + 6Вt2 - 2Сt3, де А = 4м/с, В = 5м/с2, С = 6м/с3. Знайти швидкість і прискорення тіла через 2 секунди після початку руху.
39.24. Залежність пройденого тілом шляху від часу задається рівнянням S = А - 2Вt2 + Сt3, (А = 20м, В = 8м/с2, С = 10м/с3). Знайти значення його швидкості і прискорення для моменту часу t = 4 c.
40.25. Рух матеріальної точки задано рівнянням x = Аt + 2Вt2, де А = 16 м/с, В = - 0,005 м/с2. Знайти момент часу зупинки точки. Знайти величину прискорення в цей момент часу.
41.28. Залежність пройденого тілом шляху S від часу t задається рівнянням S =A+Вt+Сt2+Dt3, де С = 0,1м/с2, D = 0,2м/с3 . Через який проміжок часу після початку руху прискорення тіла буде дорівнювати 2м/с2.
Тема : «Закони Ньютона»
42.2. Під дією сили F = 9,8 Н тіло рухається прямолінійно так, що залежність пройденого тілом шляху S від часу t задається рівнянням
43.4. Тіло масою 0,5 кг рухається прямолінійно, причому залежність пройденого тілом шляху S від часу t задається рівняння S = А – Вt + Сt2 – Dt3, де С = 5 м/с2, D = 1м/с3. Знайти величину сили, що діє на тіло в кінці першої секунди руху.
44.6. Тіло масою m = 3кг рухається так, що залежність пройденого шляху від часу описується рівнянням S = 5cos2πt. Записати значення сили для t = 0.
45.10. Тіло масою m =1 кг рухається прямолінійно так, що залежність пройденого тілом шляху S від часу t задається рівнянням S = А + Вt + Сt2. Знайти силу, що діє на тіло, якщо постійна С = 2 м/с2.
46.12. Під дією сили тіло масою 3кг рухається прямолінійно так, що залежність пройденого тілом шляху S від часу t задається рівнянням S = Аt3 – Вt2 + Сt + D. Знайти значення сили, яка діє на тіло через 5 с після початку руху, якщо А = 2 м/с3, В = 3 м/с2, С = 5 м/с, D = 4 м.
47.14. Тіло масою 0,5кг рухається прямолінійно, причому залежність пройденого тілом шляху S від часу t задається рівнянням S = А+ Вt + Сt2 + Dt3, де С = 1 м/с2, D = - 0,2 м/с3. Знайти величину сили, що діє на тіло в кінці другої секунди руху.
48.Тіло масою m = 1кг рухається так, що залежність пройденого шляху від часу описується рівнянням S = 20t2 – 10sin 4πt. Записати закон зміни сили від часу.
49.20. Під дією якої сили, тіло масою 10кг при прямолінійному русі, змінює пройдений шлях із часом за законом S = 10t (1 – 2t)м?
50.26. Під дією сили F = 0,5 Н тіло рухається прямолінійно так, що залежність пройденого тілом шлях S від часу t задається рівнянням S = A + Bt + Ct2. Знайти масу тіла та прискорення з яким воно рухається, якщо постійна C =2м/с2 .
51.27. Тіло масою m =2 кг рухається прямолінійно так, що залежність пройденого тілом шляху S від часу t задається рівнянням S = А + Вt + Сt2. Знайти силу, що діє на тіло, якщо постійна С = 3м/с2.
Тема «Сили інерції»
52.Судно масою m=100 т здійснює циркуляцію радіусом 0,5 км. Знайдіть силу бокового тиску судна на воду, якщо циркуляція здійснюється зі швидкістю 15 взл.
53.Трамвайний вагон масою m=6 т іде по закругленню радіусом 90 м. Визначити силу бокового тиску коліс на рельси, якщо швидкість руху υ=10,8 км/год.
54.Залізничний вагон масою 50 т рухається по закругленню радіусом 0,2 км. Визначити силу бокового тиску коліс на колію, якщо швидкість руху стає υ=36 км/год.
55.Людина масою m=70 кг знаходиться в автобусі, який здійснює поворот радіусом 10 м. З якою силою він буде притиснутий до віконного скла, якщо швидкість руху автобуса при цьому υ=18 км/год.
56.Мотоцикліст іде по горизонтальній дорозі зі швидкістю υ=72 км/год, роблячи поворот радіусом 100 м. Визначити силу бокового тиску мотоцикла на дорогу, якщо маса мотоцикліста m1=60 кг, а маса мотоцикла m2=200 кг.
57.Відерце масою m=1 кг обертається на мотузці радіусом 0,4 м у вертикальній площині. Визначити мінімальну швидкість, при якій у верхній точці вода із відерця не виливається.
58.Відерце з водою, прив’язане до мотузки довжиною 50 см, рівномірно обертається у вертикальній площині. Знайти найменшу швидкість, при якій у верхній точці із відерця не буде виливатися вода.
59.Камінь, що прив’язаний до мотузки, рівномірно обертається у вертикальній площині. Визначити довжину мотузки, якщо відомо, що швидкість обертання дорівнює υ=5 м/с.
60.Мотоцикліст їде по горизонтальній дорозі. Яку найменшу швидкість він повинен розвити, щоб, виключивши мотор, проїхати по треку, що має форму „мертвої петлі” радіусом R = 4 м? Тертям та опором повітря знехтувати.
61.Автомобіль масою 5 т рухається зі швидкістю 10 м/с по випуклому мосту. Визначити силу тиску автомобіля на міст в його верхній частині, якщо радіус кривизни моста дорівнює 50 м.
62.Акробат на мотоциклі описує „мертву петлю” радіусом 4 м. З якою мінімальною швидкістю повинен проїжджати акробат верхню точку петлі, щоб не зірватись?
63.Камінь, що прив’язаний до мотузки довжиною 0,7 м, рівномірно обертається у вертикальній площині. Визначити, якою повинна бути швидкість обертання, щоб мотузка розірвалась, якщо відомо, що вона розрахована на натяг, що відповідає п’ятикратній силі тяжіння.
64.Літак, шо рухається зі швидкістю 720 км/год виконує мертву петлю. Яким повинен бути радіус „мертвої петлі”, якщо найбільша притискуючи льотчика до сидіння сила дорівнює десятикратній силі тяжіння?
65.Літак, що рухається у повітрі зі швидкістю 1080 км/год, робить „мертву петлю”. Яким повинен бути радіус цієї петлі, щоб сила, яка притискує пілота до сидіння у верхній точці траєкторії, дорівнювала семикратній силі тяжіння?
66.Літак робить „мертву петлю” радіусом 0,9 км. З якою швидкістю виконується „мертва петля”, якщо максимальна сила, що притискує пілота до сидіння літака дорівнює п’ятикратній силі тяжіння?
67.Яку перенавантаженість буде відчувати льотчик, сидячи в кабіні літака, що виконує „мертву петлю”, якщо швидкість літака дорівнює υ=250 м/с, а радіус „мертвої петлі” 911 м?
68.На яку частину зменшиться вага тіла на екваторі Землі (у порівняння з його вагою на полюсі) внаслідок обертання Землі навколо осі, якщо радіус Землі дорівнює RЗ = = 6370 км, а період обертання T=24 години.
69.На яку частину зменшиться вага тіла на екваторі Плутона (у порівняння з його вагою на полюсі) внаслідок обертання Плутона навколо осі, якщо радіус Плутона дорівнює RП=0,3RЗ ( RЗ = 6370 км), а період обертання TП=25 діб 9 год. 36 хв.? Прискорення вільного падіння у поверхні Плутона вважати gП = 0,5 м/с2.
70.На яку частину зменшиться вага тіла на екваторі Нептуна (у порівняння з його вагою на полюсі) внаслідок обертання Нептуна навколо осі, якщо радіус Нептуна дорівнює RН=3,9RЗ ( RЗ = 6370 км), а період обертання TН=15 год. 48 хв.? Прискорення вільного падіння у поверхні Нептуна вважати gН = 14,4 м/с2.
71.На яку частину зменшиться вага тіла на екваторі Урана (у порівняння з його вагою на полюсі) внаслідок обертання Урана навколо осі, якщо радіус Урана дорівнює RУ=3,9RЗ ( RЗ = 6370 км), а період обертання TУ=10 год. 48 хв.? Прискорення вільного падіння у поверхні Урана вважати gУ = 10,4 м/с2.
72.На яку частину зменшиться вага тіла на екваторі Марса (у порівняння з його вагою на полюсі) внаслідок обертання Марса навколо осі, якщо радіус Марса дорівнює RМ=0,53RЗ ( RЗ = 6370 км), а період обертання TУ=24 год. 37 хв.? Прискорення вільного падіння у поверхні Марса вважати gМ = 3,74 м/с2.
73.На яку частину зменшиться вага тіла на екваторі Сатурна (у порівняння з його вагою на полюсі) внаслідок обертання Сатурна навколо осі, якщо радіус Сатурна дорівнює RС=9,5RЗ ( RЗ = 6370 км), а період обертання TС=10 год. 14 хв.? Прискорення вільного падіння у поверхні Сатурна вважати gС = 11,3 м/с2.
74.На яку частину зменшиться вага тіла на екваторі Юпітера (у порівняння з його вагою на полюсі) внаслідок обертання Юпітера навколо осі, якщо радіус Юпітера дорівнює RЮ=11,2RЗ ( RЗ = 6370 км), а період обертання TЮ=9 год. 50 хв.? Прискорення вільного падіння у поверхні Юпітера вважати gЮ = 25,9 м/с2.
|
|
 та
та 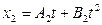 , де А1 = 4 м/с, А2 = - 8 м/с, В1 = - 4 м/с2, В2 = 2 м/с2. Знайти момент часу для якого швидкості цих точок будуть однакові.
, де А1 = 4 м/с, А2 = - 8 м/с, В1 = - 4 м/с2, В2 = 2 м/с2. Знайти момент часу для якого швидкості цих точок будуть однакові.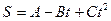 . Знайти масу тіла, якщо постійна С =1 м/с2.
. Знайти масу тіла, якщо постійна С =1 м/с2.