|
|
Теория атома водорода по Бору.Элементы квантовой механики. Основные формулы и законы · Первый постулат Бора (постулат стационарных состояний):
где · Второй постулат Бора (правило частот)
где · Обобщенная формула Бальмера, описывающая серии линий в спектре атома водорода:
где
· Радиус
где · Энергия
где · Энергия электрона в атоме водорода
где · Потенциал ионизации:
· Потенциал возбуждения:
· Длина волны де Бройля
где · Связь импульса частицы
где
Соотношение неопределенностей Гейзенберга: где · Нестационарное уравнение Шредингера:
· Уравнение Шредингера для стационарных состояний:
где · Одномерное уравнение Шредингера для стационарных состояний:
· Условие нормировки волновой функции:
· Плотность вероятности:
где · Вероятность обнаружения частицы в интервале от
· Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика шириной
где Примеры решения задач Задача 1. Определить максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера).
Подставляем числа:
Ответ:
Задача 2. Определить, на сколько изменилась энергия электрона в атоме водорода при излучении атомом фотона с длиной волны 4,86.10-7 м.
Ответ:
Контрольные задания 7.1.Атомарный водород освещается ультрафиолетовым излучением с длиной волны 100 нм. Определите, какие спектральные линии появятся в спектре излучения атомарного водорода. 7.2.Какую наименьшую энергию (в электронвольтах) должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов появились все линии всех серий спектра водорода? 7.3.Какую наименьшую скорость должны иметь эти электроны? 7.4.Максимальная длина волны спектральной линии в серии Лаймана равна 0,122 мкм. Полагая, что постоянная Ридберга неизвестна, определите максимальную длину волны в серии Бальмера. 7.5.Определите потенциал ионизации и первый потенциал возбуждения атома водорода. 7.6. Определите наибольшую и наименьшую частоты волн в серии Бальмера. 7.7.Определите наибольшую и наименьшую длины волн в серии Лаймана. 7.8.Определите кинетическую, потенциальную и полную энергии электрона на первой стационарной орбите в атоме водорода. 7.9.Определите угловую скорость электрона на первой стационарной орбите в атоме водорода. 7.10.Определите период обращения электрона на первой стационарной орбите в атоме водорода. |
|
 (
( 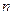 = 1, 2, 3,…),
= 1, 2, 3,…), – масса электрона;
– масса электрона;  – скорость электрона на
– скорость электрона на  ;
;  – постоянная Планка.
– постоянная Планка.
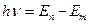 ,
,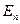 ,
,  – энергии стационарных состояний атома соответственно до и после излучения (поглощения);
– энергии стационарных состояний атома соответственно до и после излучения (поглощения); 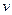 – частота излученного (поглощенного) кванта энергии.
– частота излученного (поглощенного) кванта энергии. ,
, – частота спектральных линий в спектре атома водорода;
– частота спектральных линий в спектре атома водорода;  - постоянная Ридберга;
- постоянная Ридберга; 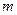 – целое число, определяет серию линий в спектре атома водорода:
– целое число, определяет серию линий в спектре атома водорода: 
 – определяет отдельные линии соответствующей серии
– определяет отдельные линии соответствующей серии 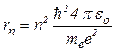 ,
, – постоянная Планка;
– постоянная Планка; – электрическая постоянная;
– электрическая постоянная;  – заряд электрона;
– заряд электрона; 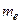 – масса электрона.
– масса электрона. ,
,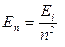 ,
,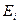 – энергия ионизации атома водорода.
– энергия ионизации атома водорода. .
.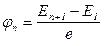 .
. ,
,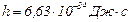 – постоянная Планка;
– постоянная Планка;  – импульс частицы (
– импульс частицы (  с ее кинетической энергией
с ее кинетической энергией  :
: ,
,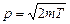 .
.
 ,
, ,
,  – соответственно неопределенности координаты, импульса, энергии и времени,
– соответственно неопределенности координаты, импульса, энергии и времени,  .
. .
. ,
, – волновая функция микрочастицы;
– волновая функция микрочастицы; 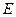 – полная энергия микрочастицы;
– полная энергия микрочастицы;  =
=  – потенциальная энергия частицы;
– потенциальная энергия частицы;  – пространственная координата (
– пространственная координата (  =
=  ); t – время, ∆=
); t – время, ∆=  – оператор Лапласа (записан в декартовых координатах);
– оператор Лапласа (записан в декартовых координатах);  – масса микрочастицы;
– масса микрочастицы;  – постоянная Планка;
– постоянная Планка;  =
=  – мнимая единица.
– мнимая единица. .
.
 .
.

 ,
, – вероятность того, что частица может быть обнаружена вблизи точки с координатой
– вероятность того, что частица может быть обнаружена вблизи точки с координатой  на участке
на участке  .
. до
до  :
: .
.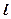 (0 ≥
(0 ≥  ≥
≥  ):
):
 (собственная нормированная волновая функция),
(собственная нормированная волновая функция),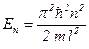 (собственное значение энергии),
(собственное значение энергии), = 0.
= 0.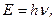 где
где 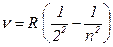 . Получаем:
. Получаем: 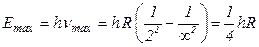 ,
,
 .
.


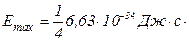
 ,
,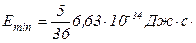
 .
.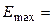
 ,
, 
 .
. где
где  - частота излучения, т.е.
- частота излучения, т.е.  . Подставляем числа:
. Подставляем числа:
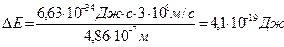 .
.


 .
.