|
|
Молекулярная физика. ТермодинамикаОсновные формулы 1. Количество вещества (число молей)[3]
где N – число молекул (атомов) вещества; 2. Молярная масса вещества
где m – масса вещества. 3. Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)
где Р, V – давление и объем газа; m – масса газа;. 4. Зависимость давления газа от концентрации молекул n и температуры (уравнение состояния идеального газа)
где k – постоянная Больцмана. 5. Концентрация молекул
6. Основное уравнение молекулярно – кинетической теории газов
где 7. Средняя кинетическая энергия поступательного движения молекулы
8. Средняя полная кинетическая энергия молекулы
где 9. Средняя квадратичная скорость молекул массой m1
10. Молярные теплоемкости тела (газа) при постоянном объеме
11. Связь между удельной
12. Уравнение Майера
13. Внутренняя энергия газа (E = U)
14. Первое начало термодинамики
где 15. Работа при расширении газа от объема V1 до объема V2 [3]
А = где 16. Работа газа при адиабатическом процессе
где γ = СP/СV – постоянная адиабаты. 17. Уравнение Пуассона при адиабатическом процессе
18. К. п. д. тепловой машины
где 19. К. п. д. идеального цикла Карно
где Примеры решения задач Пример 1. В баллоне находятся азот массой Р е ш е н и е m1 = 14 г = 14.10–3кг, Молярная масса М смеси равна отношению массы смеси m m2 = 9,0 г = 9,0.10–3кг, к количеству вещества (числу молей) ν смеси (см. (2Ф)) Т = t + 273 = 283 K, M = m/ν. (1) Р = 1,0 Мпа = 1,0.106Па. Масса смеси равна сумме масс ее компонентов
M = ? V = ? Число молей смеси равно сумме молей ее компонентов ν = где
Молярные массы азота
Учитывая (2) – (4) , найдем из (1) молярную массу смеси
Объем баллона найдем, применяя уравнение Менделеева – Клапейрона (3Ф)
откуда, используя (2) и (5),
Учитывая табличные значения универсальной газовой постоянной R и молярных масс азота V = 1,2.10–2м3 = 12 л. Пример 2. В баллоне объемом
Р е ш е н и е Применим уравнение Менделеева – Клапейрона (3Ф), к начальному (

где Искомое давление
Подставляя сюда массу
Пример 3. Найти среднюю кинетическую энергию
Р е ш е н и е
 где где  ж/К – постоянная Больцмана (находится из таблицы). Двухатомная молекула кислорода ж/К – постоянная Больцмана (находится из таблицы). Двухатомная молекула кислорода  имеет две вращательные степени свободы. Поэтому средняя кинетическая энергия вращательного движения молекулы имеет две вращательные степени свободы. Поэтому средняя кинетическая энергия вращательного движения молекулы
Кинетическая энергия вращательного движения N молекул газа
Число молекул газа
где
Пример 4. В двух теплоизолированных сосудах объемами Р е ш е н и е
где
Из сравнения первых и вторых равенств в формулах (1) и (2) имеем
Общая энергия газов в сосудах до их соединения
После смешивания газов (соединение сосудов трубкой) установится искомая температура
Число молей
Сосуды теплоизолированные, поэтому
Пример 5. Кислород массой количество теплоты, сообщенной газу.
Р е ш е н и е Используем первое начало термодинамики (14Ф)
 газа и на совершение газом работы газа и на совершение газом работы  против внешних сил. Приращение внутренней энергии (13Ф) против внешних сил. Приращение внутренней энергии (13Ф)
где
С учетом (2) и (3) количество теплоты (1) запишется
где ΔТ = Т2 – Т1. У нас процесс изобарный, поэтому температура
Тогда приращение температуры
Подставляя это выражение в (4), получим:
Учитывая условие задачи и табличные данные, найдем количество теплоты:
Пример 6. Два моля идеального газа, находящегося при температуре
Решение T1 = 300 K, Решение задачи упрощается, если заданные процессы изобразить на P1/P2 = n = 2,0, Q = ? Q = ΔU + A, (1) где
A = νRΔT = νR(T3 – T2), (2) где по условию задачи Т3 = Т1. Температура
откуда, учитывая условие задачи,
Подставляя эту формулу в уравнение (2), найдем работу, совершенную газом в данном процессе:
Приращение внутренней энергии
где
Пример 7. Объем одного моля (
Количество теплоты находится из первого начала термодинамики (14Ф) Q = ΔU + A. (1) Приращение внутренней энергии одного моля газа
где R = 8,31 Дж/(моль/.К) – универсальная газовая постоянная. Работа газа
Воспользуемся уравнением Менделеева – Клапейрона (3Ф) для одного моля газа
откуда, учитывая условие задачи,
Продифференцируем условие задачи V = а/Т
Подставляя (4) и (5) в формулу (3), найдем работу:
С учетом (2) и (6) количество теплоты (1) равно
Пример 8. Водород
Процессы расширения и сжатия газа изобразим графически в системе координат
откуда, учитывая условие задачи, получим:
где постоянная адиабаты
Учли, что молярная масса водорода
где
Подставив числовые данные, получим
В данном процессе
При изотермическом процессе Т = const и
Пример 9. У тепловой машины, работающей по циклу Карно, температура нагревателя
Р е ш е н и е
 тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя  и холодильника и холодильника  и не зависит от природы рабочего тела и устройства тепловой машины (см. (21Ф)) и не зависит от природы рабочего тела и устройства тепловой машины (см. (21Ф))
Учитывая условие задачи, получим коэффициент полезного действия машины:
К. п. д. цикла Карно можно записать также через работу
Работа
откуда с учетом (3) имеем:
Применим к изотермическому сжатию первое начало термодинамики (14Ф) в виде:
где
Пример 10. Водород совершает цикл Карно. Найти к. п. д. цикла, если при адиабатическом расширении: а) объем газа увеличивается в n = 2,0 раза; б) давление уменьшается в n = 2,0 раза.
откуда имеем
где
Подставляя это выражение в (1), найдем к. п. д. цикла Карно при увеличении объема газа в n = 2,0 раза
б) Запишем уравнение Пуассона в следующем виде:
откуда
или, учитывая условие задачи, получим:
С учетом этого выражения, из (1) найдем к. п. д. цикла, когда давление уменьшается в n = 2,0 раза
Пример 11. Один моль гелия при изобарном расширении увеличил свой объем в Р е ш е н и е
где
Приращение внутренней энергии для одного моля газа (см. (13Ф))
где Элементарная работа газа
Продифференцируем уравнение состояния идеального газа (3Ф) для одного моля
Подставляя (3) и (5) в уравнение (2), получим:
Подставим это выражение в (1) и проинтегрируем:
где
Используя это соотношение, из (6) найдем приращение энтропии:
Пример 12. Один моль двухатомного идеального газа находится при температуре Р е ш е н и е
Элементарное количество теплоты δQ = dU + δA, (2) где dU – приращение внутренней энергии, при изотермическом процессе dU = 0. Элементарная работа δА = PdV .(3) Из уравнения Менделеева–Клапейрона (3Ф), записанного для одного моля, PV = RT, найдем: P = RT/V и подставим это выражение в (3). В результате получим
Учитывая dU = 0, из (2) и (4) имеем:
Подставляя это выражение в (1), найдем приращение энтропии при изотермическом сжатии:
Учитывая условие задачи V2 = V1/2 и табличное значение универсальной газовой постоянной R = 8,31 Дж/(моль.К), получим числовое значение приращения энтропии: ΔS1 = – R Знак « минус » означает, что энтропия при этом процессе уменьшается. Это объясняется тем, что макросистема не является замкнутой. Для адиабатического процесса Температура при изотермическом процессе не изменяется, следовательно, конечная температура в этом процессе по условию задачи равна
Постоянная адиабаты
Таким образом, конечная температура больше при адиабатическом сжатии.
Таблица вариантов к контрольной работе №2
Таблица содержит варианты для специальностей, учебными планами которых предусмотрено по курсу физики четыре и шесть контрольных работ.
Количество задач и их номера указываются преподавателем.
Задачи для самостоятельного решения 201. Найти кинетическую энергию поступательного движения молекул газа, находящихся в неподвижном баллоне объемом V = 6,0 л при давлении Р = 300 кПа. 202. Найти внутреннюю энергию двухатомного газа, находящегося в сосуде объемом V = 2 л под давлением Р = 150 кПа. 203. Найти внутреннюю энергию кислорода массой m = 20 г при температуре t = 20 оС. Какая часть этой энергии приходится на долю поступательного движения молекул и какая часть – на вращательное движение? 204. Водород массой m = 0,30 г находится в сосуде объемом V = 2,0 л при давлении Р = 200 кПа. Найти среднюю квадратичную скорость и среднюю кинетическую энергию молекул водорода. 205. Найти концентрацию молекул водорода при давлении Р = 300 Па, если средняя квадратичная скорость его молекул vкв = 2,5.103 м/с. 206. Сколько молекул воздуха находится в комнате объемом V = 60 м3 при нормальных условиях? 207. В баллоне объемом V = 0,01 м3 находится газ при температуре t = 27 оС. Из-за утечки газа давление в баллоне уменьшилось на ΔР = 4,1 кПа. Сколько молекул вышло из баллона при постоянной температуре? 208. Средняя квадратичная скорость молекул газа при нормальных условиях равна vкв = 460 м/с. Сколько молекул находится в газемассы m = 1 г? 209. В баллоне объемом V = 0,20 м3 находится газ под давлением Р1 = 100 кПа и при температуре Т1 = 290 К. После накачивания газа: Р2 = 300 кПа и Т2 = 320 К. На сколько увеличилось число молекул газа в баллоне 210. Аэростат объемом V = 300 м3 наполняется водородом при температуре t = 20 оС и давлении Р = 98 кПа. Сколько времени наполняется аэростат, если в него из баллона за каждую секунду переходит водород массой m = 2,5 г/с? 211. Найти внутреннюю энергию U воздуха в комнате объемом V = 40 м3 при нормальном атмосферном давлении. Зависит ли величина U от температуры воздуха в комнате при постоянном давлении? 212. По газопроводу течет углекислый газ при давлении Р = 500 кПа и температуре t = 17 оC. Найти скорость движения газа в трубе, если за время τ = 5,0 мин через поперечное сечение трубы площадью S = 6 см2 протекает газ массой m = 2,5 кг? 213. Два теплоизолированных баллона наполнены воздухом и соединены короткой трубкой с краном. Объемы баллонов, а также давление и температура воздуха в них равны: V1, Р1, Т1 и V2, Р2, Т2. Найти температуру и давление воздуха, которые установятся после открытия крана. |
|
 , (1Ф)
, (1Ф) – постоянная Авогадро.
– постоянная Авогадро. , (2Ф)
, (2Ф) , (3Ф)
, (3Ф)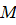 – молярная масса,
– молярная масса,  – универсальная газовая постоянная (находятся из таблицы);
– универсальная газовая постоянная (находятся из таблицы); 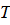 – термодинамическая температура.
– термодинамическая температура. (4Ф)
(4Ф) . (5Ф)
. (5Ф) , (6Ф)
, (6Ф) средняя кинетическая энергия поступательного движения молекулы.
средняя кинетическая энергия поступательного движения молекулы.
 . (7Ф)
. (7Ф) , (8Ф)
, (8Ф) – число степеней свободы молекулы.
– число степеней свободы молекулы.
 и постоянном давлении
и постоянном давлении 
 (10Ф)
(10Ф) и молярной
и молярной  теплоeмкостями
теплоeмкостями (11Ф)
(11Ф) (12Ф)
(12Ф)
 (14Ф)
(14Ф) сообщенной газу;
сообщенной газу;  – изменение внутренней энергии газа;
– изменение внутренней энергии газа;  : (15Ф)
: (15Ф)
 = (m/M)RΔT; (16Ф)
= (m/M)RΔT; (16Ф)
 ln(V2/V1),
ln(V2/V1), 
 = m/M – число молей газа;
= m/M – число молей газа; , или A = νR(T1 – T2)/(γ – 1), (18Ф)
, или A = νR(T1 – T2)/(γ – 1), (18Ф) (19Ф)
(19Ф) (20Ф)
(20Ф) – тепло, полученное рабочим телом от нагревателя;
– тепло, полученное рабочим телом от нагревателя;  – тепло, переданное рабочим телом холодильнику.
– тепло, переданное рабочим телом холодильнику. (21Ф)
(21Ф) и
и  – термодинамические температуры нагревателя и холодильника.
– термодинамические температуры нагревателя и холодильника. и водород массой
и водород массой  при температуре t = 10 oC и давлении Р = 1,0 МПа. Найти молярную массу смеси и объем баллона.
при температуре t = 10 oC и давлении Р = 1,0 МПа. Найти молярную массу смеси и объем баллона. (2)
(2) +
+  (3)
(3)
 и водорода
и водорода  находятся из таблицы
находятся из таблицы
 (5)
(5)

 находится гелий под давлением
находится гелий под давлением  и при температуре
и при температуре  = 27 оC. Из баллона взяли гелий массой
= 27 оC. Из баллона взяли гелий массой  , при этом темпера-тура газа понизилась до
, при этом темпера-тура газа понизилась до  = 17 оC. Найти давление
= 17 оC. Найти давление  гелия, оставшегося в баллоне.
гелия, оставшегося в баллоне. ) и конечному (
) и конечному (  ) состояниям газа, находящегося в баллоне,
) состояниям газа, находящегося в баллоне,
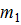 – первоначальная масса газа;
– первоначальная масса газа;  – масса газа, оставшегося в баллоне; M = 4,0.10–3кг/моль, R = 8,31 Дж/(моль.К) – молярная масса гелия и универсальная газовая постоянная (находятся из таблиц).
– масса газа, оставшегося в баллоне; M = 4,0.10–3кг/моль, R = 8,31 Дж/(моль.К) – молярная масса гелия и универсальная газовая постоянная (находятся из таблиц). находится из уравнения (2), где
находится из уравнения (2), где 

 , найденную из уравнения (1), получим ответ:
, найденную из уравнения (1), получим ответ:
 вращательного движения молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию
вращательного движения молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию  вращательного движения всех молекул кислорода массой
вращательного движения всех молекул кислорода массой  .
.





 – постоянная Авогадро (находится из таблицы);
– постоянная Авогадро (находится из таблицы);  , где
, где  – масса газа;
– масса газа;  – молярная масса кислорода (находится из таблицы), то формула (3) запишется
– молярная масса кислорода (находится из таблицы), то формула (3) запишется
 Подставляя (1) и (4) в формулу (2) и, учитывая
Подставляя (1) и (4) в формулу (2) и, учитывая  – универсальная газовая постоянная, найдем кинетическую энергию вращательного движения всех молекул кислорода:
– универсальная газовая постоянная, найдем кинетическую энергию вращательного движения всех молекул кислорода:
 и
и  находится одинаковый идеальный газ при давлениях
находится одинаковый идеальный газ при давлениях 
 и температурах
и температурах  ,
,  . Сосуды соединяют трубкой. Какая температура установится в сосудах после смешивания газов?
. Сосуды соединяют трубкой. Какая температура установится в сосудах после смешивания газов?

 ,
,  – число молей газов в первом и втором сосудах; R – универсальная газовая постоянная. Используем уравнение Менделеева – Клапейрона (3Ф) для газовв первом и втором сосудах
– число молей газов в первом и втором сосудах; R – универсальная газовая постоянная. Используем уравнение Менделеева – Клапейрона (3Ф) для газовв первом и втором сосудах



 или учитывая (3), получим:
или учитывая (3), получим:
 , или, учитывая
, или, учитывая  , получим:
, получим:
 и
и 
 (закон сохранения энергии), откуда с учетом (4) и (6), найдем искомую температуру
(закон сохранения энергии), откуда с учетом (4) и (6), найдем искомую температуру
 находится при температуре
находится при температуре  и рас-ширяется при постоянном давлении, при этом объем увеличивается в n = 2,0 раза. Найти
и рас-ширяется при постоянном давлении, при этом объем увеличивается в n = 2,0 раза. Найти

 – молярная масса кислорода;
– молярная масса кислорода;  – универсальная газовая постоянная;
– универсальная газовая постоянная;  – приращение температуры. Работа газа при изобарном процессе (16Ф)
– приращение температуры. Работа газа при изобарном процессе (16Ф) (3)
(3) , (4)
, (4) , откуда с учетом условия задачи
, откуда с учетом условия задачи



 , охладили изохорно, вследствие чего его давление уменьшилось в n = 2,0 раза. Затем газ изобарно расширили так, что в конечном состоянии его температура стала равной первоначальной. Найти количество теплоты, поглощенной газом в данном процессе.
, охладили изохорно, вследствие чего его давление уменьшилось в n = 2,0 раза. Затем газ изобарно расширили так, что в конечном состоянии его температура стала равной первоначальной. Найти количество теплоты, поглощенной газом в данном процессе. ,
,  – диаграмме (см. рис. 20). Количество теплоты находится из перво- ν = 2. го начала термодинамики
– диаграмме (см. рис. 20). Количество теплоты находится из перво- ν = 2. го начала термодинамики = 0. Следовательно, в данном процессе работа А = А23 = P2 ΔV. Применяя уравнение Менделеева – Клапейрона (3Ф) к состояни-
= 0. Следовательно, в данном процессе работа А = А23 = P2 ΔV. Применяя уравнение Менделеева – Клапейрона (3Ф) к состояни-



 Тогда из (1) искомое количество теплоты
Тогда из (1) искомое количество теплоты  . Учитывая (3), получим:
. Учитывая (3), получим:
 = 1) идеального газа с числом степеней свободы молекул
= 1) идеального газа с числом степеней свободы молекул  – постоянная. Найти количество теплоты, полученной газом в этом процессе, если его температура испытала приращение
– постоянная. Найти количество теплоты, полученной газом в этом процессе, если его температура испытала приращение  .
. , (2)
, (2)
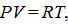




 массой m = 20,0 г находится при температуре
массой m = 20,0 г находится при температуре 











 (см. рис. 21). Параметры газа можно определить из уравнений адиабатического и изотермического процессов. При адиабатическом процессе температура и объем идеального газа в состояниях 1 и 2 связаны между собой уравнением Пуассона (19Ф)
(см. рис. 21). Параметры газа можно определить из уравнений адиабатического и изотермического процессов. При адиабатическом процессе температура и объем идеального газа в состояниях 1 и 2 связаны между собой уравнением Пуассона (19Ф)

 . Для молекулярного водорода (число степеней сво-боды
. Для молекулярного водорода (число степеней сво-боды  = 5) молярная теплоемкость при постоянном давлении
= 5) молярная теплоемкость при постоянном давлении  . (R – универсальная газовая постоянная). Молярная теплоемкость при постоянном объеме
. (R – универсальная газовая постоянная). Молярная теплоемкость при постоянном объеме  , тогда γ = 1,4. Подставляя это значение γ в (1), найдем температуру:
, тогда γ = 1,4. Подставляя это значение γ в (1), найдем температуру: 
 (находится из таблицы). Работа газа при изотермическом процессе (17Ф)
(находится из таблицы). Работа газа при изотермическом процессе (17Ф)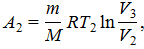
 =
= 
 . Знак «минус» показывает, что при сжатии газа работа совершается внешними силами. Для определения приращения внутренней энергии газа при адиабатическом процессе воспользуемся первым началом термодинамики (14Ф)
. Знак «минус» показывает, что при сжатии газа работа совершается внешними силами. Для определения приращения внутренней энергии газа при адиабатическом процессе воспользуемся первым началом термодинамики (14Ф)
 = 0 и
= 0 и  =
=  . С учетом (2) имеем
. С учетом (2) имеем

 за цикл затрачивается внешними силами на изотермическое сжатие рабочего тела?
за цикл затрачивается внешними силами на изотермическое сжатие рабочего тела?

 .
.


 , переданное рабочему телу от нагревателя:
, переданное рабочему телу от нагревателя:  , откуда с учетом (2)
, откуда с учетом (2)



 . Используя (4), найдем:
. Используя (4), найдем:




 где
где  – температура нагревателя и холодильника. Используем для адиабатического процесса уравнение Пуассона (19Ф) в виде
– температура нагревателя и холодильника. Используем для адиабатического процесса уравнение Пуассона (19Ф) в виде


 = 1,4 – постоянная адиабаты для двухатомного водорода. По условию задачи
= 1,4 – постоянная адиабаты для двухатомного водорода. По условию задачи  . Тогда из (2)
. Тогда из (2)


 ,
,


 = 4.0 раза. Найти приращение энтропии.
= 4.0 раза. Найти приращение энтропии. He,
He, 




 , или в интегральной форме для равновесных (квазистатических) процессов
, или в интегральной форме для равновесных (квазистатических) процессов

 – элементарное количество теплоты, находится из первого начала термодинамики (14Ф), записанного в дифференциальной форме,
– элементарное количество теплоты, находится из первого начала термодинамики (14Ф), записанного в дифференциальной форме,

 – универсальная газовая постоянная (находится из таблицы).
– универсальная газовая постоянная (находится из таблицы).
 , с учетом того, что процесс изобарный:
, с учетом того, что процесс изобарный:  . Тогда (4) запишется
. Тогда (4) запишется


 – число степеней свободы атомов гелия. Для изобарного процесса T1/V1 = T2/V2, откуда с учетом условия задачи имеем:
– число степеней свободы атомов гелия. Для изобарного процесса T1/V1 = T2/V2, откуда с учетом условия задачи имеем:
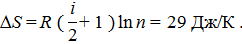
 = 300 К и сжимается от объема V1 до объема V2 = V1/2 один раз изотермически, а другой раз – адиабатически. Найти приращение энтропии и конечную температуру
= 300 К и сжимается от объема V1 до объема V2 = V1/2 один раз изотермически, а другой раз – адиабатически. Найти приращение энтропии и конечную температуру 




 (1)
(1) находится из первого начала термодинамики (14Ф) в дифференциальной форме
находится из первого начала термодинамики (14Ф) в дифференциальной форме . (4)
. (4) .
. .
. 2 = – 5,76 Дж/К.
2 = – 5,76 Дж/К. , тогда из (1) видно, что
, тогда из (1) видно, что  , т. е. энтропия или при данном процессе остается постоянной.
, т. е. энтропия или при данном процессе остается постоянной. откуда
откуда
