|
|
Принцип действия ускорителя заряженных частиц.Рассмотрим в качестве примера ускорителя циклотрон. Циклотрон состоит из двух электродов в виде половинок круговой коробки, которые называются дуантами. На дуанты подается переменное напряжение. Поскольку дуанты металлические, пространство внутри дуантов эквипотенциальное, внутри только магнитное поле электромагнитов, между полюсами которых и помещены дуанты (поле перпендикулярно к дуантам).
К моменту, когда частица влетит в зазор между дуантами, напряжение снова изменит знак и примет амплитудное значение. Частица движется по кривой, близкой к спирали, получая при каждом прохождении через зазор дополнительную порцию энергии. На последнем витке пучок быстрых заряженных частиц выводится наружу, бомбардируя частицы мишени.
10. Опыт Фарадея (англ. ученый 1791-1867).
Магнитный поток (поток магнитной индукции). Магнитный поток ЭДС индукции. Вывод основного закона электромагнитной индукции. Найдем связь между ЭДС индукции
Действие этой силы эквивалентно действию на электрон электрического поля напряженностью:
По определению ЭДС (
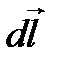 и нормаль к контуру образовывали правовинтовую систему. Вынесем за знак интеграла и нормаль к контуру образовывали правовинтовую систему. Вынесем за знак интеграла 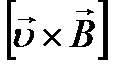 (интегрирование ведется по длине перемычки) и проведем интегрирование: (интегрирование ведется по длине перемычки) и проведем интегрирование:
ЭДС индукции в контуре равна скорости изменения магнитного потока, пронизывающего этот контур, взятой с обратным знаком. Правило Ленца. Индукционный ток всегда направлен ток, чтобы противодействовать изменению магнитного потока, вызвавшего этот ток. Так как перемычка двигается так, что площадь контура, ограниченного проводником и перемычкой, увеличивается, соответственно магнитный поток увеличивается, то индукционное поле 11. Энергия магнитного поля.
Подставляя значение индуктивности соленоида
Учитывая все, получим:
Физика 4 раздел. Колебания и волны 1. Колебания – движение или процессы, обладающие той или иной степенью повторности во времени. Гармонические (или синусоидальные) колебания – разновидность периодических колебаний, которые могут быть заменены в виде
где a – амплитуда, Амплитуда (а) – наибольшее отклонение от среднего значения величины, совершающей колебания. Фаза колебаний ( ) Фаза характеризует значение изменяющейся величины в данный момент времени. Значение
Свободные колебания. Свободными или собственными называются такие колебания, которые происходят в системе, выведенной из положения равновесия и предоставленной самой себе.
(линейное – т.е. и сама величина х, и ее производная в первой степени; однородное – т.к. нет свободного члена, не содержащего х ; второго порядка – т.к. вторая производная х). Если величины, описывающие колебания некоторой системы периодически изменяются со временем, то для такой системы пользуются термином «осциллятор». Линейным гармоническим осциллятором называется такой, движение которого описывается линейным уравнением 2.
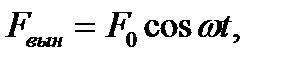 где где  - частота вынуждающей силы. Уравнение движения запишется с учетом всех сил ( - частота вынуждающей силы. Уравнение движения запишется с учетом всех сил ( 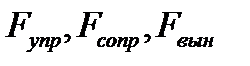 ) запишется в виде ) запишется в виде
Уравнение является неоднородным. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения
(14)
Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных Механический резонанс. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

резонансная частота
 →0 все кривые приходят к одному и тому же значению →0 все кривые приходят к одному и тому же значению  , , 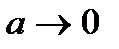 . При . При 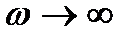 , ,  . Чем меньше . Чем меньше 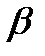 , тем острее максимум. , тем острее максимум.
3. Механизм образования механических волн в упругой среде. Если в каком-либо месте упругой среды (твердой, жидкой или газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью. Процесс распространения колебаний в пространстве называется волной. Геометрическое место точек, до которых доходят колебания к моменту времени t называется фронтом волны (волновым фронтом). В зависимости от формы фронта волна может быть сферической, плоской и др. Волна называется продольной, если направление смещения частиц среды совпадает с направлением распространения волны.Продольная волна распространяется в твердых, жидких и газообразных средах. Волна называется поперечной, если смещение частиц среды перпендикулярно направлению распространения волны. Поперечная механическая волна распространяется только в твердых телах (в средах обладающих сопротивлением сдвигу, поэтому в жидкостях и газах такая волна распространиться не может). |
|
 , но т.к. период постоянен, время, за которое частица пройдет половину окружности, остается прежним.
, но т.к. период постоянен, время, за которое частица пройдет половину окружности, остается прежним.

 вектора магнитной индукции через элементарную площадку
вектора магнитной индукции через элементарную площадку  (рис.25.2) определяется скалярным произведением векторов
(рис.25.2) определяется скалярным произведением векторов 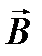 и
и  . Единица измерения магнитного потока в системе СИ
. Единица измерения магнитного потока в системе СИ 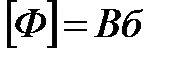 .
.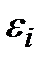 и скоростью изменения магнитного потока.
и скоростью изменения магнитного потока.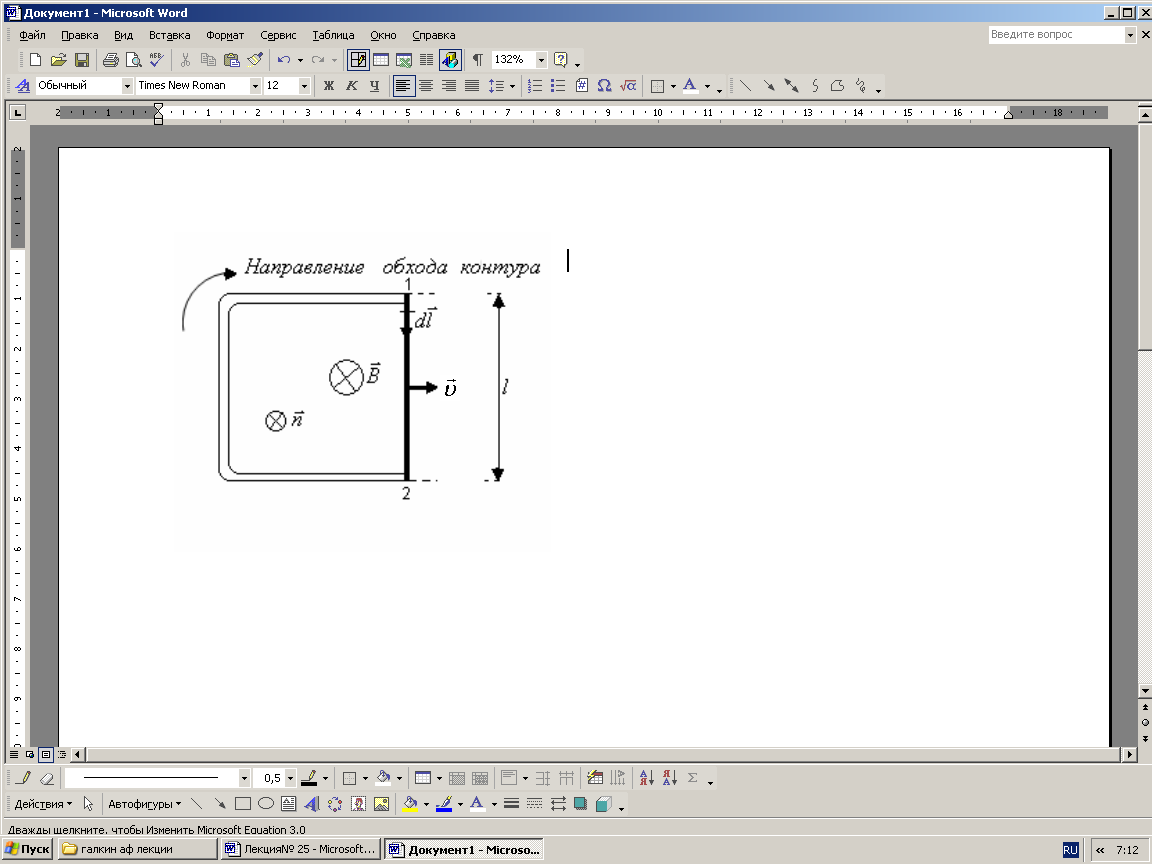
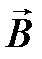 . Приведем перемычку в движение со скоростью
. Приведем перемычку в движение со скоростью  . С той же скоростью станут перемещаться относительно поля и носители тока в перемычке – электроны. На каждый электрон начнет действовать направленная вдоль перемычки магнитная сила (магнитная составляющая силы Лоренца).
. С той же скоростью станут перемещаться относительно поля и носители тока в перемычке – электроны. На каждый электрон начнет действовать направленная вдоль перемычки магнитная сила (магнитная составляющая силы Лоренца).
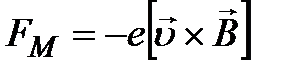 (заряд электрона
(заряд электрона  ).
).
 .
.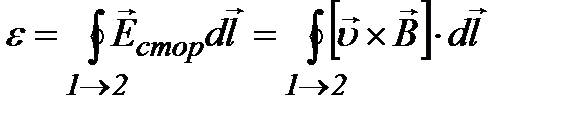 ,
, лишь на участке 1-2).
лишь на участке 1-2).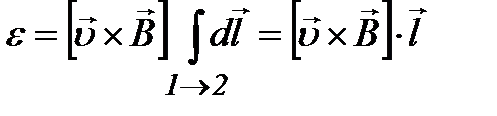 ,
,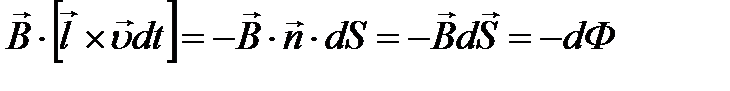 .
.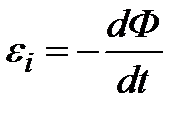
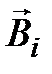 направлено для ослабления изменения магнитного потока в сторону, противоположную направлению внешнего поля
направлено для ослабления изменения магнитного потока в сторону, противоположную направлению внешнего поля  . Индукционный ток
. Индукционный ток 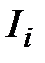 в соответствии с правилом буравчика направлен против хода часовой стрелки.
в соответствии с правилом буравчика направлен против хода часовой стрелки.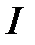 , который обусловит магнитное поле, сцепленное с витками соленоида. Если разомкнуть ключ, то через сопротивление
, который обусловит магнитное поле, сцепленное с витками соленоида. Если разомкнуть ключ, то через сопротивление 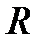 будет течь постепенно убывающий ток, поддерживаемый возникающей в соленоиде ЭДС самоиндукции. Работа, совершаемая этим током за счет энергии магнитного поля за время
будет течь постепенно убывающий ток, поддерживаемый возникающей в соленоиде ЭДС самоиндукции. Работа, совершаемая этим током за счет энергии магнитного поля за время  :
:

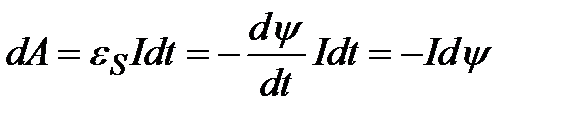 ,
,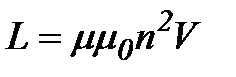 и учитывая, что
и учитывая, что 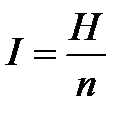 :
: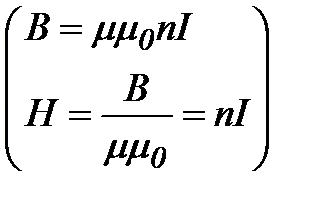 .
. . Поскольку работа совершается за счет энергии магнитного поля катушки, то
. Поскольку работа совершается за счет энергии магнитного поля катушки, то 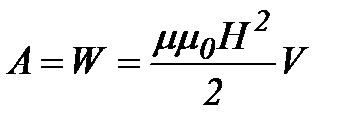 , отсюда объемная плотность энергии магнитного поля:
, отсюда объемная плотность энергии магнитного поля:
 (1)
(1) - фаза,
- фаза,  - начальная фаза,
- начальная фаза, 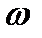 - циклическая частота, t – время (т.е. применяются со временем по закону синуса или косинуса).
- циклическая частота, t – время (т.е. применяются со временем по закону синуса или косинуса).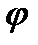 – изменяющийся аргумент функции, описывающей колебательный процесс (величина
– изменяющийся аргумент функции, описывающей колебательный процесс (величина  t+
t+ 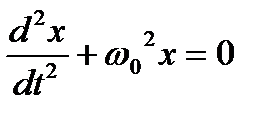
 .
.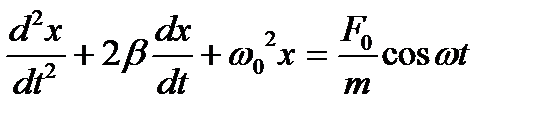

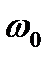 и
и  ) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания также зависит от частоты вынуждающей силы.
) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания также зависит от частоты вынуждающей силы.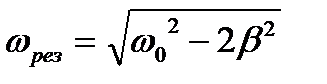



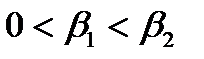
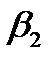

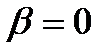
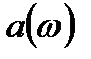
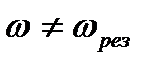 , то между вынуждающей силой
, то между вынуждающей силой 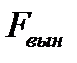 и скоростью
и скоростью 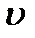 существует определенная разность фаз, поэтому в течение некоторой доли каждого периода сила
существует определенная разность фаз, поэтому в течение некоторой доли каждого периода сила