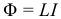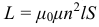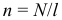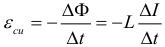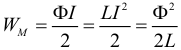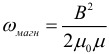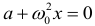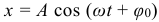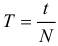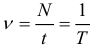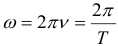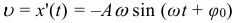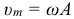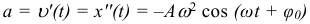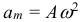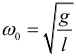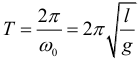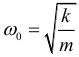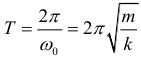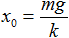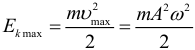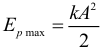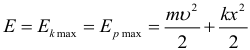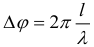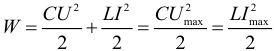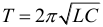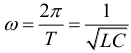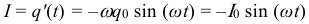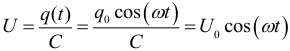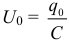Индуктивность. Самоиндукция. Энергия магнитного поля

К оглавлению...

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции илииндуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).

Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:

где: n - концентрация витков на единицу длины катушки:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:

Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. ЭнергияW_м магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):

Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):

Правило Ленца

К оглавлению...

Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.

Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.

Основные теоретические сведения

Гармонические колебания

К оглавлению...

В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными.Колебаниями называют изменения физической величины, происходящие по определенному закону во времени. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Для существования в системе гармонических колебаний необходимо, чтобы у нее было положение устойчивого равновесия, то есть такое положение, при выведении из которого на систему начала бы действовать возвращающая сила.

Механические колебания, как и колебательные процессы любой другой физической природы, могут бытьсвободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.

Простейшим видом колебательного процесса являются колебания, происходящие по закону синуса или косинуса, называемые гармоническими колебаниями. Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω₀ задаётся следующим образом:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний, которое имеет вид:

где: x – смещение тела от положение равновесия, A – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2Π/T), t – время. Величина, стоящая под знаком косинуса: φ = ωt + φ₀, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t = 0 получаем, что φ = φ₀, поэтому φ₀называют начальной фазой (то есть той стадией, из которой начиналось колебание).

Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Если же количество колебаний N, а их время t, то период находится как:

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Максимальные по модулю значения скорости υ_m = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях. Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Знак минус в предыдущем выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, возвращает тело в начальное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.

Следует обратить внимание на то, что:

· физические свойства колебательной системы определяют только собственную частоту колебаний ω₀ или период T.

· Такие параметры процесса колебаний, как амплитуда A = x_m и начальная фаза φ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени, т.е. начальными условиями.

· При колебательном движении тело за время, равное периоду, проходит путь, равный 4 амплитудам. При этом тело возвращается в исходную точку, то есть перемещение тела будет равно нулю. Следовательно, путь равный амплитуде тело пройдет за время равное четверти периода.

Чтобы определить, когда в уравнение колебаний подставлять синус, а когда косинус, нужно обратить внимание на следующие факторы:

· Проще всего, если в условии задачи колебания названы синусоидальными или косинусоидальными.

· Если сказано, что тело толкнули из положения равновесия – берем синус с начальной фазой, равной нулю.

· Если сказано, что тело отклонили и отпустили – косинус с начальной фазой, равной нулю.

· Если тело толкнули из отклоненного от положения равновесия состояния, то начальная фаза не равна нолю, а брать можно и синус и косинус.

Математический маятник

К оглавлению...

Математическим маятником называют тело небольших размеров, подвешенное на тонкой, длинной и нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Только в случае малых колебаний математический маятник является гармоническим осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Полученная формула называется формулой Гюйгенса и выполняется, когда точка подвеса маятника неподвижна. Важно запомнить, что период малых колебаний математического маятника не зависит от амплитуды колебаний. Такое свойство маятника называется изохронностью. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника выполняются следующие соотношения:

1. Путь от положения равновесия до крайней точки (или обратно) проходится за четверть периода.

2. Путь от крайней точки до половины амплитуды (или обратно) проходится за одну шестую периода.

3. Путь от положения равновесия до половины амплитуды (или обратно) проходится за одну двенадцатую долю периода.

Пружинный маятник

К оглавлению...

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению. Таким свойством обладает сила упругости.

Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную совершать в отсутствие трения свободные гармонические колебания. Груз на пружине называют пружинным маятником.

Циклическая частота колебаний пружинного маятника рассчитывается по формуле:

Период колебаний пружинного маятника:

При малых амплитудах период колебаний пружинного маятника не зависит от амплитуды (как и у математического маятника). При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x₀, равную:

А колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω₀ и периода колебаний T справедливы и в этом случае. Таким образом, полученная формула для периода колебаний груза на пружине остается справедливой во всех случаях, независимо от направления колебаний, движения опоры, действия внешних постоянных сил.

При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника – это энергия в поле тяготения Земли.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией (как правило, потенциальную энергию в положении равновесия полагают равной нулю). Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и так далее.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. При этом, максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса (полная механическая энергия равна максимальным значениям кинетической и потенциальной энергий, а также сумме кинетической и потенциальной энергий в произвольный момент времени):

Механические волны

К оглавлению...

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называетсяпоперечной. Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют немеханические волны, которые способны распространяться и в пустоте (например, световые, т.е. электромагнитные волны могут распространяться в вакууме).

· Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.

· Поперечные волны не могут существовать в жидкой или газообразной средах.

Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой ν и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.

Длиной волны λ называют расстояние между двумя соседними точками, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за время равное периоду T, следовательно, длина волны может быть рассчитана по формуле:

где: υ – скорость распространения волны. При переходе волны из одной среды в другую длина волны и скорость ее распространения меняются. Неизменными остаются только частота и период волны.

Разность фаз колебаний двух точек волны, расстояние между которыми l рассчитывается по формуле:

Электрический контур

К оглавлению...

В электрических цепях, так же, как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный LC-контур. В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими. Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в теплоту, выделяющуюся на резисторе, и колебания становятся затухающими.