|
|
Числовые характеристики распределенияВведение Закономерности в экономике выражаются в виде зависимостей экономических показателей и математических моделей их поведения. Такие зависимости и модели могут быть получены только путем обработки реальных статистических данных, с учетом внутренних механизмов связи и случайных факторов. Термин «эконометрика» был введен в 1926 г. .норвежским ученым Р. Фришем и в дословном переводе означает «эконометрические измерения». Наряду с таким широким пониманием эконометрики, порождаемым переводом самого термина, встречается и весьма узкая трактовка эконометрики как набора математико-статистических методов, используемых в приложениях математики в экономике. Эконометрика – наука, изучающая количественные закономерности и взаимозависимости в экономике методами математической статистики. Цель эконометрики – эмпирический вывод экономических законов. Задачи эконометрики– построение экономических моделей и оценивание их параметров, проверка гипотез о свойствах экономических показателей и формах их связи. Таким образом, эконометрика есть единство трех составляющих – статистики, экономической теории и математики. Эконометрический анализ служит основой для экономического анализа и прогнозирования, создавая возможность для принятия обоснованных экономических решений. Широкому внедрению эконометрических методов способствовало появление во второй половине XX в. электронных вычислительных машин. Компьютерные эконометрические пакеты сделали эти методы более доступными и наглядными, так как наиболее трудоемкую работу по расчету различных статистик, параметров, характеристик, построению таблиц и графиков в основном стал выполнять компьютер, а эконометристу осталась главным образом творческая работа: постановка задачи, выбор соответствующей модели и метода ее решения, интерпретация результатов. Типы данных При моделировании экономических процессов встречаются с двумя типами данных: пространственными и временными. Пространственные данные –это данные по какому-либо экономическому показателю, полученные от разных однотипных объектов (фирм, регионов и т.п.), но относящиеся к одному и тому же моменту времени (пространственный срез). Например, данные об объеме производства, количестве работников, доходе разных фирм в один и тот же момент времени. Временные ряды – это данные, характеризующие один и тот же объект в различные моменты времени (временной срез). Например, ежеквартальные данные об инфляции, средней заработанной плате, данные о национальном доходе за последние годы. Отличительная черта временных данных – упорядоченность во времени. Кроме того, наблюдения в близкие моменты времени часто бывают зависимы. Любые экономические данные представляют характеристики какого-либо экономического объекта. Они формируются под воздействием множества факторов, не все из которых доступны внешнему контролю. Неконтролируемые (неучтенные) факторы обусловливают случайность данных, которые они определяют. Поскольку экономические данные имеют статистическую природу, для их анализа и обработки необходимо применять специальные методы.
Классы моделей Можно выделить три основных класса моделей: модели временных рядов, регрессионные модели с одним уравнением и системы одновременных уравнений. 1. Модели временных рядов.К этому классу относятся модели тренда и сезонности. Тренд представляет собой устойчивое изменение уровня показателя в течение длительного времени. Сезонность характеризует устойчивые внутригодовые колебания уровня показателя. К моделям временных рядов относятся множество более сложных моделей, например, модель адаптивного прогноза, модель авторегрессии. Их общей чертой является то, что они объясняют поведение временного ряда, исходя только из его предыдущих значений. 2. Регрессионные модели с одним уравнением.В таких моделях объясняемая переменная представляется в виде функции от объясняющих переменных. Например, модель спроса на некоторый товар в зависимости от его цены и дохода. По виду функции регрессионные модели делятся на линейные и нелинейные. Существуют эффективные методы оценки и анализа линейных регрессионных моделей. Анализ линейных регрессионных моделей является базовым в прикладной эконометрике. Область применения регрессионных моделей значительно шире, чем моделей временных рядов. 3. Системы одновременных уравнений.Эти модели описываются системами уравнений, состоящими из тождеств и регрессионных уравнений, в каждом из которых аргументы помимо объясняющих переменных содержат объясняемые переменные из других уравнений системы. Например, модель формирования доходов. Все три класса моделей могут использоваться при моделировании экономических процессов. Обычно предполагают, что все факторы, не учтенные явно в экономической модели, оказывают на объект некоторое результирующее воздействие, величина которого задается случайной компонентой. Введение случайной компоненты в экономическую модель делает её доступной для эмпирической проверки на основе статистических данных. Типы зависимостей В экономических исследованиях одной из основных задач является анализ зависимостей между переменными. Зависимость может быть функциональной либо статистической. Функциональная зависимость задается в виде точной формулы, каждому значению одной переменной соответствует строго определенное значение другой, воздействием случайных факторов при этом пренебрегают. В экономике функциональная зависимость между переменными проявляется редко. Статистической зависимостью называется связь переменных, на которую накладывается воздействие случайных факторов. При этом изменение одной переменной приводит к изменению математического ожидания другой переменной. Уравнение регрессии – это формула статистической связи между переменными. Если эта формула линейна, то имеем линейную регрессию. Формула статистической связи двухпеременных называется парной регрессией, зависимость от нескольких переменных – множественной регрессией. Глава 1. Элементы математической статистики Операция суммирования Пусть величина X задается последовательность данных x1, x2,…, xn, каждое из которых можно записать как xi, i = 1, …, n. Сумма этих чисел обозначается:
Если из контекста ясно, каковы начальный и конечный суммируемые члены, то часто используют сокращенные обозначения:
Сумма квадратов этих чисел обозначается:
Обозначим средние значения величин X, X2, XY соответственно как:
Имеет место неравенство: Правила суммирования (a, b – константы): 1. 2. 3. 4. 5. 6. 7. Случайные величины Случайной величиной (переменной) называется величина, которая под воздействием случайных факторов может с определенными вероятностями принимать те или иные значения из некоторого множества чисел. Случайные величины обозначаются прописными буквами, а их возможные значения – строчными. Для полной характеристики случайной величины должны быть указаны не только все ее значения, но и их вероятности. Универсальным способом задания случайной величины Х является задание её функции распределения. Функцией распределения F(x) случайной величины X называется вероятность того, что величина X принимает значение, меньшее x, т.е.
Свойства функции распределения: 1)0 ≤ F(x) ≤ 1 при любых x Î R; 2) P(x1 3) F(x) – неубывающая функция; 4) Различают дискретные и непрерывные случайные величины. Дискретной называется случайная величина, которая принимает отдельные, изолированные друг от друга значения. Число возможных значений дискретной случайной величины конечно или счётно. Дискретную случайную величину удобнее задавать не в виде функции распределения, а рядом распределения. При табличном задании ряда распределения первая строка таблицы содержит возможные значения случайной величины, а вторая – соответствующие им вероятности, т.е.
Графическое изображение ряда распределения называется полигоном распределения. Непрерывнойназывается случайная величина, множество значений которой непрерывно заполняет некоторый числовой промежуток. Число возможных значений непрерывной случайной величины бесконечно. Задать непрерывную случайную величину рядом распределения невозможно, поэтому её задают функцией распределения F(x). Вместо функции распределения F(x) для непрерывной случайной величины обычно используется плотность распределения вероятностей f(x). Плотностью распределения f(x) непрерывной случайной величины называется производная от функции распределения, т.е. f(x) = F¢(x). Свойства плотности распределения: 1) f(x) 2) 3)
В основе математической статистики лежат понятия генеральной и выборочной совокупностей. Генеральная совокупность – множество всех значений (исходов) случайной величины, которые она может принять в процессе наблюдения. Например, данные о доходах всех жителей страны. Выборочная совокупность (выборка) – множество наблюдений, составляющих лишь часть генеральной совокупности. Для любой случайной величины важную роль, помимо функции распределения, играют числовые характеристики её распределения.
Числовые характеристики распределения Генеральная совокупность Математическим ожиданием дискретной случайной величины называется сумма произведений всех её значений на соответствующие им вероятности, т.е.
где суммирование производится по всем возможным значениям случайной величины. Математическое ожидание непрерывной случайной величины определяется выражением:
где интегрирование производится на всем интервале, в котором определена функция f(x). Математическое ожидание случайной величины – это среднее ее значение по генеральной совокупности, обозначается Геометрически математическое ожидание случайной величины – это центрее распределения. Математическое ожидание функции g(X) определяется выражением:
где суммирование производится по всем возможным значениям xi. В частности, если g(X) = X2, то M(X2) = Sxi2 pi. Теоретическая (генеральная) дисперсия случайной величины определяется как математическое ожидание квадрата отклонения случайной величины X относительно её средней, т.е.
Замечание. Если ясно, о какой переменной идет речь, нижний индекс в Для вычисления дисперсии часто используется другое выражение, получаемое из определения дисперсии:
Геометрически дисперсия – мера рассеяния случайной величины относительно средней (центра). Размерность дисперсии не совпадает с размерностью случайной величины. Стандартным отклонением случайной величины X называется корень квадратный из её дисперсии, т.е. Стандартное отклонение показывает, насколько в среднем отклоняется случайная величина в совокупности относительно средней (центра). Определение. Случайные величины X, Y называются независимыми, если P(X = x; Y = y)= P(X = x) P(Y = y) для любых значений x, y. Следствие.Если случайные величины X,Y независимы, то M(XY) = M(X)M(Y),
Заметим, что M(X) и D(X) – это числовые характеристики генеральной совокупности (числа), а не функции. Нормальное распределение случайной величины X характеризуется лишь двумя параметрами: средним значением m и дисперсией s2. Это обозначается как X ~ N(m, s2). График плотности нормального распределения f(x) имеет колоколообразный вид (рис. 1), симметричный относительно центра m. Максимум этой функции находится в точке x = m, а разброс относительно этой точки определяется параметром s. Чем меньше значение s, тем более острый и высокий максимум f(x).
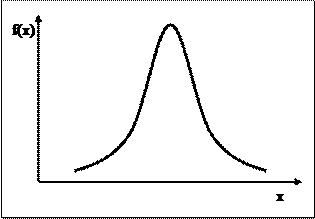
Рис. 1 II. Выборочная совокупность Пусть из генеральной совокупности с распределением F(x) извлекается выборка объема n. Считаем, что выборочные наблюдения X1, X2,…, Xn независимы и имеют одинаковые распределения. Выборочной средней называется среднее арифметическое наблюдаемых значений случайной величины в выборке, т.е.
Выборочной дисперсией (вариацией) называется среднее арифметическое квадратов отклонения наблюдаемых значений случайной величины в выборке от их среднего значения, т.е.
Свойства выборочной дисперсии, (a, b – const):
Значения Для разных выборок, взятых из одной и той же генеральной совокупности, выборочные средние и дисперсии будут различны, т.е. выборочные характеристики являются случайными величинами. Замечание. Математическое ожидание М(Х) – это операция нахождения средней из выборочных средних гипотетических выборок, покрывающих генеральную совокупность. Из условия, что выборочные наблюдения X1, X2, …, Xn независимы и имеют одинаковые распределения, вытекает, что:
Центральная предельная теорема закона больших чисел устанавливает, что распределение средней выборочной
Пример. 1.1.Вычислить выборочные характеристикипо исходным данным
Исходные данные (x) и расчетные показатели (
Выборочные характеристики:
Для вычисления выборочных средней и дисперсии в Excel можно использовать функции: |
|
 , причем
, причем 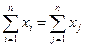 .
. .
.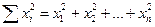
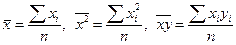
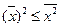 .
.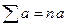
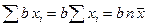
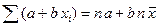
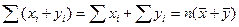


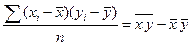
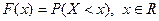 .
.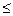 X
X  .
.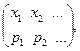 гдеpi = P(X = xi), Spi = 1.
гдеpi = P(X = xi), Spi = 1.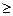 0 при любых x Î R
0 при любых x Î R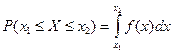
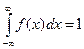
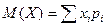 ,
,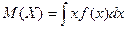 ,
,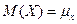 .
.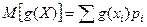 ,
, .
. или
или 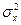 может быть опущен.
может быть опущен.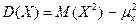 .
.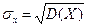 .
.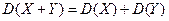 .
.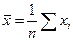 .
.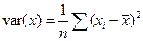 , или
, или  .
.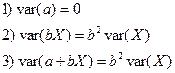
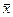 ,var(X) являются числовыми характеристиками выборочной совокупности.
,var(X) являются числовыми характеристиками выборочной совокупности. .
.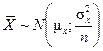 .
.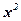 ) представим в виде расчетной таблицы.
) представим в виде расчетной таблицы.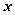
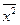
 132 – 100 =32.
132 – 100 =32.