|
|
Точечные и интервальные оценкиХарактеристики генеральной совокупности обычно неизвестны. Задача заключается в их оценке по характеристикам выборочной совокупности. Характеристики генеральной совокупности принято называть параметрами, а выборочной совокупности – оценками. Пусть искомый параметр генеральной совокупности есть q0, а на основе выборки объема n определяется оценка q. Различают точечные и интервальные оценки параметров генеральной совокупности. Точечной оценкой q параметра q0 называется числовое значение этого параметра, полученное по выборке, т.е. q0 ≈ q. Для того, чтобы выборочная оценка давала хорошее приближение оцениваемого параметра, она должна удовлетворять определенным требованиям (несмещенности, эффективности и состоятельности). 1. Несмещенность оценок. Оценка q является несмещенной, если её математическое ожидание равно оцениваемому параметру q0 при любом объеме выборки, т.е. M(q) = q0. Если это не так, то оценка называется смещенной, а разность M(q) – q0 –смещением. Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании. Выборочная средняя Выборочная дисперсия var(x) является смещенной оценкой генеральной дисперсии
В качестве несмещенной оценки генеральной дисперсии используется величина (исправленная дисперсия):
Отметим, что в знаменателе остаточной дисперсии стоит число степеней свободы (n – 1), а не n, так как одна степень свободы теряется при определении выборочной средней. Замечание. Для получения несмещенной оценки дисперсии случайной величины соответствующую сумму квадратов отклонений от средней делят на число степеней свободы, т.е. на число свободы независимого варьирования случайной величины. Число степеней свободы равно разности между числом единиц совокупности n и числом определяемых по ней констант. Стандартным отклонением sx случайной величины в выборке называется корень квадратный из ее исправленной дисперсии:
По данным примера 1 определим
Для вычисления исправленной дисперсии и стандартного отклонения в Excel используют функции: sx2=DИСП(массив x), sx = СТАНДОТКЛОН(массив x). 2. Эффективность оценок. Несмещенная оценка q называется эффективной, если она имеет минимальную дисперсию по сравнению с другими выборочными оценками, т.е. minD(q). Предположим, что имеются две оценки параметра q0, рассчитанные на основе одной и той же информации (рис. 2). Оценка A является более эффективной, чем оценка B, т.к. имеет меньшую дисперсию.
Рис. 2.
Выборочная средняя 3. Состоятельность оценок. Оценка q называется состоятельной, если при
Иначе говоря,состоятельной называется такая оценка, которая дает точное значение для большой выборки независимо от входящих в нее конкретных наблюдений. На рис. 3 показано, как при различном объеме выборки может выглядеть распределение вероятностей (состоятельная оценка, смещенная на малой выборке).
Рис. 3
Теорема Чебышева закона больших чисел утверждает, что
т.е. выборочная средняя Пусть выборочная характеристика q служит оценкой неизвестного параметра q0. Наряду с точечными оценками параметров (в виде одного числа) рассматривают интервальные оценки (в виде двух чисел – концов интервала). Интервальной называют оценку, определяющую числовой интервал (q – e; q + e ), e >0, содержащий оцениваемый параметр q0, т.е. q – e < q0< q + e, или |q – q0|< e Доверительным интервалом называется интервал |q – q0| < e, в котором с заданной вероятностью g заключен неизвестный параметр q0, а сама вероятность называется доверительной вероятностью, т.е. P(|q – q0 | < e ) = g Уровнем значимости a называется вероятность P(|q – q0 | > e ) = a, причем a = 1 – g.
|
|
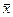 является несмещеннойоценкой генеральной средней m, т.к. M(
является несмещеннойоценкой генеральной средней m, т.к. M( 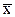 не единственная возможная несмещенная оценка m.
не единственная возможная несмещенная оценка m.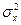 , при этом:
, при этом: .
. для которой
для которой  .
.
 , s2:
, s2: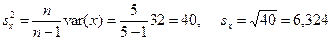

 она стремится по вероятности к оцениваемому параметру q0, т.е.
она стремится по вероятности к оцениваемому параметру q0, т.е.

