|
|
Абсорбция (поглощение) света коллоидами и окраска коллоидных растворовОкраска коллоидных растворов, как и других дисперсных систем, связана с явлениями рассеяния и поглощения света. Поглощение света имеет четко выраженный избирательный характер. Рассеяние света придает коллоиду красноватую окраску в проходящем свете и голубоватую – в рассеянном. В целом окраска коллоидных растворов определяется наложением двух эффектов – рассеяния и поглощения света. С изменением дисперсности или формы частиц дисперсной фазы изменяется вклад обоих эффектов, что вызывает изменения окраски дисперсной системы. Для молекулярных растворов поглощение света можно количественно описать формулой Ламберта-Бера:
где I и I0 – интенсивность падающего света и света, прошедшего через раствор; с – концентрация растворенного вещества; d- толщина слоя раствора; k – коэффициент поглощения. Относительная прозрачность может быть выражена отношением
относительное поглощение –
Для коллоидных растворов в формулу (1.5) должна быть внесена поправка, учитывающая рассеяние света, которое эквивалентно дополнительному поглощению света. Одна из модификаций формулы (1.5), учитывающая светорассеяние, имеет вид:
где V – объем коллоидной частицы. Для золей металлов все закономерности намного сложнее. Для них отмечается аномалия как в поглощении света, так и в рассеянии. При этом для них характерно значительное поглощение света, что определяет интенсивность их окраски. Для обоих оптических эффектов наблюдаются максимумы, зависящие от длины волны и степени дисперсности золя. Так, соли золота с частицами близкими к сферической форме радиусом 20 нм имеют максимум адсорбции при l=530 нм, что отвечает адсорбции зеленых лучей. Соответственно они приобретают красную окраску. Соли золота с радиусом 30 нм имеют максимум адсорбции при l=600 нм. При этом золь приобретает синюю окраску. Приведенные данные находятся в хорошем соответствии с теоретическими расчетами Ми. В ряде случаев и для неметаллических золей характерна яркая окраска (золи берлинской лазури, гидроксида железа (III), сульфида сурьмы), интенсивность которой заметно снижается при понижении степени дисперсности. 2. Молекулярно-кинетические Броуновское движение В 1827 г. английский ботаник Р. Броун заметил, что частицы цветочной пыльцы, взвешенные в воде, находящиеся в поле зрения микроскопа, непрерывно двигаются по сложным траекториям, не оставаясь ни на мгновение в покое. Только в 1905 г. А. Эйнштейн на основе законов статистической механики дал точную количественную теорию броуновского движения. Известно, что фундаментальные исследования Л. Больцмана, заложившие основу статистической физики, отвергались многими крупнейшими физиками того времени. Теория броуновского движения, созданная Эйнштейном, подтвержденная экспериментально, продемонстрировала полную достоверность основных положений Л. Больцмана. Не меньшую роль здесь сыграли теоретические исследования М. Смолуховского, которые отличались от работ А. Эйнштейна лишь несколько меньшей строгостью, но были более наглядны. В ходе теоретических исследований диффузии взвешенных в жидкости шаров малой величины (модель глобулярных коллоидных частиц) А. Эйнштейн вывел формулу
где D – коэффициент диффузии; r – радиус частицы; N – число Авогадро; h – коэффициент вязкости дисперсионной среды. Как видно из формулы, коэффициент диффузии зависит от Т, вязкости и размеров частицы. Коллоидная частица перемещается в результате столкновений и постоянно меняет направление и скорость. Она претерпевает в воздухе 1016столкновений в секунду, а в воде – 1020. По расчетам Смолуховского, она при этом приобретает скорость порядка 102‑104см/сек. Соединяя прямыми линиями положение частицы в поле наблюдения через определенные, но равные промежутки времени, мы получим проекцию сдвига частицы (рис. 2.1). Каждый отрезок этой ломаной есть проекция сдвига частицы за время наблюдения.
Рис. 2.1. Проекция сдвига частицы Для расчета величины сдвига за время t используют средне-квадратичную величину смещения (сдвига) `х2:
где х1, х2, хn– отдельные наблюдаемые смещения частицы, n – число смещений. А. Эйнштейном получена формула, связывающая коэффициент диффузии со среднеквадратичной величиной сдвига:
Сопоставим (2.1) и (2.3) и получим:
И далее:
Формула (2.5) позволяет определить число Авогадро по результатам измерения частных значений величин сдвига, коэффициента вязкости и размера частиц. Формулы А. Эйнштейна были подтверждены Ж. Перреном и его учениками Они наблюдали за движением частиц с помощью микроскопа и регистрировали их положения через равные промежутки времени. Подставив полученные значения в формулу (2.5), они получили величину N, близкую к действительной. Он, кроме того, подверг экспериментальной проверке формулу (2.4), исследовав величину сдвига частиц в коллоидных растворах золота с частицами величиной r, равной 27 и 52 нм, и подтвердил ее. Формула (2.1) также была подвергнута экспериментальной проверке. Так, при постоянной температуре изменяли вязкость дисперсионной среды. В этом случае величина сдвига
где Формула была подтверждена при различных соотношениях t/h, а также при различных значениях длительности наблюдений. На основе экспериментальных данных (измерений Т, определения вязкости и величины сдвига) были вычислены размеры коллоидных частиц. Долгое время существование молекул и атомов, которые нельзя было наблюдать и представления о которых вводились молекулярно-кинетической теорией, отрицалось. Например, физико-химик В. Оствальд утверждал, что эти частицы являются лишь удобной "фикцией", которая дает возможность получать полезные результаты. Теория коллоидных растворов со всеми ее выводами и уравнениями, в основе которых лежат молекулярно-кинетические представления, получила полное экспериментальное подтверждение. Эти частицы можно было видеть, подсчитать количество, определить скорость их движения, величину и частоту флуктуаций. Таким образом была доказана достоверность основных предпосылок и выводов молекулярно-кинетической теории на отдельных частицах. 2.2. Кинетическая устойчивость дисперсионных Кинетическая устойчивость любой дисперсионной системы зависит от интенсивности теплового движения и силы земного притяжения частиц, которая определяется их массой. Согласно классическим термодинамическим представлениям, все частицы, плотность которых превышает плотность дисперсионной среды, должны были бы осесть на дно сосуда. В действительности они в соответствии с теорией броуновского движения распределяются по высоте по так называемому гипсометрическому (барометрическому) закону. В результате указанных выше факторов (интенсивность теплового движения, сила земного притяжения) устанавливается стационарное состояние. При этом молекулы распределяются по высоте по гипсометрическому закону:
где N – число Авогадро; m – масса частицы; g – ускорение силы тяжести; C1 и C2– концентрации молекул (частиц) на высоте h1 и h2соответственно. Для распределения частиц в жидкости необходимо в уравнение (2.6) ввести поправку на уменьшение веса частиц, погруженных в жидкость, в соответствии с законом Архимеда (r‑rо)/r, где r – плотность дисперсной фазы, rо– плотность дисперсионной среды. Для коллоидных растворов удобнее в уравнении (2.6) заменить соотношение C1/C2 на n1/n2, где n1и n2– концентрация, выраженная числом частиц в единице объема. В результате уравнение (2.6) принимает вид:
Уравнения (2.6) и (2.7) позволяют вычислить, на какой высоте концентрация частиц изменится в заданное количество раз. Например, для воздуха высота h2, на которой концентрация кислорода уменьшится вдвое, составляет 5 км. На высоте 100 км концентрация уменьшится в 106раз. Для количественной оценки кинетической неустойчивости дисперсных систем используется критерий: Этот критерий показывает, как быстро происходит относительное изменение концентрации частиц по высоте, т.е. характеризует кинетическую неустойчивость системы. После несложных преобразований из (2.7) можно получить:
где no– число частиц в единицах объема на фиксированной высоте ho. После дифференцирования получим:
При увеличении радиуса частиц в 100 раз величина d ln n/dh увеличивается в 1 000 000 раз. Таким образом, устойчивость одной и той же системы в пределах коллоидной степени дисперсности (1‑100 нм) может различаться в миллион раз. Из (2.9) следует: чем меньше разность плотностей дисперсной фазы и дисперсионной среды (r – rо), тем больше кинетическая устойчивость системы. Если плотности равны r = rо, то d ln n/dh обращается в нуль, т.е. концентрация дисперсной фазы не изменяется по высоте. В этом случае система абсолютно кинетически устойчива. Если плотности дисперсной фазы меньше плотности дисперсионной среды r< rо, то r – rо< 0 и соответственно d ln n/dh > 0, это означает, что частицы будут всплывать, т.е. концентрация увеличивается по высоте, например, концентрация частичек жира в молоке. Уравнения (2.7)-(2.9) характеризуют стационарное состояние дисперсной системы, которое получило название седиментационное равновесие. Для того, чтобы система пришла к этому состоянию, необходимо некоторое время, зависящее от скорости оседания (или всплывания) частиц. По формуле Стокса скорость U оседания частиц равна:
Расчеты по уравнению Стокса показывают, что для частиц с плотностью r @ 10 г/см3и плотностью дисперсионной среды r = 1 г/см3при вязкости среды h = 0,0015 Па ´ сек частицы с радиусом 100 нм проходят путь в 1 см – за 5,86 сек, с радиусом 10 нм – за 16 часов, а с радиусом 1 нм – за 19 лет. Установление равновесия требует сохранения состояния покоя и постоянства температуры, чтобы избежать появления конвективных потоков. Для того, чтобы ускорить оседание частиц, используются ультрацентрифуги, которые позволяют заменить силы земного притяжения центробежной силой. Эта сила может превышать силу земного притяжения в 1 000 000 и более раз. Наряду с ускорением процесса использование ультрацентрифугирования позволяет определить средний размер коллоидных частиц, распределение их по размерам и даже качественно оценить отклонение частиц от сферической формы. Осмотическое давление А. Эйнштейн на основе расчетов показал, что в сильно разбавленном растворе молекулы и взятые в равном количестве микроскопические частицы создают одинаковое осмотическое давление П. Но при равных массовых концентрациях за счет значительно больших в сравнении с молекулами размеров коллоидных частиц осмотическое давление коллоидных растворов значительно меньше. Действительно, в разбавленном идеальном растворе П = CRT = 1/3nmU2, (2.11) где С – концентрация растворенного вещества (моль/л); m – масса частиц; n – число частиц; U2– средняя квадратичная скорость. Для двух различных растворов по уравнению (2.11) можно записать: П1 = 1/3 n1m1`U21 ; П2= 1/3 n2m2`U22 . Очевидно, что при одинаковой температуре m1U21 = m2U22,
Поскольку линейные размеры коллоидных частиц обычно на 2‑3 порядка больше линейных размеров молекул, то при одинаковых весовых концентрациях количество частиц в единице объема коллоидных растворов будет на 6-9 порядков меньше чем в истинных растворах; во столько же раз будет меньше и осмотическое давление. Практически измерение осмотического давления используют лишь для определения величин частиц высокомолекулярных соединений, которые в отличие от типичных коллоидов являются сравнительно концентрированными (например, Fe(OH)3, V2O5; Al2O3, SiO2). Их агрегаты образуют рыхлые губчатые структуры и связывают большой объем жидкости. Поэтому для расчета их осмотического давления формула (2.11) несколько скорректирована:
где CB– весовая концентрация, М – молярная масса, Nc– доля растворителя, связанная с коллоидными частицами. Равновесие Гиббса-Доннана Для систем, в состав которых входят высокомолекулярные электролиты, диффузии которых препятствует мембрана и низкомолекулярные электролиты, процесс диффузии в целом протекает необычно. Эта особенность, приводящая к неравномерному распределению низкомолекулярных электролитов, получила теоретическое обоснование в работах Доннана. Рассмотрим типичную модель системы, содержащие полиэлектролит и раствор низкомолекулярного электролита. Пусть это будет золь, отделенный от раствора низкомолекулярного электролита мембраной, непроницаемой для полиэлектролита и проницаемой для низкомолекулярного электролита. Такими полиэлектролитами могут быть белки, нуклеиновые кислоты. Пусть полиионы R-несут отрицательный заряд, а противоположно заряженный Na+является общим для ВМС (высокомолекулярных соединений) и НМС (низкомолекулярных соединений). Чтобы упростить расчет примем, что объемы А и Б двух частей системы равны и равны единице, а С1.и С2 – исходные концентрации. Начальное состояние такой системы будет следующим:
Из условия сохранения электронейтральности через мембрану должно пройти в любом направлении равное количество отрицательно и положительно заряженных ионов. Поскольку ионы R-не могут диффундировать через мембрану, возможна только диффузия ионов Na+и Cl-из части Б в часть А. Диффузия будет протекать до тех пор, пока не установится равновесие, изображенное схемой:
где х – количество продиффундировавших ионов Na+и Cl-. Если считать, что коэффициент диффузии ионов Na+и Cl- через мембрану в обоих направлениях одинаков, то для момента равновесия можно записать: для ионов натрия
для ионов хлора
где k1и k2– коэффициент пропорциональности. Перемножив почленно левые и правые части уравнений, после преобразований получим:
Из уравнения (2.6) следует, что при очень малой концентрации коллоидов (полиионов) в части системы А, когда С1значительно меньше, чем С2, т.е. С1<<С2, в знаменателе можно пренебречь величиной С1. В этом случае получим:
Это значит, что при малой концентрации коллоидов низкомолекулярный электролит равномерно распределится по всему объему, по обе стороны мембраны. Наоборот, очень большая концентрация полиионов в левой части системы будет препятствовать диффузии, HMC – ионов Na+и Cl-из правой части системы в левую. Действительно, если С1>> С2, то в знаменателе можно пренебречь членом 2С2 и получим:
Если в состоянии равновесия при С1> С2ввести хлорид натрия в левую часть системы, то равновесие нарушится и ионы Na+и Cl-в соответствии со вторым законом термодинамики будут диффундировать в правую часть системы, т.е. от меньшей концентрации к большей. Равновесие Доннана имеет большое биологическое значение. Так, в плазме крови содержится 7-9 % белков. Однако кровь непосредственно не соприкасается с клетками. С ними соприкасается лимфа, заполняющая межклеточное и межтканевое пространство. Солевой состав лимфы почти не отличается от крови, но содержание белков в лимфе всего 0,01-0,03%. Именно поэтому в соответствии с (2.3) при введении соли в кровяную плазму лишь малая часть ее переходит в клетку, в которой поддерживается стабильный солевой состав. 2.5. Электрические свойства коллоидных Возникновение электрического заряда на поверхности играет чрезвычайно большую роль в физической химии дисперсных систем и поверхностных явлений. Явления, связанные с взаимодействием электрического поля с зарядом жидкости или с поверхностным зарядом диспергированных частиц твердого тела, получили название электрокинетических. Движение жидкости относительно стенок твердых тел при наложении электрического поля получило название электроосмос. Движение твердых частиц под воздействием электрического поля названо электрофорез. Оба эти явления были впервые открыты и описаны в 1809 г. профессором МГУ Ф.Ф.Рейсом. Если в нижнюю зону U-образной трубки поместить пористое тело или пучок большого числа стеклянных капилляров, заполнить оба колена U-образной трубки сильно разбавленным водным раствором электролита и пропускать ток, то жидкость будет перемещаться из одного колена в другое, т.е. будет осуществлять явление электроосмоса. Если пористая масса – стекло, то вода будет перемещаться к катоду. Объясняется это тем, что поверхность стекла адсорбирует гидроксид-ионы. В водном растворе остаются свободные ионы гидроксония, которые двигаются по направлению к катоду, увлекая за собой полярные молекулы воды. Электрофорез в опытах рейса был осуществлен следующим образом: частицы диспергированной в воде глины передвигались при наложении электрического поля к аноду. Следовательно, частицы глины несут отрицательный заряд. Диспергированные частицы приобретают заряд вследствие избирательной адсорбции ионов. Строение коллоидных частиц Рассмотрим строение коллоидных частиц на примере коллоидного раствора иодида серебра, приготовленного из растворов AgNO3и KI при избытке AgNO3. Твердая частица – ядро коллоидной частицы – кристаллы иодида серебра (AgJ)n(рис. 2.2). Поверхность ядра адсорбирует преимущественно ионы Ag+, входящие в состав кристалла ядра, приобретая положительный заряд. Обозначим количество ионов Ag+, адсорбированное ядром, через n. Это количество входит в состав ядра. К заряженному ядру притягиваются противоионы NO3-, формируя двойной электрический слой. Часть противоионов n-x находится в адсорбционном слое, которые вместе с ядром составляют частицу, или гранулу. Остальная часть противоионов (х) находится в свободном объеме раствора. Пунктиром изображена линия, замыкающая весь объем
Рис. 2.2 Схема строения коллоидной частицы
электролита, в котором находятся противоионы. Ядро вместе с адсорбционным слоем и слоем свободной жидкости, в которой находятся противоионы, называется мицеллой. В коллоидной химии принята такая форма записи строения мицеллы:
Эта формула соответствует схеме коллоидной частицы, изображенной на рис. 2.2. |
|

 , (1.5)
, (1.5) , (1.6)
, (1.6) . (1.7)
. (1.7)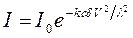 , (1.8)
, (1.8) , (2.1)
, (2.1)
 , (2.2)
, (2.2) . (2.3)
. (2.3) . (2.4)
. (2.4) . (2.5)
. (2.5) ,
, – величина постоянная.
– величина постоянная. , (2.6)
, (2.6) . (2.7)
. (2.7) , где n – число частиц в единице объема.
, где n – число частиц в единице объема.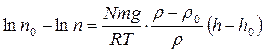 , (2.8)
, (2.8) . (2.9)
. (2.9)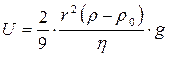 . (2.10)
. (2.10)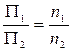 . (2.12)
. (2.12) , (2.13)
, (2.13) , (2.14)
, (2.14) , (2.15)
, (2.15) . (2.16)
. (2.16) . (2.17)
. (2.17) . (2.18)
. (2.18)

