|
|
Работа со строковыми переменными.Вариант№1 1.Дан текст. Заменить пробелами все цифры; 2.Проверить, имеется ли в заданном тексте баланс открывающих и закрывающих скобок. Вариант№2 1. Дан текст. Заменить пробелами все гласные буквы; 2. Для встречающихся в заданном тексте пар рядом расположенных символов указать, сколько раз встречается каждое из таких двухбуквенных сочетаний. Вариант№3 1.Дан текст. Заменить пробелами буквы от «а» до «d» и от «k» до «n»; 2. Отредактировать предложение, удаляя из него лишние пробелы, оставляя только по одному пробелу между словами; Вариант№4 1. Дан текст. Заменить пробелами все знаки препинания; 2.В заданном предложении указать слово, в котором доля гласных (А, Е, I, О) максимальна; Вариант№5 1.Дан текст. Заменить пробелом последнюю букву каждого слова; 2. Для каждого символа заданного текста указать, сколько раз он встречается в тексте. Сообщение об одном символе должно печататься не более одного раза; Вариант№6 1. Дан текст. Заменить пробелом вторую букву каждого слова ; 2. Для каждого слова заданного предложения указать долю согласных. Определить слово, в котором доля согласных максимальна; Вариант№7 1. Дан текст. Заменить знаком « $ » второе слово; 2. Найти самое длинное симметричное слово заданного предложения, например АККА; Вариант№8 1.Дан текст. Заменить пробелами слово, введённое пользователем. В противном случае вывести сообщение о том, что его нет; 2. В заданном предложении найти самое короткое и самое длинное слова; Вариант№9 1. Дан текст. Удалить в нём все цифры; 2. Отредактировать заданное предложение, заменяя многоточие точкой; Вариант№10 1. Дан текст. Удалить в нём все гласные; 2. Из заданного текста предложения выбрать и напечатать только те символы, которые встречаются в нём только один раз (в том порядке, в котором они встречаются в тексте); Вариант№11 1. Дан текст. Удалить в нём третью букву каждого слова; 2. В заданном тексте заменить последовательность символов Х(I) на А(I) и подсчитать число произведённых замен; Вариант№12 1. Дан текст. Удалить в нём буквы от «d» до «h» и все запятые; 2. В заданном тексте удалить символ «,» и подсчитать число удаленных символов. Вариант№13 1. Дан текст. Удалить в нём каждую вторую букву от «b» до «d»; 2. Из текста выбрать числа и записать в массив N. Количество чисел не более 10. Вариант№14 1. Дан текст. Удалить в нём все слова заканчивающиеся на открытый слог; 2. Удалить из текста символы « » и подсчитать длину сформированного текста. Вариант№15 1. Дан текст. Вставить в него после второго слова текст В( заданный с клавиатуры); 2.В тексте предложения заменить символы « » символами «,». Конечные символы удалить, не заменяя на запятые. Определить длину предложения. Если в тексте встречаются несколько символов « » подряд, то вместо них поставить одну запятую. Вариант№16 1. Дан текст. Вставить в него точку после каждого второго слова; 2. Дан текст. Составить программу вычисляющую является ли текст перевёртышем. Вариант№17 1. Дан текст. Вставить в него знак «+» после каждого третьего символа; 2. Дан текст. Составить программу, формирующую текст, составленный из слов текста расположенных в обратном порядке. Вариант№18 1. Дан текст. Вставить в него до и после каждого числа кавычки; 2. Составить программу, формирующую текст, составленный из исходного, где поменяны местами соседние гласные, если такие есть. Вариант№19 1. Дан текст. Вставить в него после каждого слова его первую букву; 2. Составить программу, формирующую текст, составленный из исходного, где поменяны местами две ближайшие буквы от «s» до «w» попарно. Вариант№20 1. Дан текст. Вставить в него после каждого слова его длину; 2. Дан текст. Начиная с i позиции перевернуть его (т.е. записать в нём буквы от последней до i-той наоборот). Вариант№21 1. Дан текст. Подсчитать в нем количество знаков препинания; 2. Составить программу вычисляющую делится ли натуральное число на 3 по признаку делимости. Вариант№22 1. Дан текст. Подсчитать в нем количество заглавных букв; 2. Составить программу вычисляющую является ли введённое число числом Армстронга( число равно сумме его цифр взятых в степени количества цифр); Вариант№23 1. Дан текст. Подсчитать в нем количество всех гласных; 2. Составить программу вычисляющую является ли число не меньше суммы квадратов его цифр; Вариант№24 1. Дан текст. Подсчитать в нем количество предложений и слов; 2. Составить программу, вычисляющую произведение каждых двух последовательных цифр числа. Вариант№25 1. Дан текст. Подсчитать в нем количество чисел; 2. Составить программу, вычисляющую процентное соотношение согласных, гласных букв текста и знаков препинания (включая пробелы). Вариант№26 1. Дан текст. Подсчитать в нем количество гласных, приходящихся на нечётные позиции; 2. Найти произведение количества букв от «a» до «f» на числа, встречающиеся в тексте. Вариант№27 1. Дан текст. Подсчитать в нем количество букв от «g» до «k» каждого слова; 2. Составить программу, определяющую номер дня недели по его названию, (первого, встречающегося в тексте). Вариант№28 1. Составить программу, вычисляющую сумму цифр числа большего, чем 15; 2. Дано 2 текста. Определить являются ли все символы второго текста, символами первого учитывая, что каждый символ первого текста может соответствовать только одному символу второго текста и первый текст может быть больше второго. Вариант№29 1. Составить программу, вычисляющую является ли четырёхзначное число счастливым; 2. Дано 2 текста. Определить, входят ли все символы второго текста в символы первого, учитывая, что порядок их следования сохраняется.
Вариант№30 1. Составить программу вычисляющую состоит ли число из чётных цифр; 2. Определить находятся ли в заданном тексте слова перевертыши, и вывести их на экран.
Лабораторная работа №8. Составление программ, использующих процедуры и функции пользователя. Вариант №1 1.Написать программу решения следующей задачи: Определить периметры трёх треугольников, если заданы координаты их вершин. 2. Написать программу решения следующей задачи: Ввод массивов и матриц осуществлять из файла данных, а их обработку в одной подпрограмме. Вычислить 3.Написать подпрограмму для замены в массиве Y(50) всех чётных элементов на значение 1. 4. Используя нестандартные функции, составить программы для расчёта указанных величин. Вариант №2 1.Написать программу решения следующей задачи: Вычислить сумму объёмов трёх шаров и сумму их поверхностей, если известны их радиусы. 2. Написать программу решения следующей задачи: Вычислить 3.Написать подпрограмму для замены знака каждого пятого элемента массива B(100) на противоположенный. 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №3 1.Написать программу решения следующей задачи: Даны четыре пары чисел: A, a, B, b, C, c, D, d, - которые являются соответственно наружными и внутренними радиусами колец. Найти общую площадь этих колец. 2.Написать программу решения следующей задачи: Вычислить и запомнить суммы положительных элементов каждой строки матриц A(6,6) и B(5,5). 3.Написать подпрограмму для вычисления суммы отрицательных элементов массива A(200). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №4 1.Написать программу решения следующей задачи: Заданы координаты трёх точек. Подсчитать сумму их расстояний до начала координат.
2.Написать программу решения следующей задачи: Переписать положительные элементы массивов X(8), Y(10) в массив Z(k) подряд. Запись осуществить в подпрограмме. Вывести на печать все три массива. 3.Написать подпрограмму для расчёта числа положительных элементов массива B(10,20). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №5 1.Написать программу решения следующей задачи: заданы координаты четырёх точек. Подсчитать сумму их расстояний до точки с координатами (a,b). 2.Написать программу решения следующей задачи: Вывести на экран элементы целочисленных матриц N(6,8) и M(4,7), кратные трём. 3.Написать подпрограмму для вычисления куба суммы положительных элементов массива X(15,30). 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №6 1.Написать программу решения следующей задачи: Спадание активности образца происходит по следующему закону: 2.Написать программу решения следующей задачи: Преобразовать массивы X(10), Y(12), расположив в них подряд только положительные элементы. Вместо остальных элементов записать нули. Вывести преобразованные массивы на экран. 3.Написать подпрограмму для расчёта суммы элементов второй строки матрицы M(20,10). 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №7 1.Написать программу решения следующей задачи: Концентрация вещества в реакторе изменяется по закону 2.Написать программу решения следующей задачи: вычислить суммы и количества элементов матриц X(8,6), Y(4,8), значения которых находятся в интервале от a до m. 3.Написать подпрограмму для вычисления суммы элементов пятого столбца матрицы Z(10,20). 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант№8 1.Написать программу решения следующей задачи: Рассчитать суммарную кинетическую энергию пяти частиц, движущихся ср скоростями V1,V2,V3,V4,V5 близким к скорости света C, и имеющих массу соответственно m1, m2, m3, m4, m5. кинетическая энергия в этих условиях вычисляется по формуле: 2.Написать программу решения следующей задачи: Найти наибольшие элементы в массивах X(10), Y(6), Z(11) и их порядковые номера. 3.Написать подпрограмму для отыскания минимального элемента массива X(25). 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №9 1.Написать программу решения следующей задачи: Определить среднюю высоту полёта аэростата, если четыре измерения температуры и давления дали результаты соответственно T1, T2, T3, T4 и P1, P2, P3, P4. барометрическая формула: 2.Написать программу решения следующей задачи: Вычислить 3.Написать подпрограмму для отыскания максимального элемента массива B(20,30) и индексов этого элемента. 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №10 1.Написать программу решения следующей задачи: Найти электрическую ёмкость двухпроводной линии, состоящей их четырёх участков длиной l1, l2, l3, l4, соответственно и с расстоянием между проводами d1, d2, d3, d4. все провода имеют радиус a. Формула емкости линии: 2.Написать программу решения следующей задачи: Найти наименьшие элементы для матриц A(8,6), X(7,9) и номера строк т столбцов, в которых они расположены. 3.Написать подпрограмму для вычисления k!=1*2*3*…*k.
4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №11 1.Написать программу решения следующей задачи: вычислить среднюю скорость, осаждения смеси частиц диаметром от d1 до d2 плотностью от r1 до r2, если скорость осаждения может быть вычислена по формуле 2.Написать программу решения следующей задачи: Вычислить и запомнить количество отрицательных элементов каждого столбца для матриц A(6,8), X(9,9). 3.Написать подпрограмму для замены в матрице A(10,10) всех элементов, стоящих на главной диагонали на число 2. 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №12 1.Написать программу решения следующей задачи: Вычислить сумму объёмов и сумму поверхностей четырёх цилиндров, если для каждого из них известны высота и радиус основания. 2.Написать программу решения следующей задачи: Для каждой из матриц A(6,6) и B(8,8) вычислить сумму и количество положительных элементов, расположенных на главной диагонали и выше её. 3.Написать подпрограмму для вычисления квадрата суммы элементов массива B(100), которые меньше 10. 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №13 1.Написать программу решения следующей задачи: Главный центральный момент инерции тора относительно оси, перпендикулярной к его плоскости, вычисляется по формуле 2.Написать программу решения следующей задачи: найти наименьшие элементы и их порядковые номера для массивов X(N), Y(M), Z(K). 3.Написать подпрограмму для вычисления суммы положительных элементов i-той строки матрицы C(10,20). 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №14 1.Написать программу решения следующей задачи: Ёмкость сферического конденсатора вычисляется по формуле 2.Написать программу решения следующей задачи: Найти целочисленные элементы и номера строк и столбцов, в которых они расположены, для матриц A(5,8), B(6,4). 3.Составить подпрограмму для вычисления количества элементов матриц B(30,30), которые лежат в интервале (2,5). 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №15 1.Написать программу решения следующей задачи: Напряжённость магнитного поля в центре прямоугольного витка с током I рассчитывается по формуле 2.Написать программу решения следующей задачи: вычислить среднее значения и суммы диагональных элементов каждой строки матриц A(N,N) и B(M,M). 3.Составить подпрограмму для расчёта квадратного корня из суммы положительных элементов массива X(m,n). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №16 1.Написать программу решения следующей задачи: Определить сумму объёмов и сумму поверхностей трёх прямоугольных параллелепипедов, если известны их измерения. 2.Написать программу решения следующей задачи: Вычислить и запомнить количества и суммы отрицательных элементов каждой строки матриц C(6,6), D(8,8). 3.Составить подпрограмму для вычисления минимального элемента j-той строки матрицы C(m,n) и номера столбца, в котором находится этот элемент. 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №17 1.Написать программу решения следующей задачи: Главный центральный момент инерции сплошного шара определяется по формуле 2.Написать программу решения следующей задачи: Для каждой из целочисленных матриц A(6,8) и B(5,7) вывести на печать количество элементов, кратных шести, и сами эти элементы. 3.Составить подпрограмму для расчёта количества нулевых элементов массива X(k,n); 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №18 1.Написать программу решения следующей задачи: Ёмкость цилиндрического конденсатора с длиной l и радиусами внутреннего и внешнего цилиндров, равными r1 и r2, вычисляется по формуле 2.Написать программу решения следующей задачи: Вычислить и запомнить суммы положительных элементов каждого столбца матриц A(10,5) и B(6,8) 3.Составить подпрограмму для замены знака вех нечётных элементов массива Z(150) на противоположенный. 4. Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №19 1.Написать программу решения следующей задачи: Вычислить сумму объёмов и сумму полных поверхностей трёх круглых конусов, если для каждого конуса известны высота и радиус основания. 2.Написать программу решения следующей задачи: Для каждой из матриц A(5,5) и B(8,8) вычислить сумму и количество отрицательных элементов, расположенных на главной диагонали и выше её. 3.Составить подпрограмму для вычисления следа (суммы элементов главной диагонали) матрицы B(m,n). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №20 1.Написать программу решения следующей задачи: Главный центральный момент инерции полого шара массой m с радиусами внешней и внутренней поверхностей, равными R1 и R2, вычисляется по формуле 2.Написать программу решения следующей задачи: Для каждой из матриц A(6,6) и B(8,8) найти сумму элементов главной диагонали и сумму элементов побочной диагонали. 3.Составить подпрограмму для замены знака на противоположенный у всех элементов i-ого столбца матрицы B(m,n). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант № 21 1.Написать программу решения следующей задачи: Ёмкость сферического конденсатора вычисляется по формуле 2.Написать программу решения следующей задачи: Переписать в массив X подряд положительные элементы массива Y(10). 3.Составить подпрограмму для вычисления максимального элемента матрицы Z(20,30) и определения номеров строки и столбца. Которым принадлежит этот элемент. 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №22 1.Написать программу решения следующей задачи: Концентрация вещества в реакторе растёт по закону 2.Написать программу решения следующей задачи: Для каждой из матриц X(8,8) и Y(10,10) вычислить сумму элементов, расположенных на главной диагонали и выше её. 3.Составить подпрограмму для вычисления количества элементов массива X(10,25), значения которых больше 10, и вычисления квадратного корня из суммы этих элементов. 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №23 1.Написать программу решения следующей задачи: Найти сумму площадей трёх треугольников, если известны длинны их сторон (для вычисления площади использовать формулу Герона). 2.Написать программу решения следующей задачи: Для каждой из матриц A(N,N) и B(M,M) найти целочисленные элементы верхней треугольной матрицы. 3.Составить подпрограмму для вычисления минимального элемента n-ой строки матрицы C(m,n). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №24 1.Написать программу решения следующей задачи: Главный центральный момент инерции тора относительно оси, лежащей в его плоскости, вычисляется по формуле 2.Написать программу решения следующей задачи: Вычислить 3.Составить подпрограмму для вычисления количества нулевых элементов I-ого столбца матрицы A(m,n). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №25 1.Написать программу решения следующей задачи: Ёмкость цилиндрического конденсатора вычисляется по формуле 2.Написать программу решения следующей задачи: Вычислить и запомнить количества и суммы отрицательных элементов каждого столбца матриц X(10,8), Y(6,8). 3.Составить подпрограмму для вычисления количества элементов массива Y(20,30), лежащих в интервале [0,2]. 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант № 26 1.Написать программу решения следующей задачи: Напряжённость поля, создаваемое точечным зарядом вычисляется по формуле 2.Написать программу решения следующей задачи: Вычислить и запомнить сумму и число положительных элементов каждого столбца матрицы A(10,15) при условии, что aij>0. 3.Составить подпрограмму для расчёта тангенса суммы положительных элементов массива Z(m,n). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №27 1.Написать программу решения следующей задачи: Работа по перемещению заряда в однородном поле вычисляется по формуле 2.Написать программу решения следующей задачи: Вычислить и запомнить суммы и числа элементов каждой строки матрицы A(15,20). Результаты отпечатать в виде двух столбцов. 3.Составить подпрограмму для вычисления максимального и минимального элементов пятого столбца матрицы B(20,15) и определения номеров строк, в которых стоят эти элементы. 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №28 1.Написать программу решения следующей задачи: Ёмкость плоского конденсатора рассчитывается по формуле 2.Написать программу решения следующей задачи: Расположить в массиве R сначала положительные, а затем отрицательные элементы массива Z(30). 3.Составить подпрограмму для замены элементов k-ого столбца матрицы A(n,m) на число 1. 4.Используя нестандартные функции, составить программы для расчёта указанных величин Вариант №29 1.Написать программу решения следующей задачи: Сопротивление рассчитывается по формуле 2.Написать программу решения следующей задачи: Вычислить 3.Составить подпрограмму для расчёта количества нулевых элементов i-ой строки матрицы B(k,m). 4.Используя нестандартные функции, составить программы для расчёта указанных величин
Вариант №30 1.Написать программу решения следующей задачи: Рассчитать среднюю работу по перемещению заряда в однородном поле для трёх зарядов, если для каждого из них известны величина заряда q, напряжённость E, расстояние между двумя точками d. Работа вычисляется по формуле 2.Написать программу решения следующей задачи: Определить число положительных элементов до первого отрицательного в массивах X(16), Y(20), Z(25). 3.Составить подпрограмму для нахождения количества положительных, отрицательных и нулевых элементов массива C(20,30). 4. Используя нестандартные функции, составить программы для расчёта указанных величин
Лабораторная работа №9. |
|
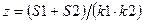 , где S1 и k1 – сумма и количество положительных элементов массива X(10); S2 и k2 – то же для массива Y(12).
, где S1 и k1 – сумма и количество положительных элементов массива X(10); S2 и k2 – то же для массива Y(12).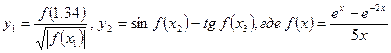
 , где S1 и k1 – сумма и количество элементов массива X(12); S2 и k2 – то же для массива Y(8).
, где S1 и k1 – сумма и количество элементов массива X(12); S2 и k2 – то же для массива Y(8).





 . Определить среднюю активность трёх образцов через заданное время t, если для каждого из них известны начальная активность E0 и константа скорости k.
. Определить среднюю активность трёх образцов через заданное время t, если для каждого из них известны начальная активность E0 и константа скорости k.
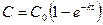 . Определить среднюю концентрацию вещества в трёх реакторах, если для каждого реактора заданы начальная концентрация С0, время реакции t и константа скорости k.
. Определить среднюю концентрацию вещества в трёх реакторах, если для каждого реактора заданы начальная концентрация С0, время реакции t и константа скорости k.


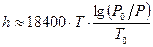 , где P0=760 мм рт. ст., T0=273,15 К.
, где P0=760 мм рт. ст., T0=273,15 К. , где xmax – максимальный элемент массива X(m), ymin – минимальный элемент массива Y(n). вычисления выполнить в одной подпрограмме.
, где xmax – максимальный элемент массива X(m), ymin – минимальный элемент массива Y(n). вычисления выполнить в одной подпрограмме.
 , где e0*e=8,85*10-12 Ф/м.
, где e0*e=8,85*10-12 Ф/м.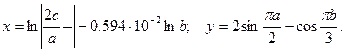

 ; g=9.8 м/с2; m=0,6 Па*с.
; g=9.8 м/с2; m=0,6 Па*с.
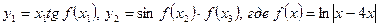 .
. . Найти среднее значение I для трёх торов, если известны для каждого из них масса m, радиус R, и радиус поперечного сечения r.
. Найти среднее значение I для трёх торов, если известны для каждого из них масса m, радиус R, и радиус поперечного сечения r.
 . Здесь r1, r2 – радиусы внутренней и внешней сфер, соответственно. Найти общую ёмкость четырёх параллельно соединённых сферических конденсаторов, если для каждого из них известны значения r1 и r2, а
. Здесь r1, r2 – радиусы внутренней и внешней сфер, соответственно. Найти общую ёмкость четырёх параллельно соединённых сферических конденсаторов, если для каждого из них известны значения r1 и r2, а 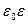 *10-12 Ф/м.
*10-12 Ф/м. .
. , где a и b – длины сторон прямоугольника. Найти напряжённость магнитного поля в общем центре трёх прямоугольных витков , лежащих в одной плоскости. Если для каждого из них известны размеры и значения силы тока I ( ток во всех витках проходит в одном направлении).
, где a и b – длины сторон прямоугольника. Найти напряжённость магнитного поля в общем центре трёх прямоугольных витков , лежащих в одной плоскости. Если для каждого из них известны размеры и значения силы тока I ( ток во всех витках проходит в одном направлении).
 .
. Найти среднее значение I для трёх шаров, если для каждого из них известны масса m и радиус R.
Найти среднее значение I для трёх шаров, если для каждого из них известны масса m и радиус R.
 . Найти общую ёмкость трёх параллельно соединённых цилиндрических конденсаторов, если для каждого из них известны значения l, r1, r2, a
. Найти общую ёмкость трёх параллельно соединённых цилиндрических конденсаторов, если для каждого из них известны значения l, r1, r2, a 

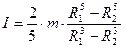 . Найти среднее значение I для трёх полых шаров с известными значениями m, R1, R2.
. Найти среднее значение I для трёх полых шаров с известными значениями m, R1, R2.
 . Здесь r1, r2 – радиусы внутренней и внешней сфер. Найти общую ёмкость трёх последовательно соединённых сферических конденсаторов, если для каждого из них известны значения r1, r2, а
. Здесь r1, r2 – радиусы внутренней и внешней сфер. Найти общую ёмкость трёх последовательно соединённых сферических конденсаторов, если для каждого из них известны значения r1, r2, а 
 .
. . Определить среднюю концентрацию вещества в трёх реакторах, если для каждого известны начальная концентрация вещества C0, время реакции t и константы скоростей k1 и k2.
. Определить среднюю концентрацию вещества в трёх реакторах, если для каждого известны начальная концентрация вещества C0, время реакции t и константы скоростей k1 и k2.
 .
.
 .
. . Найти среднее значение I для четырёх торов, если для каждого из них известны масса m, радиус R и радиус поперечного сечения r.
. Найти среднее значение I для четырёх торов, если для каждого из них известны масса m, радиус R и радиус поперечного сечения r. и
и  где xmax и ymax – максимальные элементы массивов X(20), Y(30); xmin и ymin – минимальные элементы этих же массивов (вычисление максимального и минимально элементов массива вычислять в одной подпрограмме).
где xmax и ymax – максимальные элементы массивов X(20), Y(30); xmin и ymin – минимальные элементы этих же массивов (вычисление максимального и минимально элементов массива вычислять в одной подпрограмме).
 . Здесь l – длинна конденсатора, r1, r2 – радиусы внутреннего и внешнего цилиндров, соответственно. Найти общую ёмкость трёх последовательно соединённых конденсаторов, если для каждого из них известны значения l, r1, r2, а
. Здесь l – длинна конденсатора, r1, r2 – радиусы внутреннего и внешнего цилиндров, соответственно. Найти общую ёмкость трёх последовательно соединённых конденсаторов, если для каждого из них известны значения l, r1, r2, а 
 , где q – заряд создающий поле,
, где q – заряд создающий поле,  ,
, .
. , где q – заряд, E – напряжённость поля, d – расстояние между двумя точками электрического поля. Вычислить общую работу для трёх зарядов, если для каждого из них известны величина заряда q, E и d.
, где q – заряд, E – напряжённость поля, d – расстояние между двумя точками электрического поля. Вычислить общую работу для трёх зарядов, если для каждого из них известны величина заряда q, E и d. .
. , где S – площадь одной пластины, d – расстояние между пластинами. Рассчитать среднюю ёмкость для трёх конденсаторов, если для каждого из них заданы S и d, а
, где S – площадь одной пластины, d – расстояние между пластинами. Рассчитать среднюю ёмкость для трёх конденсаторов, если для каждого из них заданы S и d, а  . Где
. Где  - удельное сопротивление проводника, l – длина проводника, S – площадь поперечного сечения. Рассчитать общее сопротивление для четырёх проводников, если для каждого заданы свои l, S,
- удельное сопротивление проводника, l – длина проводника, S – площадь поперечного сечения. Рассчитать общее сопротивление для четырёх проводников, если для каждого заданы свои l, S,  , где s1 – сумма положительных элементов массива X(15); s2 – сумма отрицательных элементов массива Y(20)
, где s1 – сумма положительных элементов массива X(15); s2 – сумма отрицательных элементов массива Y(20)

 .
.