|
|
Программирование рекурсивных процедур.Вариант №1 1.Вычислить значение функции
2.Дано арифметическое выражение, содержащее три вида скобок "(", "[", "{" Проверить правильность расстановки скобок; если какая-то скобка не имеет парной, напечатать, какая именно. Вариант №2 1.Вычислить значение функции, используя рекурсию. S
2.Студенты двух групп имеют порядковые номера от 1 до N в каждой группе. В процедуре Р_1 функцией Random определяются два числа «а» и «b» от 1 до N. Если числа разные, то два участника с номерами «а» и «b» выбывают, оставшиеся ученики перенумеровываются от 1 до (N-1) и играют дальше (процедура Р_1 повторяется с новыми значениями «а» и «b»), иначе выводится значение совпавшего номера, ученики получают приз и процедура Р_2 предлагает играть снова.
Вариант №3 1.Вычислить значение С
2.На карте местности имеется N населенных пунктов, пронумерованных от 1 до N (N x 10). Некоторые из пунктов соединены между собой дорогами. Информация о дорогах задается в виде последовательности пар чисел i, j (i<j), указывающих, что i-й и j-й пункты соединены дорогой, признак конца этой последовательности — пара нулей. Определить, можно ли попасть по этим дорогам из первого пункта в n-й. Вариант №4
1.Извлечь корень m-ой степени из числа
2.Организовать рекурсивный алгоритм так называемой "быстрой сортировки" Хоара: имеются два указателя i и j, причем вначале i = 1, а j = N (номер последнего элемента). Сравним a[i] и a[j], и если обмен не требуется, то уменьшим j на 1 и повторим этот процесс. После первого обмена увеличим i на 1 и будем продолжать сравнения, увеличивая i, пока не произойдет еще один обмен. Тогда снова уменьшим j и т.д., то есть будем "сжигать свечку с обоих концов", пока не станет i = j'. В результате получим, что слева от a[i] оказались только меньшие элементы, а справа — только большие (тем самым элемент а[i] окажется на своем окончательном месте), после чего рекурсивно применить этот же метод длялевой и правой частей массива до тех пор, пока в подмассиве не останется только один элемент. Вариант №5
1.Вычислить sin
2.Даны целые неотрицательные числа m, n. Вычислить так называемую "функцию Аккермана":
Вариант №6 1.Вычислить элементы последовательности, используя рекурсию. P0(x)=1, P1(x)=x, Pm(x)=
2.Вычислить значение функции, используя рекурсию.
Вариант №7
1.Вычислить
2.Напишите рекурсивную процедуру для вычисления значения полинома Лежандра порядка n в точке x. Полиномы Лежандра определяются следующим образом: P0 (x) = 1, P1 (x) = x,
Вариант №8
1.Вычислить значение функции, используя рекурсию.
2.Дана строка текста, оканчивающаяся точкой. Напечатать этот текст в обратном порядке, используя рекурсию.
Вариант №9 1.Вычислить значение функции, используя рекурсию.
2.Составить рекурсивную программу вычисления определителя N-гo порядка (N < 5), пользуясь формулой разложения определителя по i-й строке и зная формулу вычисления определителя 2-го порядка. Вариант №10 1.Вычислить значение функции, используя рекурсию.
2.Организовать вычисление N! с помощью рекурсивной функции. Какой алгоритм работает быстрее: рекурсивный или нерекурсивный? Почему? Вариант №11
1.Вычислить значение функции, используя рекурсию.
C помощью этого ряда найти ln2, ln3, ln4.
2.Составить рекурсивную программу нахождения корня заданной функции F(x) в интервале [а, b] методом деления отрезка пополам с заданной точностью Е. Вариант №12
1.Вычислить элементы последовательности, используя рекурсию. T0(x)=1, T1(x)=x,
Tk+1(x)=2xTk(x)-Tk-1(x) для k
2.Рассчитать число зёрен, выращенных крестьянином за N лет, если он посадил 10 зёрен, а годовой урожай составляет 22 зерна на каждое посаженное зерно.
Вариант №13
1.Вычислить элементы последовательности, используя рекурсию. P0(x)=1, P1(x)=x, Pk(x)=[(2k-1)xTk-1(x)-(k-1)Tk-2(x)]/2 для k
2.Рассчитать число золотых монет, принесённых в дань господину, если N+1 подданных последовательно передают монеты от первого к последнему. Причём, первый отдаёт одну монету, второй увеличивает число монет вдвое, третий – в три раза и т.д. Вариант №14
1.Вычислить элементы последовательности, используя рекурсию. L0(x)=1, L1(x)= kLk(x)=(-x+2k+ для k=2,3,… 2.Рассчитать функцию y=sin(sin(sin(…(sin(x))))), в которой имя функции «sin» повторяется n раз. Вариант №15
1.Рассчитать число рыб, выращенных в аквариуме за N лет, если вначале было две рыбы, а число рыб увеличивается пропорционально числу лет, т.е. 4, 12, 48 и т.д. 2.Функция Аккермана определяется следующим образом: A (0, y) = y + 1, A (x, 0) = A (x – 1,1), A (x, y) = A (x – 1, A (x, y – 1)). Здесь х, у – целые неотрицательные числа. Функция возрастает настолько быстро, что вскоре «выбивает» из работы любой компьютер. Определим «модулярную функцию Аккермана» как A mod m, где значение параметра m вводится. Постройте таблицу значений этой функции. Вариант №16
1.Вычислить числовую последовательность
2.Рассчитать функцию y=a/(b+(a/(b+(a/(b+(…+a/b)))))), в которой знак деления «/» повторяется N раз.
Вариант №17
1.Вычислить числовую последовательность, используя рекурсию.
( 2.Составить рекурсивный алгоритм нахождения N-ro числа Фибоначчи: 0, 1, 1, 2, 3, 5, 8, ..., то есть каждое последующее число равно сумме двух предыдущих. Вариант №18
1.Возведение в степень числа (без использования указателей), с использованием рекурсии.
2.Вычислить значение функции, используя рекурсию.
Вариант №19 1.Вычислить значение функции, используя рекурсию. S(x)=
2.Рассчитать количество студентов, выпущенных университетом за N лет, если в среднем на первый курс поступает 2000 абитуриентов, а до пятого курса доходит каждый третий. Вариант №20 1.Вычислить
2.Даны действительное число А, целоечисло n. Организовать вычисление Ап с помощью рекурсивной функции. Показатель степени n может быть любым целым числом. Вариант №21 1.Создать программу, в которой рекурсивная функция используется для суммирования целых чисел от 1 до n , где n введенное пользователем число, большее или равное 1.
2.Найти значение функции, используя рекурсию.
Вариант №22 1.Вычислить элементы последовательности, используя рекурсию. H0(x)=1, H1(x)=2x,
Hk+1(x)=2xHk(x)-2kHk-1(x) для k
2. Описать рекурсивную функцию pow(x, n) от вещественного x (x <> 0) и целого n, которая вычисляет величину xn согласно формуле
Вариант №23
1.Программа вычисления значения функции целочисленного аргумента, рекурсивное определение которой имеет вид:  N-3, если N>23, F(N)= F(F(n+4)), если N<=23. N-3, если N>23, F(N)= F(F(n+4)), если N<=23. 2.Составить рекурсивную программу вычисления НОД (наибольшего общего делителя), основанную на соотношении НОД(n, т) = НОД(m, r), где r — остаток от деления n на т. Вариант №24 1.Напишите рекурсивную процедуру для решения уравнений вида F (x) = x методом простых итераций. Проверьте её работу на функциях Cos(x) и Sqrt(x+1). 2.Вычислить элементы последовательности N0(x)=1, N1(x)=x, Nk(x)=
Вариант №25 1.Вычислить элементы последовательности R0(x)=1, R1(x)=x, Rn+1(x)=x+x(1-Rn(x))+(1-Rn-1(x))2 для n
2.Вычислить значение функции, используя рекурсию.
Вариант №26 1.Вычислить элементы последовательности N0(x)=1, N1(x)=x, Na(x)=
2.Требуется рассчитать число осколков, полученных в результате деления за n миллисекунд, если каждый осколок делится на два за одну миллисекунду.
Вариант №27 1.Вычислить значение функции, используя рекурсию.
2.Определить максимальный элемент в массиве, используя рекурсивную процедуру для поиска максимума. Вариант №28
1.Вычислить значение функции, используя рекурсию.
2.Разложить заданное число на всевозможные слагаемые, использованием рекурсии. Вариант №29
1.Вычислить значение функции, используя рекурсию. H(x)=
2.Запрограммируйте с использованием рекурсии вычисление функции F (x) = xn. Вариант №30
1.Вычислить элементы числовой последовательности, используя рекурсию. A0(x) = 1 A1(x) = x
2.Рассчитать значение последовательности, заданной следующим образом: a (1) = 1, a (n) = n – a (a (n – 1)), n>1.
Лабораторная работа №12. |
|




 с помощью разложения
с помощью разложения



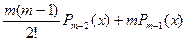
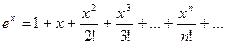
 на основе формулы
на основе формулы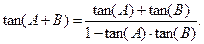



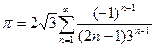


 2.
2. +1-x,
+1-x, =
= 
 , n
, n  =1-
=1-  +
+ 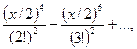




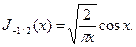
 определить как константу, заменой переменных перейти к целому представлению индексов).
определить как константу, заменой переменных перейти к целому представлению индексов).

 и
и  на основе равенств
на основе равенств









