|
|
Динамика вращательного движения твердого тела вокругНеподвижной оси
Момент силы
где Момент инерции относительно оси вращения: а) материальной точки
J=mr2,
где т - масса точки; r - ее расстояние от оси вращения; б) дискретного твердого тела
где Δmi - масса i-го элемента тела; ri - расстояние этого элемента от оси вращения; п - число элементов тела; в) сплошного твердого тела
Если тело однородно, т. е. его плотность ρ одинакова по всему объему, тоdm=ρdV, и
где V - объем тела. Теорема Штейнера. Момент инерции тела относительно произвольной оси
J=J0+ma2,
где J0 - момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; а - расстояние между осями; m - масса тела. Момент импульса вращающегося тела относительно оси
Закон сохранения момента импульса
где
Таблица 2 - Моменты инерции тел правильной геометрической формы
Закон сохранения момента импульса для двух взаимодействующих тел
где Закон сохранения момента импульса для одного тела, момент инерции которого меняется,
где J1 и J2 - начальный и конечный моменты инерции; ω1 и ω2 - начальная и конечная угловые скорости тела. Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси
где Если момент силы и момент инерции постоянны, то это уравнение записывается в виде
В случае постоянного момента инерции основное уравнение динамики вращательного движения принимает вид
где e - угловое ускорение. Работа постоянного момента силы М, действующего на вращающееся тело
A=Mj,
где j - угол поворота тела. Мгновенная мощность, развиваемая при вращении тела
N=M
Кинетическая энергия вращающегося тела
Кинетическая энергия тела, катящегося по плоскости без скольжения
где vС - скорость центра масс тела;
Силы в механике
Закон всемирного тяготения
где F - сила взаимного притяжения двух материальных точек; m1 и m2 - их массы; r - расстояние между точками; G - гравитационная постоянная. В написанной форме закон всемирного тяготения можно применять и к взаимодействию шаров, масса которых распределена сферически-симметрично. В этом случае r есть расстояние между центрами масс шаров. Напряженность гравитационного поля
где F - сила тяготения, действующая на материальную точку массы m, помещенную в некоторую точку поля. Напряженность гравитационного поля, создаваемого планетой, массу М которой можно считать распределенной сферически-симметрично
где r - расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты. Ускорение свободного падения на высоте h над поверхностью Земли
где R - радиус Земли; g - ускорение свободного падения на поверхности Земли. Если
Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2 (шаров с массой, распределенной сферически симметрично), находящихся на расстоянии r друг от друга
(Потенциальная энергия бесконечно удаленных друг от друга материальных точек принята равной нулю.) Относительная деформация при продольном растяжении или сжатии тела
где ε - относительное удлинение (сжатие); x – абсолютное удлинение; l – начальная длина тела. Напряжение нормальное
где Fynp - упругая сила, перпендикулярная поперечному сечению; S - площадь этого сечения. Закон Гука для продольного растяжения или сжатия
где k - коэффициент упругости (в случае пружины - жесткость); Е – модуль Юнга. Потенциальная энергия растянутого или сжатого стержня
где V - объем тела.
Релятивистская механика В специальной теории относительности рассматриваются только инерциальные системы отсчета. Во всех задачах считается, что оси у, у' и z, z' сонаправлены, а относительная скорость v0 системы координат К' относительно системы К направлена вдоль общей оси хх'. Релятивистское (лоренцево) сокращение длины стержня
где l0 - длина стержня в системе координат К', относительно которой стержень покоится (собственная длина); l - длина стержня, измеренная в системе К, относительно которой он движется со скоростью v; с - скорость распространения электромагнитного излучения. Релятивистское замедление хода часов
где Δt0 - интервал времени между двумя событиями, происходящими в одной точке системы K', измеренный по часам этой системы (собственное время движущихся часов); Δt - интервал времени между двумя событиями, измеренный по часам системы K. Релятивистское сложение скоростей
где v' - относительная скорость (скорость тела относительно системы K'); v0 - переносная скорость (скорость системы K' относительно К), v - абсолютная скорость (скорость относительно системы К). В теории относительности абсолютной скоростью называется скорость тела в системе координат, условно принятой за неподвижную. Релятивистская масса
где m0 - масса покоя; β - скорость частицы, выраженная в долях скорости света ( Релятивистский импульс
Полная энергия релятивистской частицы
где Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если v<<с. Связь полной энергии с импульсом релятивистской частицы
Связь кинетической энергии с импульсом релятивистской частицы
Механические колебания
Уравнение гармонических колебаний
где x - смещение колеблющейся точки от положения равновесия; t - время; А, ω, φ - соответственно амплитуда, угловая частота, начальная фаза; Угловая частота колебаний
где ν и Т - частота и период колебаний. Полная энергия материальной точки, совершающей гармонические колебания,
Период колебаний тела, подвешенного на пружине (пружинный маятник)
где m - масса тела; k -жесткость пружины. Период колебаний математического маятника
где l - длина маятника; g - ускорение свободного падения. Период колебаний физического маятника
где J - момент инерции колеблющегося тела относительно оси колебаний; а - расстояние центра масс маятника от оси колебаний. Период крутильных колебаний тела, подвешенного на упругой нити,
где J - момент инерции тела относительно оси, совпадающей с упругой нитью; k - жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается. Уравнение затухающих колебаний
где А(t) - амплитуда затухающих колебаний в момент t; ω – их круговая частота. Угловая частота затухающих колебаний
где δ – коэффициент затухания. Зависимость амплитуды затухающих колебаний от времени
где А0 - амплитуда колебаний в момент t=0. Логарифмический декремент затухания
Амплитуда вынужденных колебаний
где F0 - амплитудное значение вынуждающей силы. Резонансная частота и резонансная амплитуда вынужденных колебаний
|
|
 , действующей на тело, относительно оси вращения
, действующей на тело, относительно оси вращения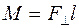 ,
, - проекция силы
- проекция силы  ,
,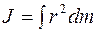
 ,
, .
. ,
, - момент импульса i-го тела, входящего в состав системы.
- момент импульса i-го тела, входящего в состав системы.
 mR2
mR2



 - моменты инерции и угловые скорости тел до взаимодействия;
- моменты инерции и угловые скорости тел до взаимодействия;  - те же величины после взаимодействия.
- те же величины после взаимодействия. ,
,
 - момент силы, действующей на тело в течение времени dt;J - момент инерции тела;ω - угловая скорость;
- момент силы, действующей на тело в течение времени dt;J - момент инерции тела;ω - угловая скорость;  - момент импульса.
- момент импульса.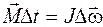 .
. ,
, .
.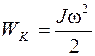 .
.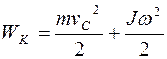 ,
, - кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр масс.
- кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр масс. ,
, ,
, ,
, ,
, , то
, то .
.
 ,
, ,
, , или
, или  ,
, , или
, или  ,
, ,
,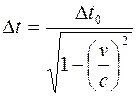 ,
,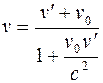 ,
, , или
, или  ,
, ).
). , или
, или  ,
, ,
, - кинетическая энергия частицы;
- кинетическая энергия частицы;  - ее энергия покоя.
- ее энергия покоя.

 ,
,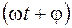 - фаза колебаний в момент t.
- фаза колебаний в момент t.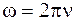 , или
, или 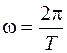 ,
,
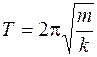 ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, .
. ,
, и
и  .
.