|
|
Выход акустической волны на границу раздела жидкость – воздух.Прежде всего рассмотрим в каких случаях возможно перемещение предметов, находящихся в жидкости под действием ударной или акустической волны. Если предмет находится на пути распространения подводной ударной волны на значительном расстоянии от границы жидкость – воздух, то при малом сечении предмета его перемещение будет незначительным. Иначе обстоит дело в случае нахождения того же предмета вблизи границы раздела жидкость – газ . При достижении ударной волной границы жидкость – газ, в газ выйдет преломлённая волна сжатия , а по жидкости будет распространяться волна разрежения. Когда волна разрежения создаст в жидкости на глубине h напряжение растяжения , превышающее сумму гидростатического давления на этой глубине и динамической прочности жидкости на разрыв, произойдёт кавитационный разрыв сплошности жидкости. Если граница жидкость – воздух находится на уровне верхнего фланца устьевой арматуры или открытой перфораторной задвижки , то кавитационный разрыв сплошности будет сопровождаться выбросом части оторванного слоя жидкости из скважины. В случае нахождения предмета в оторванном слое и отсутствия якорящих устройств предмет может быть увлечён жидкостью и выброшен из скважины. За первым разрывом сплошности жидкости последуют другие разрывы и процесс продолжится до тех пор, пока в скважинной жидкости будут возникать достаточные растягивающие напряжения, которые зависят от формы волны. Роль свободной поверхности, на которой происходит скачёк акустического сопротивления, при втором и последующих разрывах будут играть предыдущие кавитационные разрывы. Понятно, что давление на границе кавитационного разрыва близко к нулю. Менее определённой является динамическая прочность жидкости на разрыв. По экспериментальным данным Бриджа вода, свободная от механических примесей и газовых включений, выдерживает давление на разрыв в десятки МПа. Поскольку разрывы в скважинной жидкости не достигают глубины в сотни метров гидростатическим давлением на уровне кавитационного разрыва можно пренебречь и учитывать только прочность жидкости на разрыв. Для получения принципиальных соотношений рассмотрим упрощённую задачу. Пусть на поверхность раздела падает плоская волна экспоненциального профиля:
где Применив метод зеркального отображения источника и стока, найдём результирующее давление на глубине
где а0 – скорость звука в скважинной жидкости. Приравнивая результирующее давление из 9.19 прочности жидкости на разрыв -
Из (9.20) получим выражение для толщины первого выброшенного слоя жидкости:
Рассмотрим движение первого оторванного слоя . В нулевом приближении (пренебрегая сопротивлением воздуха) движение этого слоя тормозится силой тяжести. Поэтому дифференциальное уравнение движения запишется в следующем виде.
где При достаточно большой общей массе зарядов и отсутствии газовых включений в скважинной жидкости величина h1 может составлять сотни метров. Движение столба скважинной жидкости выше зоны разрыва вверх и даже частичный выброс её из скважины приведёт к возникновению временной депрессии на пласт и поступлению из последнего пластового флюида в скважину. Для газовых скважин или нефтяных, эксплуатирующих пласты с большим газовым фактором, это может привести к поступлению в скважину газа и несанкционированному фонтанированию. |
|
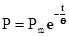 , (4.6)
, (4.6) - давление на фронте волны; t –текущее время, отсчитанное от фронта волны;
- давление на фронте волны; t –текущее время, отсчитанное от фронта волны; 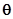 - показатель падения давления в волне.
- показатель падения давления в волне.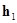 (см Рис. 4.19)
(см Рис. 4.19) (4.7),
(4.7), к получим
к получим
 (4.8)
(4.8) (9.21)
(9.21)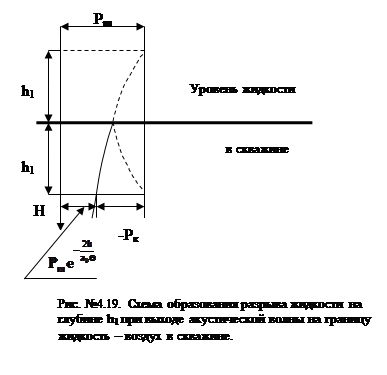 Из представленной зависимости следует, что глубина разрыва сплошности жидкости h1 в скважине зависит не от абсолютного значения давления на фронте волны Рm , но определяется относительной прочностью воды на разрыв. Чем ближе значения Рm и PК , тем на большей глубине будет происходить образование кавитационнной полости. Значительное влияние на глубину разрыва h1 оказывает показатель падения давления в волне
Из представленной зависимости следует, что глубина разрыва сплошности жидкости h1 в скважине зависит не от абсолютного значения давления на фронте волны Рm , но определяется относительной прочностью воды на разрыв. Чем ближе значения Рm и PК , тем на большей глубине будет происходить образование кавитационнной полости. Значительное влияние на глубину разрыва h1 оказывает показатель падения давления в волне  зависит от количества и общей массы одновременно срабатывающих в скважине кумулятивных зарядов.
зависит от количества и общей массы одновременно срабатывающих в скважине кумулятивных зарядов. , (4.10)
, (4.10)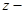 вертикальная координата,
вертикальная координата,  - плотность воды.
- плотность воды.